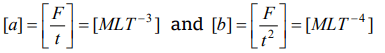1. Let \[\left(\epsilon_{0}\right)\] denotes the dimensional formula of the permittivity of the vacuum and \[\left(\mu_{0}\right)\] that of the
permeability of the vacuum. If M = mass, L = lenth, T = time and l = electric current, then
a) \[\left[\epsilon_{0}\right]=M^{-1}L^{-3}T^{2}I\]
b) \[\left[\epsilon_{0}\right]=M^{-1}L^{-3}T^{4}I^{2}\]
c) \[\left[\mu_{0}\right]=MLT^{-2}I^{-2}\]
d) Both b and c
Explanation: Both b and c
2. Dimensions of CR are those of
a) Frequency
b) Energy
c) Time period
d) Current
Explanation:
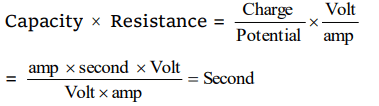
3. The physical quantity that has no dimensions
a) Angular Velocity
b) Linear momentum
c) Angular momentum
d) Strain
Explanation: Strain has no dimensions
4. \[ML^{-1}T^{-2}\] represents
a) Stress
b) Young's Modulus
c) Pressure
d) All the above three quantities
Explanation: All the above three quantities
5. Dimensions of magnetic field intensity is
a) \[M^{0}L^{-1}T^{0}A^{1}\]
b) \[MLT^{-1}A^{-1}\]
c) \[ML^{0}T^{-2}A^{-1}\]
d) \[MLT^{-2}A\]
Explanation:
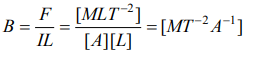
6. The force F on a sphere of radius \['a'\] moving in a medium with velocity 'v' is given by \[F=6\pi\eta av\] . The dimensions of \[\eta\] are
a) \[ML^{-1}T^{-1}\]
b) \[MT^{-1}\]
c) \[MLT^{-2}\]
d) \[ML^{-3}\]
Explanation:
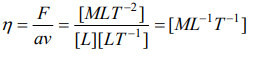
7. Which physical quantities have the same dimension
a) Couple of force and work
b) Force and power
c) Latent heat and specific heat
d) Work and power
Explanation:
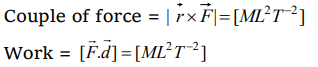
8. Two quantities A and B have different dimensions. Which mathematical operation given below is physically meaningful
a) \[A\diagup B\]
b) \[A+ B\]
c) \[A- B\]
d) None
Explanation: Quantities having different dimensions can only be divided or multiplied but they cannot be added or subtracted.
9. The physical quantity which has the dimensional formula \[M^{1}T^{-3}\] is
a) Surface tension
b) Solar constant
c) Density
d) Compressibility
Explanation:
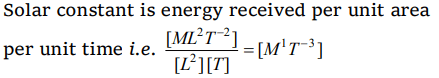
10. A force F is given by \[F=at+bt^{2}\] where t is time. What are the dimensions of a and b
a) \[MLT^{-3}\] and \[ML^{2}T^{-4}\]
b) \[MLT^{-3}\] and \[MLT^{-4}\]
c) \[MLT^{-1}\] and \[MLT^{0}\]
d) \[MLT^{-4}\] and \[MLT^{1}\]
Explanation: From the principle of dimensional homogenity