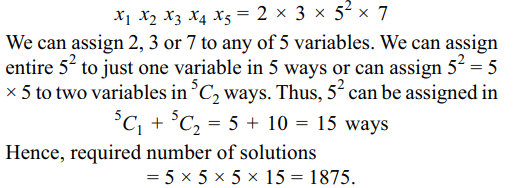1. Number of solutions of \[2x^{\left(x!+x\right)}=\left(x!+x\right)^{x},x\epsilon N\]
is
a) 0
b) 1
c) 2
d) infinite
Explanation: For x \[\epsilon\] N, we can write the given equation as
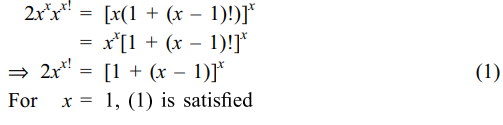
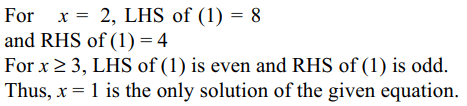
2. Let n = 2019. The least positive integer k
for which
\[k\left(n^{2}\right)\left(n^{2}-1^{2}\right)\left(n^{2}-2^{2}\right)\left(n^{2}-3^{2}\right)....\left(n^{2}-\left(n-1\right)^{2}\right)=r!\]
for some positive integer r is
a) 2019
b) 2018
c) 1
d) 2
Explanation: We can rewrite the given expression as
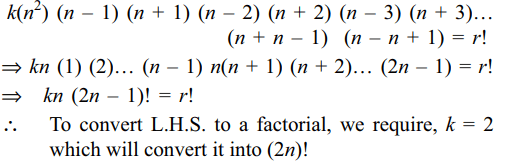
3. If \[0< r < s\leq n\] and \[^{n}P_{r}=^{n}P_{s}\] , then value of
r + s is
a) 2n – 2
b) 2n – 1
c) 2
d) 1
Explanation:
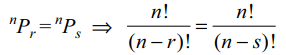
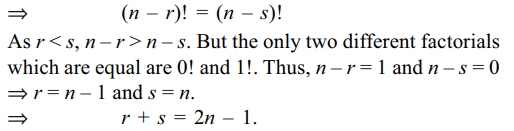
4. if \[\frac{1}{4}.\frac{2}{6}.\frac{3}{8}.\frac{4}{10}....\frac{30}{62}.\frac{31}{64}=8^{x}\]
then value of x is
a) -7
b) -9
c) -10
d) -12
Explanation:
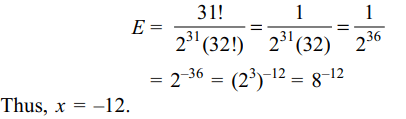
5. The sum\[\sum_{i=0}^{m}\left(\begin{array}{c}10\\ i\end{array}\right)\left(\begin{array}{c}20\\ m-i\end{array}\right)\]
(where \[\left(\begin{array}{c}p\\ q\end{array}\right)=0\] if (p < q) is maximum where m is
a) 5
b) 10
c) 15
d) 20
Explanation:
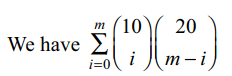
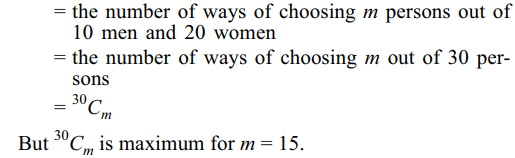
6. Let \[T_{n}\] denote the number of triangles
which can be formed by using the vertices of a regular
polygon of n sides. If \[T_{n+1}-T_{n}=21\] , then n equals
a) 5
b) 7
c) 6
d) 4
Explanation: The number of triangles that can be formed by
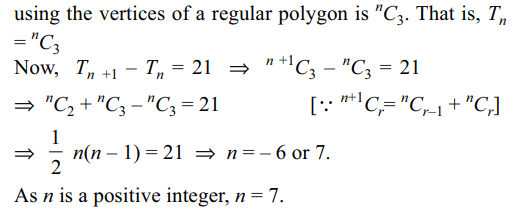
7. An eight digits number divisible by 9 is
to be formed by using 8 digits out of the digits 0, 1, 2, 3, 4,
5, 6, 7, 8, 9 without replacement. The number of ways in
which this can be done is
a) 9!
b) 2(7!)
c) 4(7!)
d) (36) (7!)
Explanation: We have 0 + 1 + 2 + 3 … + 8 + 9 = 45
To obtain an eight digits number exactly divisible by 9, we must not use either (0, 9) or (1, 8) or (2, 7) or (3, 6) or (4, 5). [Sum of the remaining eight digits is 36 which is exactly divisible by 9].
When, we do not use (0, 9), then the number of required 8 digit number is 8!.
When one of (1, 8) or (2, 7) or (3, 6) or (4, 5) is not used, the remaining digits can be arranged in 8! – 7! ways as 0 cannot be at extreme left.
Hence, there are 8! + 4(8! – 7!) = (36) (7!) numbers in the desired category
8. The number of rational numbers lying in
the interval (2018, 2019) all whose digits after the decimal
point are non-zero and are in decreasing order is
a) \[\sum_{i=1}^{9}\] \[^{9}P_{i}\]
b) \[\sum_{i=1}^{10}\] \[^{9}P_{i}\]
c) \[2^{9}-1\]
d) \[2^{10}-1\]
Explanation: A rational number of the desired category
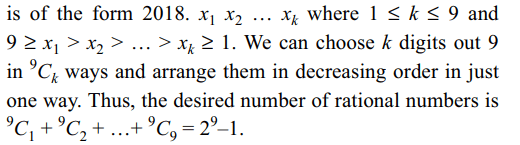
9. The number of functions f from the set A
= {0, 1, 2} in to the set B = {0, 1, 2, 3, 4, 5, 6, 7} such that
\[f\left(i\right)\leq f\left(j\right)\] for i < j and \[i,j \epsilon A\] is
a) \[^{8}C_{3}\]
b) \[^{8}C_{3}+2\left(^{8}C_{2}\right)\]
c) \[^{10}C_{3}\]
d) \[^{9}C_{3}\]
Explanation:
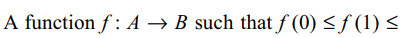

10. The number of positive integral solutions
of the equation \[x_{1}x_{2}x_{3}x_{4}x_{5}=1050\] is
a) 1800
b) 1675
c) 1400
d) 1875
Explanation: Using prime-factorization of 1050, we can write the given equation as