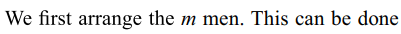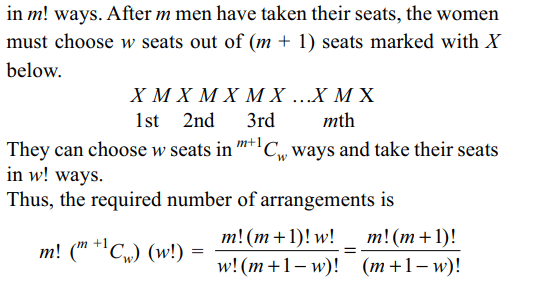1. The exponent of 7 in \[^{100}C_{50}\] is
a) 0
b) 2
c) 3
d) 4
Explanation:
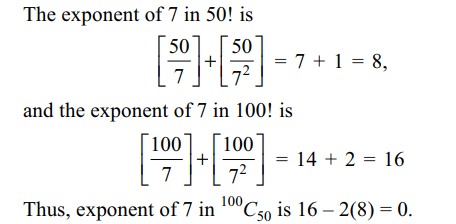
2. In a certain test there are n questions.
In this test \[2^{k}\] students gave wrong answers to at least
(n – k) questions, where k = 0, 1, 2, …, n. If the total
number of wrong answers is 4095, then value of n is
a) 11
b) 12
c) 13
d) 15
Explanation: The number of students answering at least r
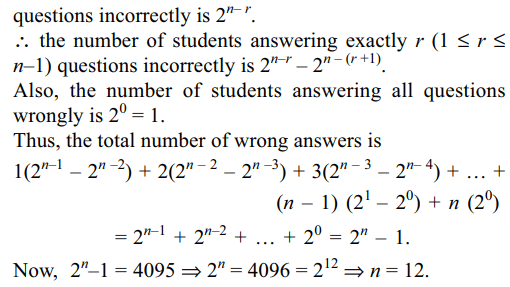
3.If n > 1 and n divides (n – 1)! + 1, then
a) n must be prime
b) n must be divisible by exactly two primes
c) n must be a composite number
d) n must be divisible by \[p^{2}\] where p is primes
Explanation: If n is not prime, then there exists r ∈ N such
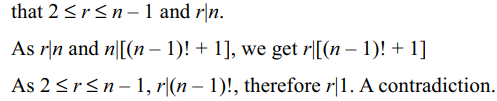
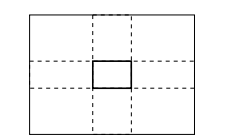
4. A \[11\times11\] grid is divided into five
rectangles along the grid. The number of ways to divide
the grid into five rectangles so that one of the rectangles
generated by the division doesn’t have any edge on the
periphery is
a) 32400
b) 16200
c) 14000
d) 18000
Explanation: There are 12 horizontal and 12 vertical lines on a 11 * 11 grid.

5. For \[n\geq 2\] , let \[\alpha= \sum_{r=1}^{n}r!\sum_{s=1}^{n}s!\sqrt{s}\log_{10}\left(s\right)\]
and \[\beta=\sum_{r=1}^{n}r!\sqrt{r}\sum_{s=1}^{n}s!\log_{10}\left(s\right)\] , then
a) \[\alpha=\beta\]
b) \[\alpha\beta=1\]
c) \[\alpha>\beta\]
d) \[\alpha<\beta\]
Explanation:

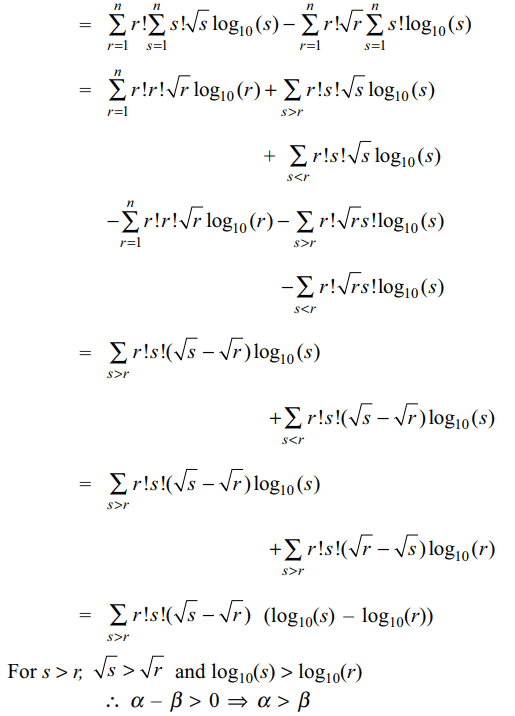
6. Sum of the series\[\sum_{r=1}^{n}\left(r^{2}+1\right)\left(r!\right)\]
is
a) \[\left(n+1\right)!\]
b) \[\left(n+2\right)!-1\]
c) \[n\left(n+1\right)!\]
d) \[n\left(n+2\right)!\]
Explanation:
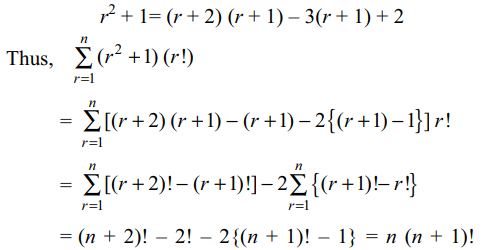
7. In a group of 8 girls, two girls are sisters.
The number of ways in which the girls can sit so that two
sisters are not sitting together is
a) 48200
b) 14100
c) 28300
d) 30240
Explanation: The required number of ways = the number of ways in which 8 girls can sit – the number of ways in which two sisters are together
= 8! – (2) (7!) = 30240.
8.The number of words that can be formed
by using the letters of the word MATHEMATICS that start
as well as end with T is
a) 80720
b) 90720
c) 20860
d) 37528
Explanation: The word MATHEMATICS contains 11 letters viz. M, M, A, A, T, T, H, E, I, C, S. The number of words that begin with T and end with T is
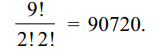
9. If \[a_{n}=\sum_{r=0}^{n}\frac{1}{^{n}C_{r}}\] , then
\[\sum_{r=0}^{n}\frac{r}{^{n}C_{r}}\] equals
a) \[\frac{n}{2}a_{n}\]
b) \[\frac{n}{4}a_{n}\]
c) \[na_{n}\]
d) \[\left(n-1\right)a_{n}\]
Explanation:
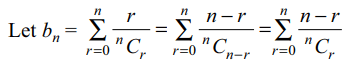
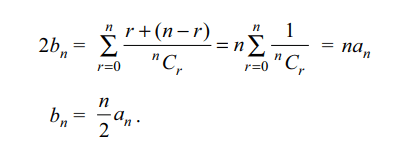
10. m men and w women are to be seated in a
row so that no two women sit together. If m > w, then the
number of ways in which they can be seated is
a) \[\frac{m!\left(m+1\right)!}{\left(m-w+1\right)!}\]
b) \[^{m}C_{m-w}\left(m-w\right)!\]
c) \[^{m+w}C_{m}\left(m-w\right)!\]
d) none of these
Explanation: