1. The number of ways of arranging letters
of the word RACHIT so that the vowels are in alphabetical
order is
a) 120
b) 240
c) 360
d) 480
Explanation: We can arrange letters of the word RACHIT in 6! ways. Out of these exactly half, that is, there are
2. if \[^{n-1}C_{r}=\left(K^{2}-3\right)\left(^{n}C_{r+1}\right)\] then K belong to
a) \[\left[-\sqrt{3},\sqrt{3}\right]\]
b) \[\left(-\infty,-2\right)\]
c) (2, \[\infty\] )
d) \[(\sqrt{3}\] ,2]
Explanation:

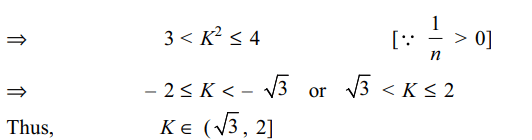
3. A five digit number divisible by 3 is to be formed using the numerals 0, 1, 2, 3, 4 and 5 without
repetition. The total number of ways in which this can be
done is
a) 216
b) 240
c) 600
d) 3125
Explanation: The sum of the numerals 0, 1, 2, 3, 4 and 5 is

4. The number of ways in which a mixed
double game can be arranged from amongst 9 married
couples if no husband and wife play in the same game is
a) 756
b) 1512
c) 3024
d) 378
Explanation: We can choose two men out of 9 in \[^{9}C_{2}\] ways
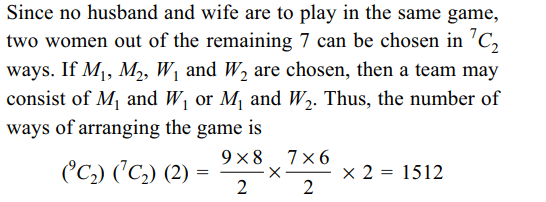
5. The sum of the divisors of \[2^{5}.3^{7}.5^{3}.7^{2}\] is
a) \[2^{6}.3^{8}.5^{4}.7^{3}\]
b) \[2^{6}.3^{8}.5^{4}.7^{3}-2.3.5.7\]
c) \[2^{6}.3^{8}.5^{4}.7^{3}-1\]
d) none of these
Explanation: Any divisor of 25 . 37 . 53 . 72 is of the form
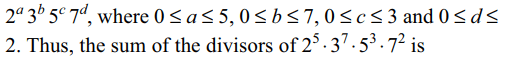
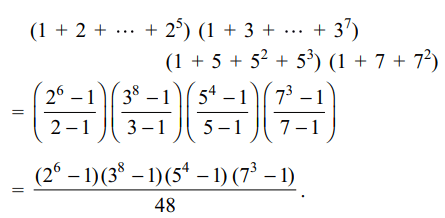
6. The number of times the digit 3 will be
written when listing the integers from 1 to 1000 is
a) 269
b) 300
c) 271
d) 302
Explanation: Since 3 does not occur in 1000, we have to

7. The number of positive integers n such
that \[2^{n}\] divides n! is
a) exactly 1
b) exactly 2
c) infinite
d) none of these
Explanation: The exponent of 2 in n! is given by
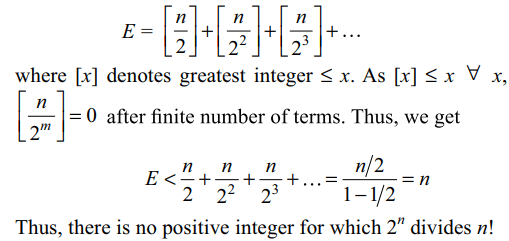
8. The sum\[\sum\sum_{0\leq i< j\leq 10}\left(^{10}C_{j}\right)\left(^{j}C_{i}\right)\] is equal to
a) \[2^{10}-1\]
b) \[2^{10}\]
c) \[3^{10}-1\]
d) \[3^{10}\]
Explanation:
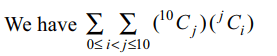
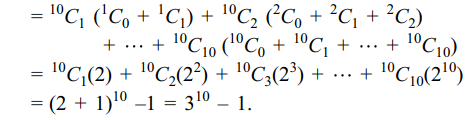
9. A class contains 4 boys and g girls. Every sunday five students , including at least three boys go for
a picnic to Appu Ghar, a different group being sent every
week. During, the picnic, the class teacher gives each girl
in the group a doll. If the total number of dolls distributed
was 85, then value of g is
a) 15
b) 12
c) 8
d) 5
Explanation: Number of groups having 4 boys and 1 girl
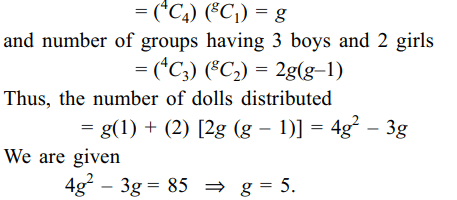
10. The largest three digit prime number
dividing \[^{2000}C_{1000}\] is
a) 661
b) 659
c) 673
d) 681
Explanation: