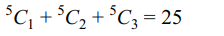1. The letters of the word SURITI are written in all
possible orders and these words are written out as in
a dictionary. Then the rank of the word SURITI is
a) 224
b) 245
c) 307
d) 315
Explanation:

2. A candidate is required to answer 6 out of 10
questions which are divided into two groups, each
containing 5 questions. He is not permitted to
attempt more than 4 questions from either group.
The number of different ways in which the candidate
can choose six questions is
a) 50
b) 150
c) 200
d) 250
Explanation:

3. Let A = {1, 2, 3 .... n}, B = {a, b, c}, then the number
of functions from A to B that are onto is
a) \[ 3^{n}-3\left(2^{n}-1\right)\]
b) \[ 3^{n}-2^{n}\]
c) \[ 3\left(2^{n}-1\right)\]
d) (n – 1)!
Explanation:
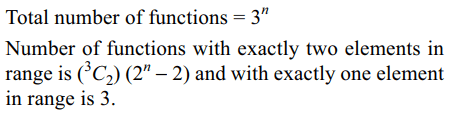
4. If \[\alpha=^{m}C_{2}\] , where m ≥ 2, then the value of \[^{\alpha}C_{2}\] is
given by
a) \[^{m+1}C_{4}\]
b) \[^{m-1}C_{4}\]
c) \[^{m+2}C_{4}\]
d) \[3\left(^{m+1}C_{4}\right)\]
Explanation:
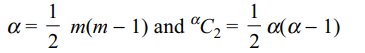
5. There are n white and n black balls marked 1, 2,
, ...., n. The number of ways in which we can arrange
these balls in a row so that neighbouring balls are of
different colours is
a) n!
b) (2n)!
c) \[2\left(n!\right)^{2}\]
d) \[\frac{\left(2n\right)!}{\left(n!\right)^{2}}\]
Explanation: The balls must be of alternate colours.
6. The number of squares which we can form on a
chessboard is
a) 64
b) 160
c) 224
d) 204
Explanation: For a square of size k × k, we have to choose (k + 1) consecutive horizontal and (k + 1) consecutive vertical lines from the chess board, and this can be done in (9 - k) × (9 - k) ways.
7. The number of 5 digit numbers that contain 7
exactly once is
a) \[\left(41\right)\left(9^{3}\right)\]
b) \[\left(37\right)\left(9^{3}\right)\]
c) \[\left(7\right)\left(9^{4}\right)\]
d) \[\left(41\right)\left(9^{4}\right)\]
Explanation:
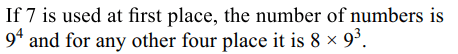
8. The units digit of \[17^{2009}+11^{2009}-7^{2009}\] is
a) 1
b) 8
c) 2
d) 9
Explanation:
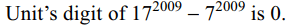
9. If \[\frac{1}{^{4}C_{n}}=\frac{1}{^{5}C_{n}}+\frac{1}{^{6}C_{n}}\] , then value of n is
a) 3
b) 4
c) 1
d) 2
Explanation:
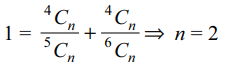
10. At an election there are five candidates and three members are to be elected, and a voter may vote
for any number of candidates not greater than the
number to be elected. The number of ways in which
the person can vote is
a) 25
b) 30
c) 35
d) \[2^{5}-2^{3}\]
Explanation: