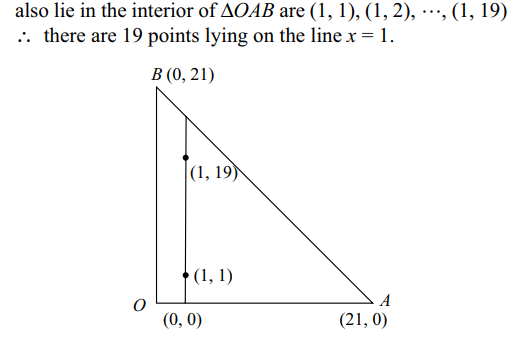1. The number of subsets of the set \[A=\left\{a_{1},a_{2},....a_{n}\right\}\] which contain even number of elements is
a) \[2^{n-1}\]
b) \[2^{n}-1\]
c) \[2^{n-2}\]
d) \[2^{n}\]
Explanation: For each of the first (n – 1) elements a1, a2,

2. The number of ways in which we can post
5 letters in 10 letter boxes is
a) 50
b) \[5^{10}\]
c) \[10^{5}\]
d) none of these
Explanation: We can post the first letter in 10 ways, the second letter in 10 ways and so on. Thus, the number of ways of posting 5 letters in 10 letter boxes is 10 * 10 * 10 * 10 * 10 = 105 .
3. The number of five digit telephone numbers having at least one of their digits repeated is
a) 90000
b) 10000
c) 30240
d) 69760
Explanation: The number of five digit telephone numbers which can be formed using the digits 0, 1, 2, .... , 9 is 105 (Refer to explanation of Q2). The number of five digit telephone numbers which have none of their digits repeated is \[^{10}P_{5}\] = 30240. Thus, the required number of telephone numbers is 105 – 30240 = 69760.
4. The ten’s digit of 1! + 2! + 3! + .... + 49! is
a) 1
b) 2
c) 3
d) 4
Explanation: We have 1! + 2! + 3! + 4! = 33. Also 5! = 120, 6! = 720, 7! = 5040, 8! = 40320 and 9! = 326880. Thus, the ten digits of 1! + 2! + .... + 9! is 1.
Also, note that n! is divisible by 100 for all n ≥ 10, so that ten’s digit of 10! + 11! + .... + 49! is zero. Therefore, ten’s digit of 1! + 2! + .... + 49! is 1.
5. Four dice are rolled. The number of
possible outcomes in which at least one die shows 2 is
a) 1296
b) 625
c) 671
d) 1023
Explanation: The total number of possible outcomes is 64 .
The number of possible outcomes in which 2 does not appear on any die is 54 . Therefore, the number of possible outcomes in which at least one die shows a 2 is 64 – 54 = 1296 – 625 = 671.
6. A set contains (2n + 1) elements. The
number of subsets of the set which contain at most n
elements is
a) \[2^{n}\]
b) \[2^{n+1}\]
c) \[2^{n-1}\]
d) \[2^{2n}\]
Explanation: Let N = the number of subsets of the set which contain at most n elements
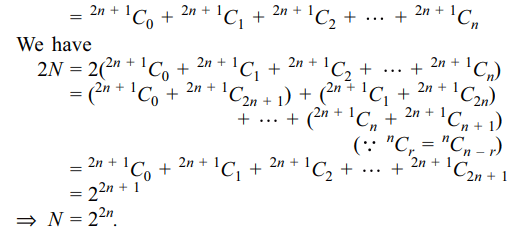
7. A is a set containing n elements. A subset
P of A is chosen. The set A is reconstructed by replacing the elements of P. A subset Q of A is again chosen. The
number of ways of choosing P and Q so that P \[\cap\] Q = \[\phi\] is
a) \[2^{2n}-^{2n}C_{n}\]
b) \[2^{n}\]
c) \[2^{n}-1\]
d) \[3^{n}\]
Explanation:
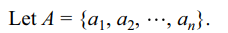
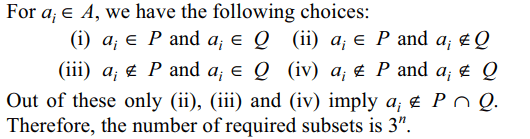
8. Let E = {1, 2, 3, 4} and F = {a, b}. Then
the number of onto functions from E to F is
a) 14
b) 16
c) 12
d) 32
Explanation: We first find the number of functions from E to F
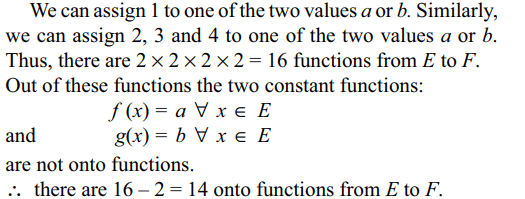
9. The number of ways of arranging letters of
the word HAVANA so that V and N do not appear together is
a) 40
b) 60
c) 80
d) 100
Explanation: We can arrange the letters H, A, A, A in
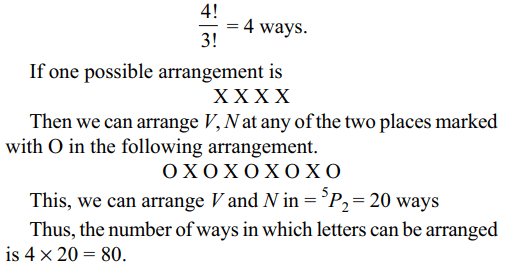
10. The number of integral points (integral
point means both the coordinates should be integer) that lie
exactly in the interior of the triangle with vertices.(0, 0), (0, 21), (21,0) is
a) 133
b) 190
c) 233
d) 105
Explanation: The integral points lying on the line x = 1 which