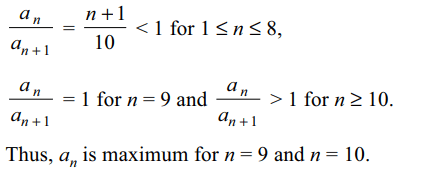1. If n is odd and \[^{n}C_{0}<^{n}C_{1}<^{n}C_{2}< ...<^{n}C_{r}\] , then
maximum possible value of r is
a) \[\frac{1}{2}\left(n+1\right)\]
b) \[\frac{1}{2}\left(n-1\right)\]
c) n
d) \[\frac{1}{3}\left(n+1\right)\]
Explanation:

2. The number of arrangements of the letters of the
word BANANA in which two N’s do not appear
adjacently is
a) 40
b) 60
c) 80
d) 100
Explanation:
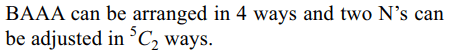
3. The number of positive integral solutions of
\[x_{1}x_{2}x_{3}x_{4}x_{5}=840\] is
a) 3125
b) 6125
c) 6250
d) 7250
Explanation:
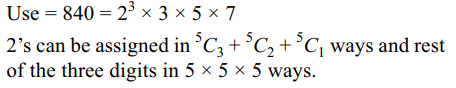
4. The number of ways we can put 5 different balls in
5 different boxes such that at most three boxes are
empty, is equal to
a) \[5^{5}+5\]
b) \[5^{5}-10\]
c) \[5^{5}-5\]
d) \[5^{5}-4^{5}\]
Explanation: Total number of ways - number of ways in which exactly four boxes remain empty
5. The number of ordered pairs of integers (x, y)
satisfying the equation \[x^{2}+6x+y^{2}=4\] is
a) 2
b) 4
c) 6
d) 8
Explanation:
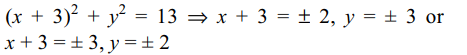
6. The number of the divisors of 20! is
a) 4140
b) 41040
c) 4204
d) 81650
Explanation:

7. The letters of the word COCHIN are permuted and
all the permutations are arranged in an alphabetical
order as in an English disctionary. The number of
words that appear before the word COCHIN is
a) 360
b) 192
c) 96
d) 48
Explanation: All the words beginning with CC, CH, CI and CN occur before COCHIN.
8. The number of five digit number that can be formed by using digits 1, 2, 3 only, such that exactly three
digit of the formed number are same, is
a) 30
b) 60
c) 90
d) none of these
Explanation:

9. The number of zeros at the end of 100! is
a) 20
b) 22
c) 24
d) 26
Explanation:

10. Let \[a_{n}=\frac{10^{n}}{n!}\] for n ≥ 1. Then \[a_{n}\] take the greatest
value when n is equal to
a) 9
b) 10
c) 11
d) Both a and b
Explanation: