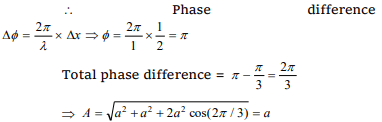1.Equation of a progressive wave is given by \[y = a\sin \pi\left[\frac{t}{2}-\frac{x}{4}\right]\] where t is in seconds and x is in
meters. The distance through which the wave
moves in 8 sec is (in meter)
a) 8
b) 16
c) 2
d) 4
Explanation:

2. A particle on the trough of a wave at any instant
will come to the mean position after a time (T =
time period)
a) T / 2
b) T / 4
c) T
d) 2T
Explanation:

3.If the equation of transverse wave is \[y = 2\sin \left(kx-2t\right)\] , then the maximum particle
velocity is
a) 4 units
b) 2 units
c) o
d) 6 units
Explanation:

4. There is a destructive interference between the
two waves of wavelength \[\lambda\] coming from two
different paths at a point. To get maximum sound
or constructive interference at that point, the
path of one wave is to be increased by
a) \[\frac{\lambda}{4}\]
b) \[\frac{\lambda}{2}\]
c) \[\frac{3\lambda}{4}\]
d) \[\lambda\]
Explanation:
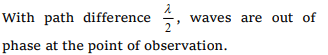
5. When two sound waves with a phase difference of \[\pi/2\] , and each having amplitude A and frequency \[\omega\] , are superimposed on each other, then the
maximum amplitude and frequency of resultant
wave is
a) \[\frac{A}{\sqrt{2}}:\frac{\omega}{2}\]
b) \[\frac{A}{\sqrt{2}}:\omega\]
c) \[\sqrt{2}A:\frac{\omega}{2}\]
d) \[\sqrt{2}A:\omega\]
Explanation:

6 If the phase difference between the two wave is
\[2\pi\] during superposition, then the resultant
amplitude is
a) Maximum
b) Minimum
c) Maximum or minimum
d) None of the above
Explanation: Phase difference is 2 \[\pi\] means constrictive interference so resultant amplitude will be maximum
7. The superposition takes place between two waves
of frequency f and amplitude a. The total intensity
is directly proportional to
a) a
b) 2a
c) \[2a^{2}\]
d) \[4a^{2}\]
Explanation:

8.If two waves of same frequency and same
amplitude respectively, on superimposition
produced a resultant disturbance of the same
amplitude, the waves differ in phase by
a) \[\pi\]
b) \[2 \pi/3\]
c) \[ \pi/2\]
d) Zero
Explanation:

9.Two sources of sound A and B produces the wave
of 350 Hz, they vibrate in the same phase. The
particle P is vibrating under the influence of these
two waves, if the amplitudes at the point P
produced by the two waves is 0.3 mm and 0.4
mm, then the resultant amplitude of the point P
will be when AP – BP = 25 cm and the velocity of
sound is 350 m/sec
a) 0.7 mm
b) 0.1 mm
c) 0.2 mm
d) 0.5 mm
Explanation:

10.Two waves are propagating to the point P along a
straight line produced by two sources A and B of
simple harmonic and of equal frequency. The amplitude of every wave at P is ‘a’ and the phase
of A is ahead by \[\frac{\pi}{3}\] than that of B and the distance
AP is greater than BP by 50 cm. Then the resultant
amplitude at the point P will be, if the wavelength
is 1 meter
a) 2a
b) \[a\sqrt{3}\]
c) \[a\sqrt{2}\]
d) a
Explanation: