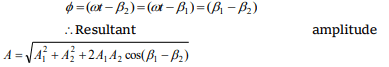PrepBharat

1.Coherent sources are characterized by the same
a) Phase and phase velocity
b) Wavelength, amplitude and phase velocity
c) Wavelength, amplitude and frequency
d) Both b and c

View Answer

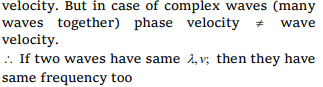
2. The minimum intensity of sound is zero at a point due to two sources of nearly equal frequencies, when
a) Two sources are vibrating in opposite phase
b) The amplitude of two sources are equal
c) At the point of observation, the amplitudes of two S.H.M. produced by two sources are equal and both the S.H.M. are along the same straight line
d) Both the sources are in the same phase

View Answer

3.Two sound waves (expressed in CGS units) given by \[y_{1}=0.3\sin\frac{2\pi}{\lambda}\left(vt-x\right)\]
and \[y_{2}=0.4\sin\frac{2\pi}{\lambda}\left(vt-x+\theta\right)\]
interfere. The resultant amplitude at a place where phase difference is \[\pi/ 2\]  will be
a) 0.7 cm
b) 0.1 cm
c) 0.5 cm
d) \[\frac{1}{10}\sqrt{7}\]   cm

View Answer

4. If two waves having amplitudes 2A and A and same frequency and velocity, propagate in the same direction in the same phase, the resulting amplitude will be
a) 3A
b) \[\sqrt{5}A\]
c) \[\sqrt{2}A\]
d) A

View Answer

5. The intensity ratio of two waves is 1 : 16. The ratio of their amplitudes is
a) 1 : 16
b) 1 : 4
c) 4 : 1
d) 2 : 1

View Answer

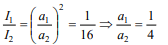
6. Out of the given four waves (1), (2), (3) and (4)
\[y= a\sin\left(kx+\omega t\right)\]       ......(1)
\[y= a\sin\left(\omega t-kx\right)\]       ......(2)
\[y= a\cos\left(kx+\omega t\right)\]       ......(3)
\[y= a\cos\left(\omega t-kx\right)\]       ......(4)
emitted by four different sources S₁ , S₂ , S₃ and S₄ respectively, interference phenomena would be observed in space under appropriate conditions when
a) Source \[S_{1}\]  emits wave (1) and \[S_{2}\]  emits wave (2)
b) Source \[S_{3}\]  emits wave (3) and \[S_{4}\]  emits wave (4)
c) Source \[S_{2}\]  emits wave (2) and \[S_{4}\]  emits wave (4)
d) \[S_{4}\]  emits waves (4) and \[S_{3}\]  emits waves (3)

View Answer

7. Two waves of same frequency and intensity superimpose with each other in opposite phases, then after superposition the
a) Intensity increases by 4 times
b) Intensity increases by two times
c) Frequency increases by 4 times
d) None of these

View Answer

8.The superposing waves are represented by the following equations :
\[y_{1}= 5\sin2\pi\left(10 t-0.1 x\right),y_{2}= 10\sin2\pi\left(20 t-0.2 x\right)\]
Ratio of intensities \[\frac{I_{max}}{I_{min}}\]   will be
a) 1
b) 9
c) 4
d) 16

View Answer

9.The displacement of a particle is given by
\[y= 3\sin\left(5\pi t\right)+4\cos\left(5\pi t\right)\]
The amplitude of the particle is
a) 3
b) 4
c) 5
d) 7

View Answer

10.Two waves
\[y_{1}= A_{1}\sin\left(\omega t-\beta_{1}\right) ,y_{2}= A_{2}\sin\left(\omega t-\beta_{2}\right) \]
Superimpose to form a resultant wave whose amplitude is
a) \[\sqrt{A_1^2+A_2^2+2A_{1}A_{2} \cos\left(\beta_{1}-\beta_{2}\right)}\]
b) \[\sqrt{A_1^2+A_2^2+2A_{1}A_{2} \sin\left(\beta_{1}-\beta_{2}\right)}\]
c) \[A_{1}+A_{2}\]
d) \[\mid A_{1}+A_{2} \mid\]

View Answer