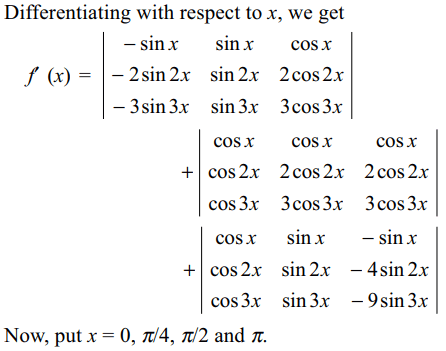PrepBharat

1. Suppose a, b, c are distinct non-zero real numbers and
\[\triangle_{1}=\begin{bmatrix}a^{2} & b^{2} & c^{2} \\b^{2}+c^{2} & c^{2}+a^{2} & a^{2}+b^{2} \\bc & ca & ab\end{bmatrix}\]
and \[\triangle_{2}=\begin{bmatrix}1 & a & a^{3} \\1 & b & b^{3} \\1 & c & c^{3}\end{bmatrix}\]
then \[\frac{\triangle_{2}-\triangle_{1}}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\]         is equal to
a) a + b + c
b) \[a^{2}+b^{2}+c^{2}\]
c) \[\left(a+b+c\right)\left(1+a^{2}+b^{2}+c^{2}\right)\]
d) \[4\left(abc\right)^{2}\]

View Answer

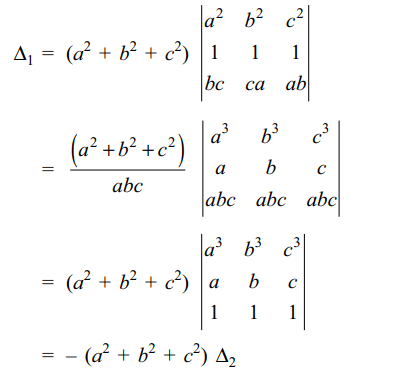
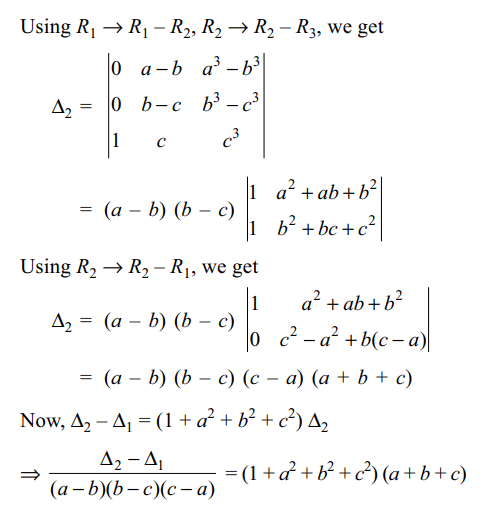
2. Let \[\omega=-\frac{1}{2}+\frac{i\sqrt{3}}{2}\]     . Then the value of the determinant \[\triangle=\begin{bmatrix}1 & 1 & 1 \\1 & -1-\omega^{2} & \omega^{2} \\1 &\omega^{2} & \omega^{4}\end{bmatrix}\]
is
a) \[3\omega\]
b) \[3\omega\left(\omega-1\right)\]
c) \[3\omega^{2}\]
d) \[3\omega\left(1-\omega\right)\]

View Answer

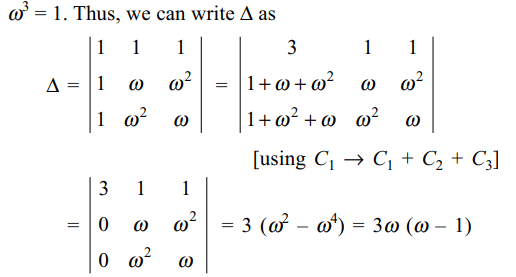
3. if \[n\epsilon N\] and \[A=\begin{bmatrix}n! & \left(n+1\right)! & \left(n+2\right)! \\\left(n+1\right)! & \left(n+2\right)! & \left(n+3\right)! \\\left(n+2\right)! & \left(n+3\right)! & \left(n+4\right)!\end{bmatrix}\]
then \[\lim_{n \rightarrow \infty}\frac{\left(3n^{3}-5\right)\triangle_{n}}{\triangle_{n+1}}\]     equal
a) \[\frac{3}{2}\]
b) \[\frac{5}{2}\]
c) \[-\frac{5}{2}\]
d) 3

View Answer

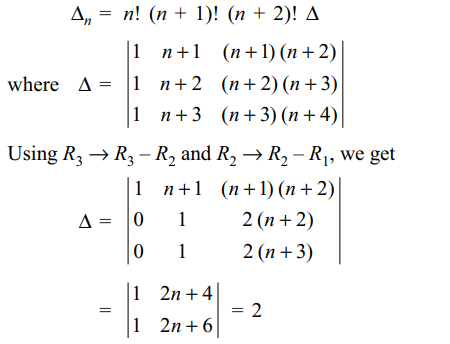
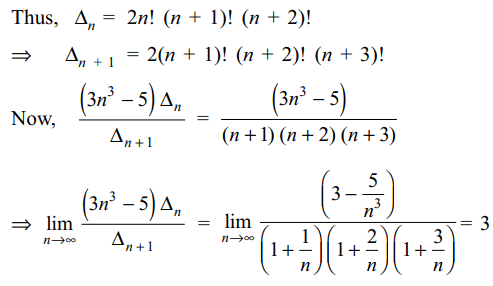
4. If \[f(x)=\begin{bmatrix}1 & x & x+1 \\2x & x\left(x-1\right) & \left(x+1\right)x \\3x\left(x-1\right) & x\left(x-1\right)\left(x-2\right) & \left(x+1\right)x\left(x-1\right)\end{bmatrix}\]
then f(2018) is equal to
a) 0
b) 1
c) 2018
d) 2019

View Answer

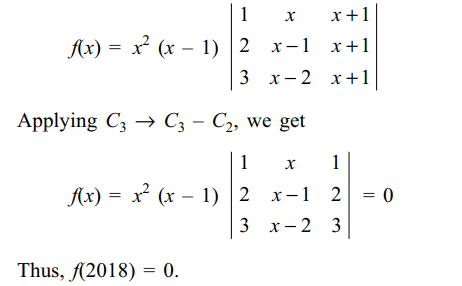
5. The number of positive integral solutions of the equation Δ = 12, where \[\triangle=\begin{bmatrix}y+z & z & y \\z & z+x & x \\y & x & x+y\end{bmatrix}\]
is
a) 3
b) 15
c) 4
d) \[2^{3}3^{2}\]

View Answer

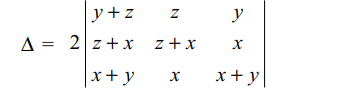
6. If \[a_{1},a_{2},a_{3},.......,a_{9}\]     are in H.P. and \[a_{4}=5,a_{5}=4\]   , then value of the determinant
\[\triangle=\begin{bmatrix}a_{1} & a_{2} & a_{3} \\a_{4} & a_{5} & a_{6} \\a_{7} & a_{8} & a_{9}\end{bmatrix}\]
equals
a) \[\frac{1}{20}\]
b) \[\frac{50}{21}\]
c) \[\frac{3}{20}\]
d) \[\frac{7}{90}\]

View Answer

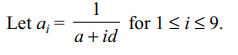
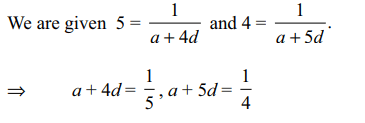
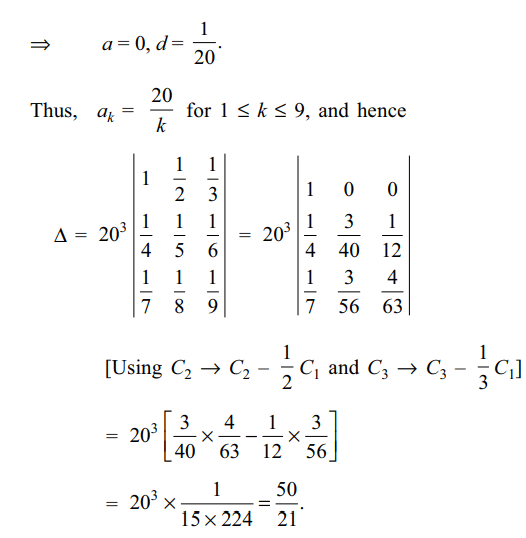
7. Let \[\omega\] be the complex number \[\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\]     Then the number of distinct complex number z satisfying
\[\triangle=\begin{bmatrix}z+1 & \omega & \omega^{2} \\\omega & z+\omega^{2} & 1 \\\omega^{2} & 1 & z+\omega\end{bmatrix} = 0\]
is
a) 1
b) 2
c) 3
d) infinte

View Answer

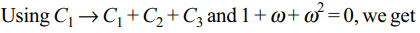
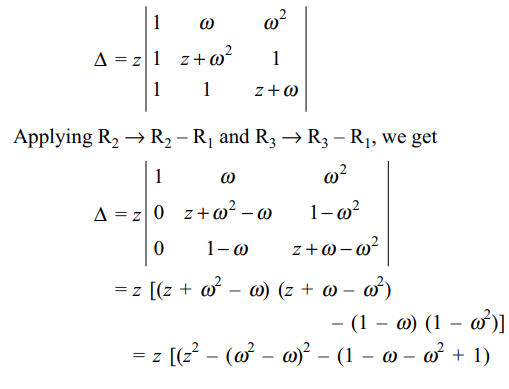
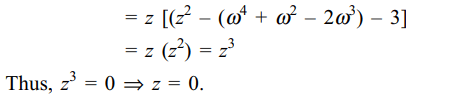
8. If a, b, c are three complex number such that \[a^{2}+b^{2}+c^{2}=0\]     and
\[\triangle=\begin{bmatrix}b^{2}+c^{2} & ab & ac \\ab & c^{2}+a^{2} & bc \\ac & bc & a^{2}+b^{2}\end{bmatrix}=ka^{2}b^{2}c^{2} ,\]
then value of k is
a) 1
b) 2
c) -2
d) 4

View Answer

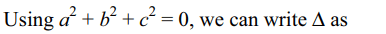
9. The determinant \[\triangle=\begin{bmatrix}a^{2} & a & 1 \\\cos\left(nx\right) & \cos\left(n+1\right) x &\cos\left(n+2\right)x \\sin\left(nx\right) & \sin\left(n+1\right)x & \sin\left(n+2\right)x \end{bmatrix}\]
is independent of
a) n
b) x
c) a
d) none of these

View Answer

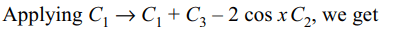
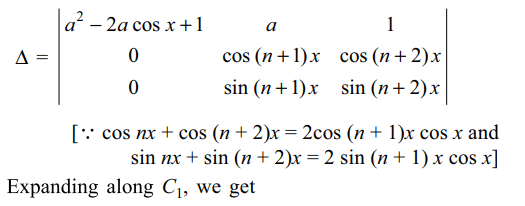
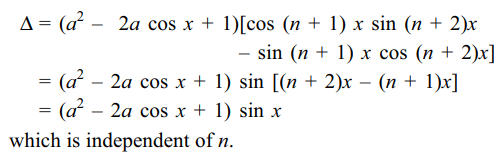
10. Suppose \[n\epsilon N\]  and \[1\leq r\leq n-3\]    and
\[\triangle\left(n,r\right)=\begin{bmatrix}^{n}C_{r-1} & ^{n}C_{r} & \left(r+1\right) \left(^{n+2}C_{r+1}\right)\\^{n}C_{r} & ^{n}C_{r+1} &\left(r+2\right) \left(^{n+2}C_{r+2}\right) \\^{n}C_{r+1} & ^{n}C_{r+2} & \left(r+3\right) \left(^{n+2}C_{r+3}\right) \end{bmatrix}\]
then \[\triangle\left(n,r\right)\]   is equal to
a) 0
b) n! – r!
c) \[^{n+4}C_{r+3}\]
d) \[^{n+4}C_{r+4}\]

View Answer

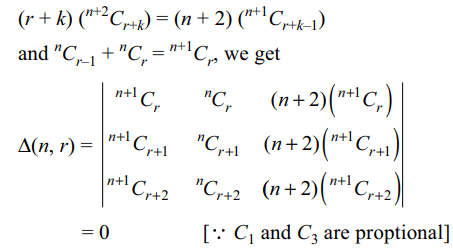
11. If a, b, c are non-zero real numbers, then \[\triangle=\begin{bmatrix}1 & ab &\frac{1}{a}+\frac{1}{b} \\1 & bc & \frac{1}{b}+\frac{1}{c} \\1 & ca & \frac{1}{c}+\frac{1}{a}\end{bmatrix}\]
is
a) 0
b) bc + ca + ab
c) \[a^{-1}+b^{-1}+c^{-1}\]
d) none of these

View Answer

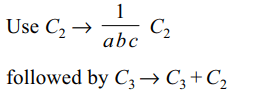
12. If a, b, c > 1 , \[\triangle=\begin{bmatrix}\log_{a}\left(abc\right) & \log_{a}b &\log_{a}c \\\log_{b}\left(abc\right) & 1 & \log_{b}c \\\log_{c}\left(abc\right) & \log_{c}b & 1\end{bmatrix}\]
is
a) 0
b) \[ \log_{a}b+ \log_{b}c+ \log_{c}a\]
c) \[ \log_{abc}\left(a+b+c\right)\]
d) 3

View Answer

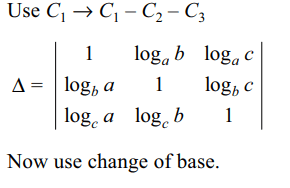
13. If a, b, c are positive and are the pth, qth and rth terms respectively of a G.P., then \[ \triangle=\begin{bmatrix}\log a & p & 1 \\\log b & q & 1 \\\log c & r & 1\end{bmatrix}\]
is
a) 0
b) log (abc)
c) – (p + q + r)
d) 3

View Answer

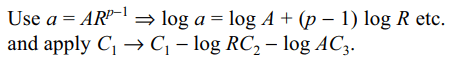
14. If pth, qth and rth terms of an H.P. be a, b, c respectively, then \[ \triangle=\begin{bmatrix}bc & ca & ab \\p & q & r \\1 & 1 & 1\end{bmatrix}\]
is
a) -1
b) abcpqr
c) pa + qb + rc
d) 0

View Answer

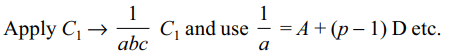
15. If \[ \triangle=\begin{bmatrix}b^{2}-ab & b-c & bc-ac \\ab-a^{2} & a-b & b^{2}-ab \\bc-ac & c-a & ab-a^{2}\end{bmatrix}\]
then \[ \triangle\] equals
a) (b – c) (c – a) (a – b)
b) abc (b – c) (c – a) (a – b)
c) (a+b+c) (b – c) (c – a) (a – b)
d) 0

View Answer

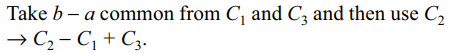
16. Let p, q, r be three distinct prime numbers, and
\[\begin{bmatrix}-pi & -qi & 1 \\r^{3} & qi & -1 \\pqr & 2q & 2i\end{bmatrix}\]     = x + iy, then
a) x = –p, y = q
b) x = r, y = 0
c) x = 0, y = –qr
d) x = 0, y = 0

View Answer

17. If a, b, c are three integers in A.P., lying between 1 and 9 and a31, b41 and c51 are three digit numbers, then the determinant \[\begin{bmatrix}3 & 4 &5 \\a31 & b41 & c51 \\a & b & c\end{bmatrix}\]     equals
a) a + b + c
b) 3b
c) -1
d) 0

View Answer

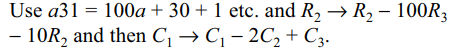
18. If \[\begin{bmatrix}1 & 1 &1 \\^{m}C_{1} & ^{m+3}C_{1} &^{m+6}C_{1} \\^{m}C_{2} & ^{m+3}C_{2} & ^{m+6}C_{2}\end{bmatrix}=2^{\alpha}3^{\beta}5^{\gamma}\]
then \[\alpha+\beta+\gamma\]   is equals to
a) 3
b) 5m
c) 7
d) \[m^{2}\]

View Answer

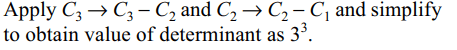
19. Let a, b, c be three non-zero complex numbers, and let \[z=\begin{bmatrix}0 & -b & -c \\b & 0 & -a \\c & a & 0\end{bmatrix}\]
then z equals
a) 0
b) purely imaginary
c) abc
d) 2abc

View Answer

20. If A, B and C are the angles of a triangle, then the determinant
\[z=\begin{bmatrix}-1 & \cos C & \cos B\\\cos C & -1 & \cos A \\\cos B & \cos A & -1\end{bmatrix}\]
is equals
a) 0
b) -1
c) 1
d) 2

View Answer

21. If \[f\left(x\right)=\begin{bmatrix}\sin 2x\left(1+2\cos x\right) &\sin2x & \sin3x\\3+4\sin x & 3 & 4\sin x \\1+\sin x & \sin x & 1\end{bmatrix}\]
then the value of \[\int_{0}^{\pi/2} f\left(x\right) d(x)\]    is
a) 3
b) 2/3
c) 1/3
d) 0

View Answer

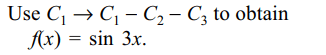
22. If \[\alpha,\beta,\gamma\]   are the roots of \[x^{3}+ax^{2}+b=0\]     , then the determinant \[\triangle\]  , where
\[\triangle=\begin{bmatrix}\alpha & \beta & \gamma \\\beta & \gamma & \alpha \\\gamma & \alpha & \beta\end{bmatrix}\]
equals
a) \[-a^{3}\]
b) \[a^{3}-3b\]
c) \[a^{2}-3b\]
d) a³

View Answer

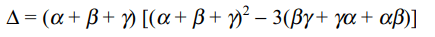
23. The number of distinct real roots of \[\triangle=\begin{bmatrix}\tan x & \cot x & \cot x \\\cot x & \tan x & \cot x \\\cot x & \cot x & \tan x\end{bmatrix}=0\]
in the interval\[-\pi/4\leq x \leq\pi/4\]     is
a) 0
b) 2
c) 1
d) 3

View Answer

24. If \[\omega \neq 1\]   is a complex cube root of unity ,and \[x+iy =\begin{bmatrix}1 & i & -\omega \\-i & 1 & \omega^{2} \\\omega & -\omega^{2} & 1\end{bmatrix}\]
then
a) x = – 1, y = 0
b) x = 1, y = – 1
c) x = 1, y = 1
d) x = 0, y = 0

View Answer

25. If \[e^{ix}=\cos x+i \sin x\]     and \[x+iy=\begin{bmatrix}1 & e^{\pi i/4} & e^{\pi i/3} \\e^{-\pi i/4} & 1 & e^{2\pi i/3} \\e^{-\pi i/3} & e^{-2\pi i/3} & e^{2\pi i}\end{bmatrix}\]
then
a) \[x = – 1, y =\sqrt{2}\]
b) \[x = 1, y =-\sqrt{2}\]
c) \[x = – \sqrt{2}, y =\sqrt{2}\]
d) none of these

View Answer

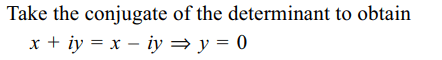
26. If a, b, \[c\epsilon R\] , the number of real roots of the equation \[\triangle=\begin{bmatrix}x & c & -b \\-c & x & a \\b & -a & x\end{bmatrix} = 0\]
is
a) 0
b) 1
c) 2
d) 3

View Answer

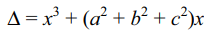
27. If a, b, \[c\epsilon R\] and a²+b²-ab-a-b+1 \[\leq\] 0 and \[\alpha+\beta+\gamma=0\]    , then \[\triangle=\begin{bmatrix}1 & \cos\gamma & \cos\beta \\\cos\gamma & a & \cos\alpha \\\cos\alpha & \cos\beta & b\end{bmatrix}\]
equals
a) ab
b) 1
c) 2
d) 3

View Answer

28. If \[\triangle=\begin{bmatrix}\sin\alpha &\cos \alpha&\sin\alpha+\cos\beta \\\sin\beta& \cos \alpha & \sin\beta+\cos\beta \\\sin\gamma & \cos \alpha & \sin\gamma+\cos\beta\end{bmatrix}\]
then \[\triangle\] is equal to
a) \[\sin\alpha\sin\beta\sin\gamma\]
b) \[\cos\alpha\sec\beta\tan\gamma\]
c) \[\sin\alpha\sin\left(\alpha+\beta\right)+\cos\alpha\cos\left(\gamma+\beta\right)\]
d) 0

View Answer

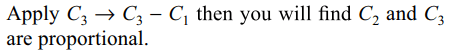
29. Let \[f\left(x\right)=\begin{bmatrix}cosec x & \sin x & cosec^2 x+\tan x \sec x \\\sin^{2}x & \sin^{2}x & \sec^{2}x \\1 & \sin^{2}x & \sin^{2}x\end{bmatrix}\]
then \[\int_{0}^{\pi/2} f\left(x\right) dx\]    equals
a) \[-\left(\frac{\pi}{4}+\frac{8}{15}\right)\]
b) \[\frac{\pi}{4}\]
c) \[\frac{\pi}{4}+\frac{1}{5}\]
d) \[\pi\]

View Answer

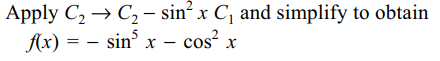
30. The values of \[\theta\]  lying between \[\theta=0\]  and \[\theta=\pi/2\]   and satisfying the equation \[\begin{bmatrix}1+\sin^{2}\theta & \cos^{2}\theta & 4\sin6\theta \\\sin^{2}\theta & 1+\cos^{2}\theta &4\sin6\theta \\\sin^{2}\theta & \cos^{2}\theta &1+ 4\sin6\theta\end{bmatrix}=0\]
are given by
a) \[\pi/36, 5\pi/36\]
b) \[7\pi/36, 11\pi/36\]
c) \[5\pi/36, 7\pi/36\]
d) \[11\pi/36, \pi/36\]

View Answer

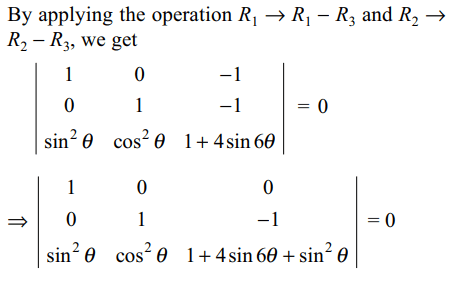
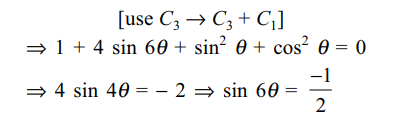
31. If \[pqr\neq0\]  and the system of equations
(p + a)x + by + cz = 0
ax + (q + b)y + cz = 0
ax + by + (r + c)z = 0
has a non-trivial solution, then value of \[\frac{a}{p}+\frac{b}{q}+\frac{c}{r}\]     is
a) -1
b) 0
c) 1
d) 2

View Answer

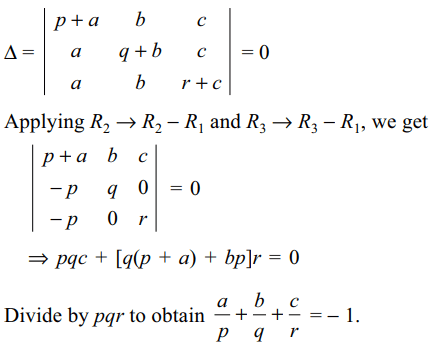
32. Let \[a = 2^{A}, b = 2^{B}, C = 2^{C}\]     the system of equations
ax + by + (a \[\alpha\] + b)z = 0
bx + cy + (b \[\alpha\] + c)z = 0
(a \[\alpha\] + b)x + (b \[\alpha\] + c)y = 0
has a non-zero solutions if A, B, C are in
a) A.P
b) G.P
c) H.P
d) none of these

View Answer

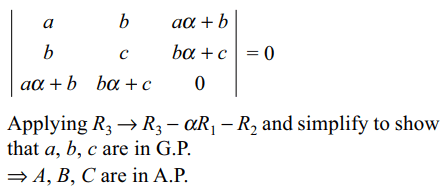
33. If the system of equations
ax + ay – z = 0
bx – y + bz = 0
– x + cy + cz = 0
(where \[a, b, c \neq – 1\]   ) has a non-trivial solution, then value of \[\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\]     is
a) 2
b) -1
c) -2
d) 0

View Answer

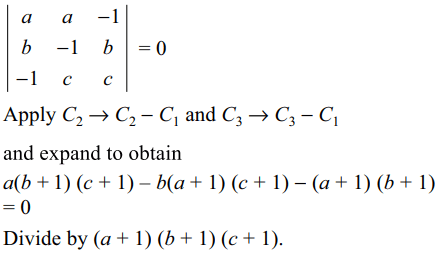
34. All the values of \[\lambda\] for which the system of equations
\[\left(\lambda + 5\right)x + \left(\lambda – 4\right)y + z = 0\]
\[\left(\lambda - 2\right)x + \left(\lambda + 3\right)y + z = 0\]
\[\lambda x+\lambda y+z=0\]
has a non-trivial solution lie in the set
a) {– 1, 2}
b) {0, – 1}
c) {0}
d) R

View Answer

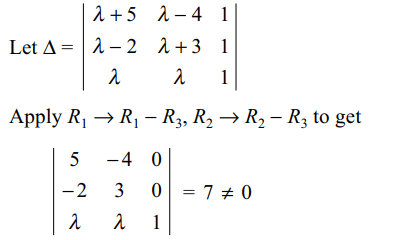
35. Given the system of equations
(b + c) (y + z) – ax = b – c
(c + a) (z + x) – by = c – a
(a + b) (x + y) – cz = a – b
(where \[a + b + c \neq 0\]   ); then x : y : z is given by
a) b – c : c – a : a – b
b) b + c : c + a : a + b
c) a : b : c
d) \[\frac{a}{b}:\frac{b}{c}:\frac{c}{a}\]

View Answer

36. Number of real values of \[\lambda\] for which the system of equations
\[\left(\lambda + 3\right)x + \left(\lambda + 2\right)y + z = 0\]
\[3x + \left(\lambda + 3\right)y + z = 0\]
2x + 3y + z = 0
has a non-trivial solutions is
a) 0
b) 1
c) 2
d) Infinite

View Answer

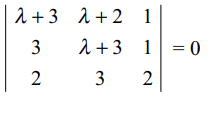
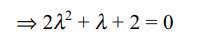
37. The value of \[\lambda\] for which the system of equations
2x – y – 2z = 2
x – 2y + z = – 4
\[x+y+\lambda z=4\]
has no solution is
a) 3
b) -3
c) 2
d) -2

View Answer

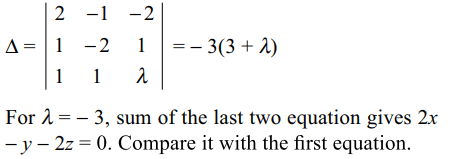
38. The determinant \[\begin{bmatrix}\sin\alpha & \cos\alpha & 1 \\\sin\beta & \cos\beta & 1 \\\sin\gamma & \cos\gamma & 1\end{bmatrix}\]         is equals to
a) \[-4\sin\frac{\alpha-\beta}{2}\sin\frac{\beta-\gamma}{2}\sin\frac{\gamma-\alpha}{2}\]
b) \[\sin\alpha+\sin\beta+\sin\gamma\]
c) \[\sin\left(\alpha-\beta\right)+\sin\left(\beta-\gamma\right)+\sin\left(\gamma-\alpha\right)\]
d) Both a and c

View Answer

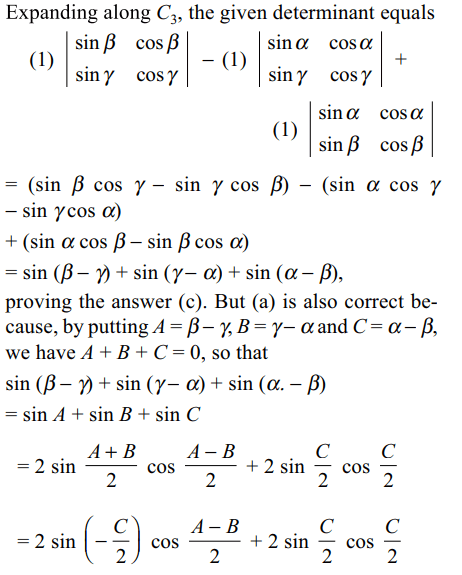
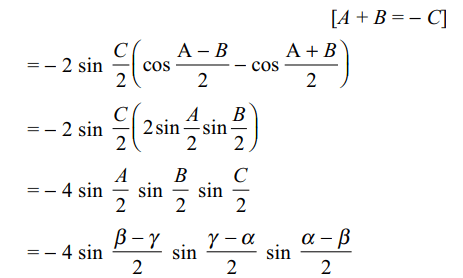
39. If a, b, c > 0 and x, y, \[z\epsilon R\] , then the determinant \[\begin{bmatrix}\left(a^{x}+a^{-x}\right)^{2} & \left(a^{x}-a^{-x}\right)^{2} & 1 \\\left(b^{y}+b^{-y}\right)^{2} & \left(b^{y}-b^{-y}\right)^{2} & 1 \\\left(c^{z}+c^{-z}\right)^{2} & \left(c^{z}-c^{-z}\right)^{2} & 1\end{bmatrix}\]
is indepenent of
a) a, b, c
b) x, y, z
c) a, b, c, x, y, z
d) All of the above

View Answer

40. If \[a\neq b\]  , the equation \[\begin{bmatrix}x & a & a \\a & x & a \\a & a & x\end{bmatrix}+\begin{bmatrix}b & b & x \\b & x & b \\x & b & b\end{bmatrix}=0\]
is satisfied when x equals
a) 0
b) a-b
c) a+b
d) \[\frac{2}{3}\frac{a^{2}+ab+b^{2}}{a+b}\]

View Answer

41. If \[a_{i}, b_{i}, c_{i} \epsilon R\]     (i = 1, 2, 3) and \[x\epsilon R\] and
\[\triangle=\begin{bmatrix}a_{1}+b_{1}x^{2}& a_{1}x^{2}+b_{1} & c_{1} \\a_{2}+b_{2}x^{2} & a_{2}x^{2}+b_{2} & c_{2} \\a_{3}+b_{3}x^{2} & a_{3}x^{2}+b_{3} & c_{3}\end{bmatrix}=0\]
then
a) x=1
b) x=-1
c) \[\begin{bmatrix}a_{1}& b_{1} & c_{1} \\a_{2}& b_{2} & c_{2} \\a_{3} &b_{3} & c_{3}\end{bmatrix}=0\]
d) All of the above

View Answer

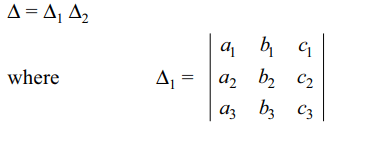
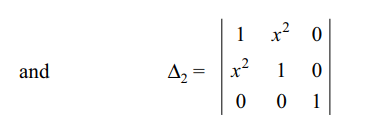
42. The determinant \[\begin{bmatrix}\sin^{2}\alpha&\sin\alpha\cos\alpha & \cos^{2} \alpha\\\sin^{2}\beta& \sin\beta\cos\beta & \cos^{2} \beta \\\sin^{2}\gamma &\sin\gamma\cos\gamma & \cos^{2} \gamma\end{bmatrix}\]
is
a) \[-\sin\left(\beta-\gamma\right)\sin\left(\gamma-\alpha\right)\sin\left(\alpha-\beta\right)\]
b) \[\sin\left(\alpha-\beta\right)\cos\alpha\cos\beta+\sin\left(\beta-\gamma\right)\cos\beta\cos\gamma+\sin\left(\gamma-\alpha\right)\cos\gamma\cos\alpha\]
c) \[\frac{1}{4}\left[sin\left(2\alpha-2\beta\right)+\sin\left(2\beta-2\gamma\right)+\sin\left(2\gamma-2\alpha\right)\right]\]
d) All of the above

View Answer

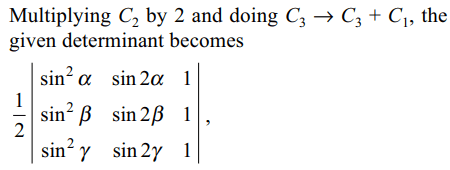
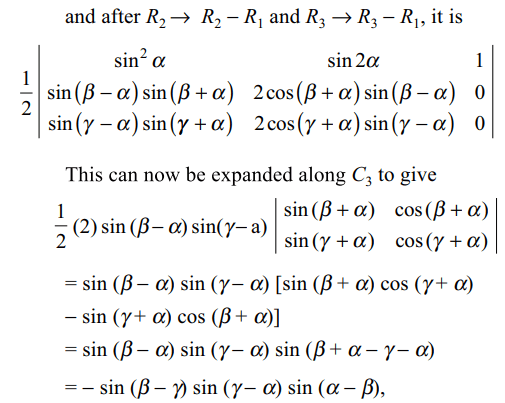
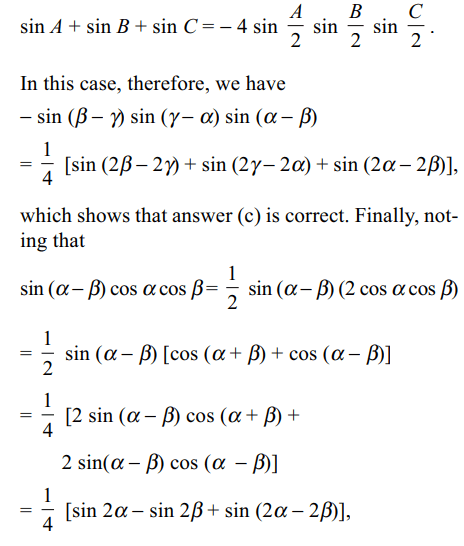
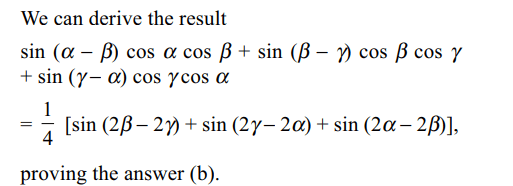
43. If \[a^{2}+b^{2}+c^{2}=1\]   , then
\[\begin{bmatrix}a^{2}+\left(b^{2}+c^{2}\right)\cos\phi & ab \left(1-\cos\phi\right) & ac \left(1-\cos\phi\right) \\ba \left(1-\cos\phi\right) & b^{2}+\left(c^{2}+a^{2}\right)\cos\phi & bc \left(1-\cos\phi\right) \\ca \left(1-\cos\phi\right) & cb \left(1-\cos\phi\right) & c^{2}+\left(a^{2}+b^{2}\right)\cos\phi \end{bmatrix}\]
is independent of
a) a
b) b
c) c
d) All of the above

View Answer

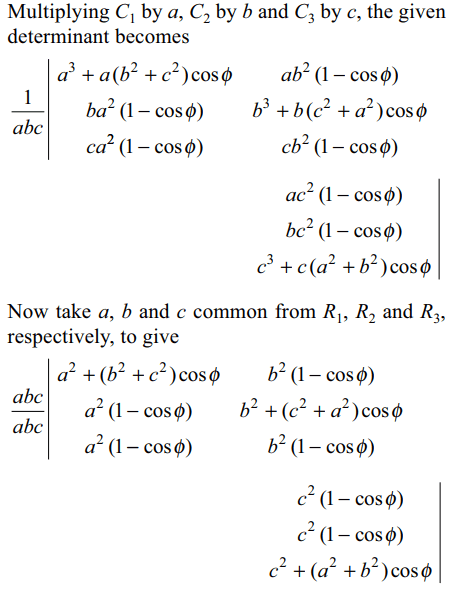
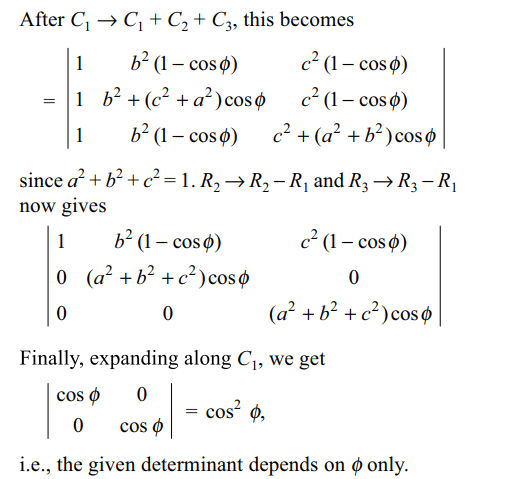
44. If \[\triangle=\begin{bmatrix}\sin\alpha & \cos\alpha & \sin\left(\alpha+\delta\right) \\\sin\beta & \cos\beta & \sin\left(\beta+\delta\right) \\\sin\gamma & \cos\gamma & \sin\left(\gamma+\delta\right) \end{bmatrix}\]
then \[\triangle\] is independent of
a) \[\alpha\]
b) \[\beta\]
c) \[\gamma\]
d) All of the above

View Answer

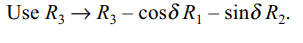
45. If \[\phi\epsilon R\]  then
\[\triangle\left(\phi\right)=\begin{bmatrix}\sin \phi & \cos \phi & \sin 2\phi \\\sin\left(\phi +2\pi/3\right) & \cos\left(\phi +2\pi/3\right) & \sin\left(2\phi +4\pi/3\right) \\\sin\left(\phi -2\pi/3\right) & \cos\left(\phi -2\pi/3\right) & \sin\left(2\phi -4\pi/3\right)\end{bmatrix}\]
a) is independent of \[\phi\]
b) is equal to a constant
c) has no local maximum
d) All of the above

View Answer

46. If \[abc\neq0\]  , then
\[\triangle\left(x\right)=\begin{bmatrix}a^{2}\left(1+x\right) & ab & ac \\ab & b^{2}\left(1+x\right) & bc \\ac & bc & c^{2}\left(1+x\right)\end{bmatrix}\]
is divisible by
a) \[3+x\]
b) x
c) \[x^{2}\]
d) All of the above

View Answer

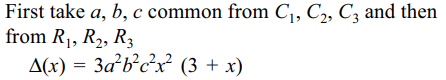
47. If a, b and c are the sides of a triangle and A, B and C are the angles opposite to a, b and c respectively, then \[\triangle=\begin{bmatrix}a^{2} & b\sin A & c\sin A \\b\sin A & 1 & \cos A \\c\sin A & \cos A & 1\end{bmatrix}\]
is independent of
a) a
b) b
c) c
d) All of the above

View Answer

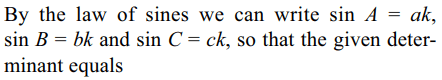
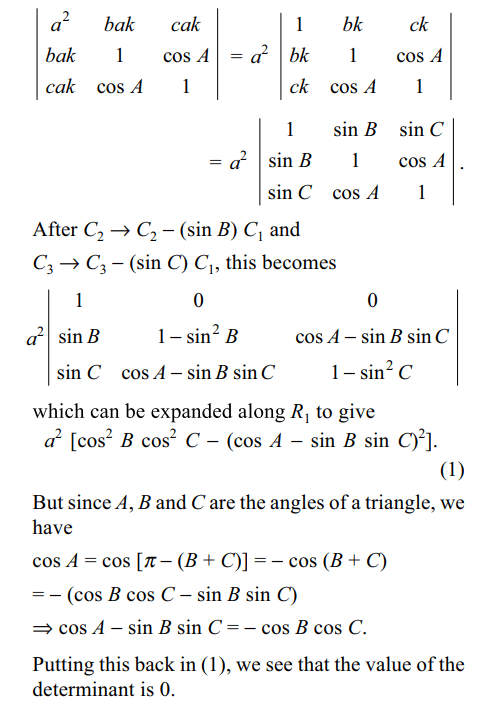
48. If A, B and C are the angles of a triangle and
\[\triangle\left(x\right)=\begin{bmatrix}1 & 1 & 1 \\1+\sin A & 1+\sin B & 1+\sin C \\\sin A+\sin^{2}A & \sin B+\sin^{2}B & \sin C+\sin^{2}C\end{bmatrix}=0\]
then the triangle must be
a) isosceles
b) equilateral
c) right angled
d) none of these

View Answer

49. If a_i, b_i ∈ N for i = 1,2,3 then the coefficient of x in the determinant
\[\begin{bmatrix}\left(1+x\right)^{a_{1}b_{1}} & \left(1+x\right)^{a_{1}b_{2}} & \left(1+x\right)^{a_{1}b_{3}} \\\left(1+x\right)^{a_{2}b_{1}} & \left(1+x\right)^{a_{2}b_{2}} & \left(1+x\right)^{a_{2}b_{3}} \\\left(1+x\right)^{a_{3}b_{1}} & \left(1+x\right)^{a_{3}b_{2}} & \left(1+x\right)^{a_{3}b_{3}}\end{bmatrix}\]
a) 0
b) \[a_{1}+a_{2}+a_{3}\]
c) independent of \[a_{i},s+b_{i},s\]
d) Both a and c

View Answer

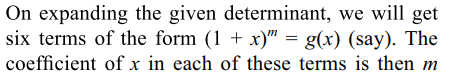
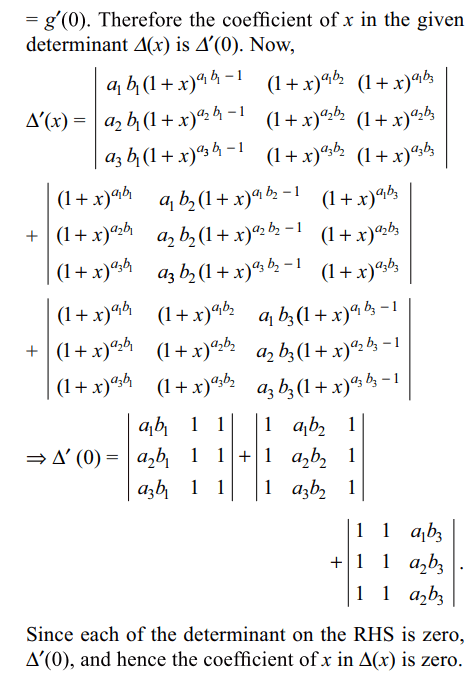
50. Let \[f\left(x\right)=\begin{bmatrix}\cos x & \sin x & \cos x \\\cos 2x & \sin 2x & 2\cos 2x \\\cos 3x & \sin 3x & 3\cos 3x \end{bmatrix}\]
then
a) f '(0) = 0
b) \[f'\left(\pi/2\right)=4\]
c) \[f'\left(\pi\right)=0\]
d) All of the above

View Answer