PrepBharat

1. If a, b, c are non-zero real numbers, then \[\triangle=\begin{bmatrix}1 & ab &\frac{1}{a}+\frac{1}{b} \\1 & bc & \frac{1}{b}+\frac{1}{c} \\1 & ca & \frac{1}{c}+\frac{1}{a}\end{bmatrix}\]
is
a) 0
b) bc + ca + ab
c) \[a^{-1}+b^{-1}+c^{-1}\]
d) none of these

View Answer

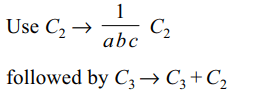
2. If a, b, c > 1 , \[\triangle=\begin{bmatrix}\log_{a}\left(abc\right) & \log_{a}b &\log_{a}c \\\log_{b}\left(abc\right) & 1 & \log_{b}c \\\log_{c}\left(abc\right) & \log_{c}b & 1\end{bmatrix}\]
is
a) 0
b) \[ \log_{a}b+ \log_{b}c+ \log_{c}a\]
c) \[ \log_{abc}\left(a+b+c\right)\]
d) 3

View Answer

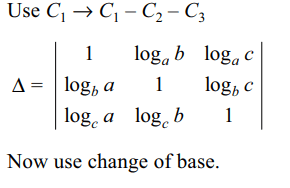
3. If a, b, c are positive and are the pth, qth and rth terms respectively of a G.P., then \[ \triangle=\begin{bmatrix}\log a & p & 1 \\\log b & q & 1 \\\log c & r & 1\end{bmatrix}\]
is
a) 0
b) log (abc)
c) – (p + q + r)
d) 3

View Answer

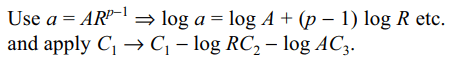
4. If pth, qth and rth terms of an H.P. be a, b, c respectively, then \[ \triangle=\begin{bmatrix}bc & ca & ab \\p & q & r \\1 & 1 & 1\end{bmatrix}\]
is
a) -1
b) abcpqr
c) pa + qb + rc
d) 0

View Answer

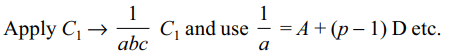
5. If \[ \triangle=\begin{bmatrix}b^{2}-ab & b-c & bc-ac \\ab-a^{2} & a-b & b^{2}-ab \\bc-ac & c-a & ab-a^{2}\end{bmatrix}\]
then \[ \triangle\] equals
a) (b – c) (c – a) (a – b)
b) abc (b – c) (c – a) (a – b)
c) (a+b+c) (b – c) (c – a) (a – b)
d) 0

View Answer

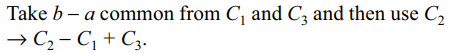
6. Let p, q, r be three distinct prime numbers, and
\[\begin{bmatrix}-pi & -qi & 1 \\r^{3} & qi & -1 \\pqr & 2q & 2i\end{bmatrix}\]     = x + iy, then
a) x = –p, y = q
b) x = r, y = 0
c) x = 0, y = –qr
d) x = 0, y = 0

View Answer

7. If a, b, c are three integers in A.P., lying between 1 and 9 and a31, b41 and c51 are three digit numbers, then the determinant \[\begin{bmatrix}3 & 4 &5 \\a31 & b41 & c51 \\a & b & c\end{bmatrix}\]     equals
a) a + b + c
b) 3b
c) -1
d) 0

View Answer

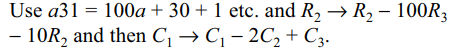
8. If \[\begin{bmatrix}1 & 1 &1 \\^{m}C_{1} & ^{m+3}C_{1} &^{m+6}C_{1} \\^{m}C_{2} & ^{m+3}C_{2} & ^{m+6}C_{2}\end{bmatrix}=2^{\alpha}3^{\beta}5^{\gamma}\]
then \[\alpha+\beta+\gamma\]   is equals to
a) 3
b) 5m
c) 7
d) \[m^{2}\]

View Answer

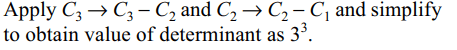
9. Let a, b, c be three non-zero complex numbers, and let \[z=\begin{bmatrix}0 & -b & -c \\b & 0 & -a \\c & a & 0\end{bmatrix}\]
then z equals
a) 0
b) purely imaginary
c) abc
d) 2abc

View Answer

10. If A, B and C are the angles of a triangle, then the determinant
\[z=\begin{bmatrix}-1 & \cos C & \cos B\\\cos C & -1 & \cos A \\\cos B & \cos A & -1\end{bmatrix}\]
is equals
a) 0
b) -1
c) 1
d) 2

View Answer