PrepBharat

1.If \[D_{1}\] and \[D_{2}\] are two \[3 \times3\]  diagonal matrices, then
a) \[D_{1}D_{2}\]  is diagonal matrix
b) \[D_{1}D_{2}=D_{2}D_{1}\]
c) \[D_1^2+D_2^2\]  is a diagonal matrix
d) All of the above

View Answer

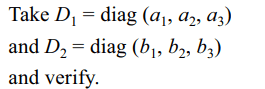
2. Let \[A=\begin{bmatrix}1 & 0 \\1 & 1 \end{bmatrix}\]   then
a) \[A^{-n}=\begin{bmatrix}1 & 0 \\-n & 1 \end{bmatrix}\forall n \epsilon N\]
b) \[\lim_{n \rightarrow \infty}\frac{1}{n^{2}}A^{-n}=\begin{bmatrix}0 & 0 \\0 & 0 \end{bmatrix}\]
c) \[\lim_{n \rightarrow \infty}\frac{1}{n}A^{-n}=\begin{bmatrix}0 & 0 \\-1 & 0 \end{bmatrix}\]
d) All of the above

View Answer

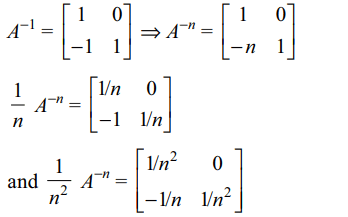
3. Let A, B and C be \[2 \times2\]  matrices with entries from the set of real numbers. Define '*' as follows
\[A*B=\frac{1}{2}\left(AB+BA\right)\]     , then
a) A * B = B * A
b) \[A * A = A^{2}\]
c) A * (B + C) = A * B + A * C
d) All of the above

View Answer

4. With A, B, C as in Q.No.3, define 'o' as follows: \[AoB=\frac{1}{2}\left(AB-BA\right)\]     , then
a) AoA = O
b) AoI = O
c) Ao(B + C) = AoB + AoC
d) All of the above

View Answer

5. Suppose a, b > 0 and let \[\triangle\left(x\right)=\begin{bmatrix}x & a & b \\a & x & b \\a & b & x\end{bmatrix},x \epsilon R\]
then \[\frac{\triangle'\left(0\right)}{\triangle\left(0\right)}\]   is equal to
a) \[\frac{1}{a+b}\]
b) \[1-\left(\frac{1}{a}+\frac{1}{b}\right)\]
c) 0
d) \[\frac{1}{a+b}-\frac{1}{a}-\frac{1}{b}\]

View Answer

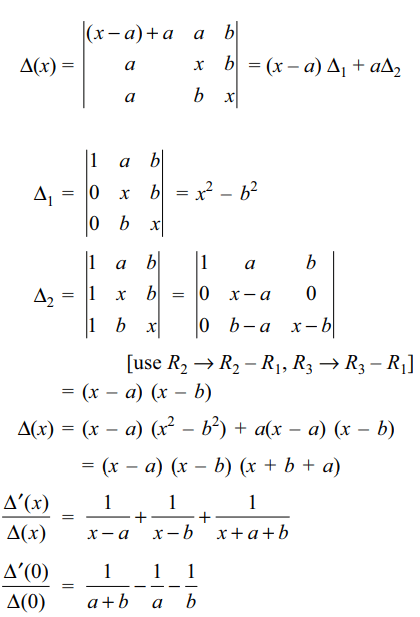
6. Let \[\triangle=\begin{bmatrix}ln \left(2/15\right) & ln\left(4\right) & ln\left(4\right) \\ ln\left(9\right) & ln\left(3/10\right) & ln\left(9\right) \\ ln\left(25\right) & ln\left(25\right) & ln\left(5/6\right)\end{bmatrix}\]
then \[\triangle\] is equal to
a) \[\left[ln\left(30\right)\right]^{3}\]
b) \[\left[ln\left(60\right)\right]^{3}\]
c) \[\left[ln\left(30\right)\right]^{2}\]
d) \[\left[ln\left(60\right)\right]^{2}\]

View Answer

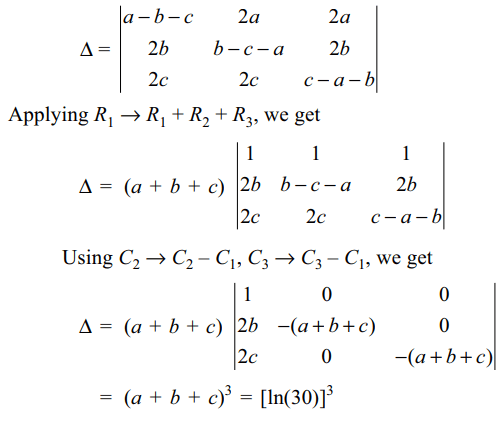
7. Let \[\triangle\] ABC be an acute angled triangle such that
\[\frac{\tan A}{\tan B}-\frac{\tan B}{\tan A}+\frac{\tan B}{\tan C}-\frac{\tan C}{\tan B}+\frac{\tan C}{\tan A}-\frac{\tan A}{\tan C}=0\]
then
a) \[\triangle ABC\]   is an equilateral triangle
b) \[\triangle ABC\]   is an isosceles triangle
c) one of the angles of \[\triangle ABC\]   is \[\pi/3\]
d) one of the angle of \[\triangle ABC\]   must be \[\pi/4\]

View Answer

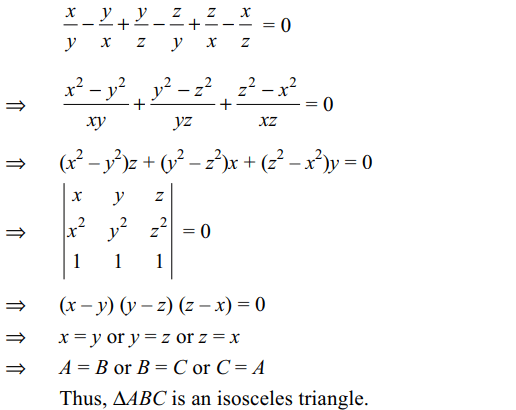
8. Let a, b, c be distinct positive real numbers such that \[S=\sum\frac{1}{a\left(a-b\right)\left(a-c\right)}\]     and \[T=\frac{1}{abc}\]
then
a) S=T
b) S+T=0
c) S = (a + b + c)T
d) S = (bc + ca + ab)T

View Answer

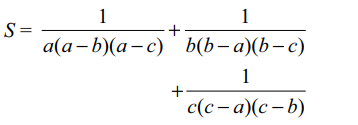
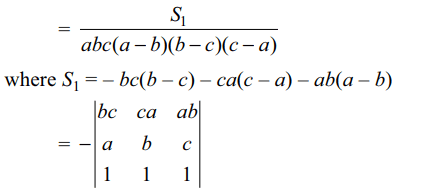
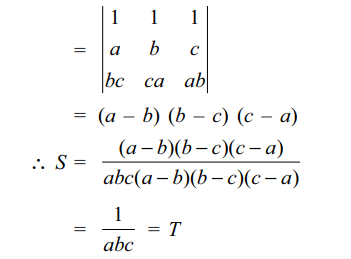
9. Let x, y, z be three real distinct real numbers, and let
\[S=\begin{bmatrix}x+y^{2} & y+z^{2} & z+x^{2} \\x^{2}+y^{3} & y^{2}+z^{3} & z^{2}+x^{3} \\x^{3}+y^{4} & y^{3}+z^{4} & z^{3}+x^{4}\end{bmatrix}\]
and \[T=\begin{bmatrix}1 & 1 & 1 \\x & y & z \\x^{2} & y^{2} & z^{2}\end{bmatrix}\]
then
a) \[\frac{\triangle}{\triangle_{1}}=xyz \]
b) \[\frac{\triangle_{1}}{\triangle}=\frac{1}{1+x^{2}y^{2}z^{2}}\]
c) \[\frac{\triangle_{1}}{\triangle}=\frac{1}{1+xyz}\]
d) \[\frac{\triangle_{1}}{\triangle}=xyz +x^{2}y^{2}z^{2}\]

View Answer

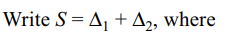
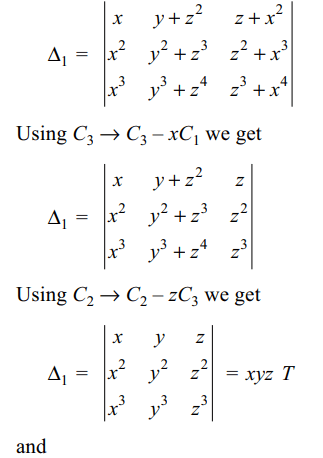
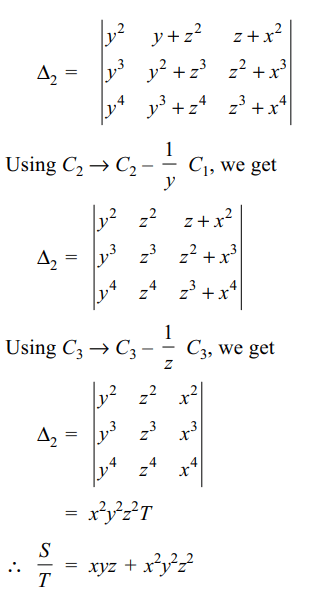
10. Let \[A=\left(a_{ij}\right)_{3\times 3}\]     be such that det(A) = 5. Suppose \[b_{ij}=2^{i+j}a_{ij}\left(1\leq i, j\leq3\right)\]       and let \[B=\left(b_{ij}\right)_{3 \times 3}\]     , then det(B) is equal to
a) \[2^{16}\]
b) \[2^{15}\]
c) \[2^{14}\]
d) \[2^{12}\]

View Answer

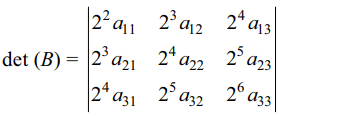
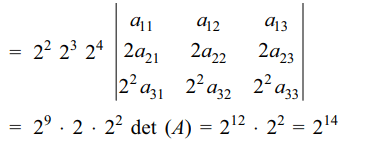
11. Let m be a positive integer, a, b, c be three real numbers and
\[\triangle_{r}=\begin{bmatrix}2r-1 & ^{m}C_{r} & 1 \\m^{2}-1 & 2^m & m+1 \\a & b & c\end{bmatrix}\]               \[(0\leq r\leq m)\]
Then the value of \[\sum_{r=0}^{m}\triangle_{r}\]   is given by
a) 0
b) \[m^{2}-1\]
c) \[2^{m}abc\]
d) \[2^{m}\left(a+b+c\right)\]

View Answer

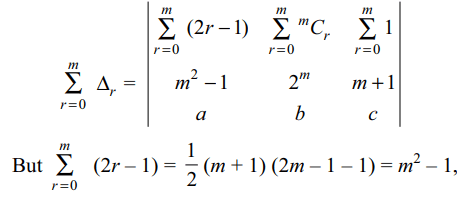
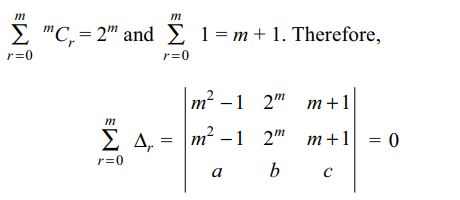
12. If \[\alpha,\beta\]  and \[\gamma\] are real numbers, then \[\triangle=\begin{bmatrix}1 & \cos\left(\beta-\alpha\right) & \cos\left(\gamma-\alpha\right) \\\cos\left(\alpha-\beta\right) & 1 & \cos\left(\gamma-\beta\right) \\\cos\left(\alpha-\gamma\right) & \cos\left(\beta-\gamma\right) & 1\end{bmatrix}\]
is equal to
a) -1
b) \[\cos\alpha\cos\beta\cos\gamma\]
c) \[\cos\alpha+\cos\beta+\cos\gamma\]
d) 0

View Answer

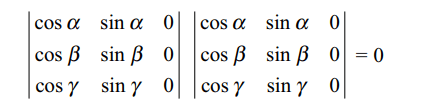
13. If a + b + c > 0, and \[\triangle=\begin{bmatrix}a & b & c \\b & c & a \\c & a & b\end{bmatrix}\]     , then
a) \[\triangle< 0\]
b) \[\triangle\leq 0\]
c) \[\triangle> 0\]
d) \[\triangle= 0\]

View Answer

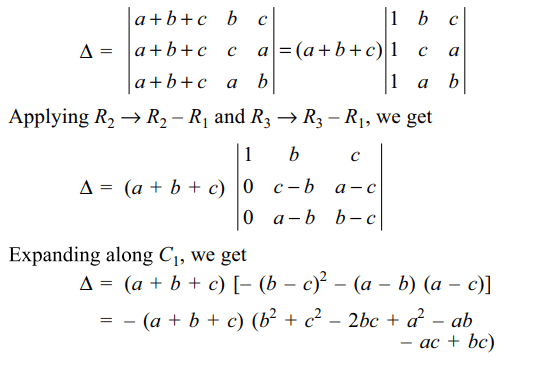
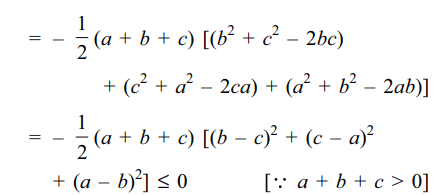
14. If \[p\lambda^{4}+q\lambda^{3}+r\lambda^{2}+s\lambda+t=\begin{bmatrix}\lambda^{2}+3\lambda & \lambda-1 & \lambda+3 \\\lambda^{2}+1 & 2+5\lambda & \lambda-3 \\\lambda^{2}-3 & \lambda+4 & 3\lambda\end{bmatrix}\]
then p is equal to
a) 5
b) 8
c) 3
d) 2

View Answer

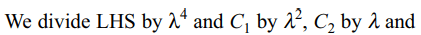
15. If \[\begin{bmatrix}x-1 & 5x & 7 \\x^{2}-1 & x-1 & 8 \\2x &3x & 0\end{bmatrix}=ax^{3}+bx^{2}+cx+d\]
then value of c is given by
a) -1
b) 12
c) 15
d) 17

View Answer

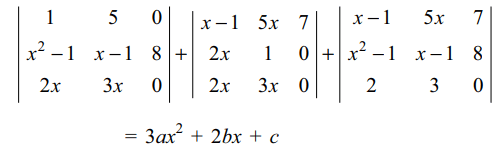
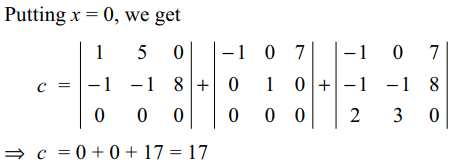
16. If \[l_1^2+m_1^2+n_1^2=1\]     , etc., and \[l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}=0\]     , etc. and \[\triangle=\begin{bmatrix}l_{1} & m_{1} & n_{1} \\l_{2} & m_{2} & n_{2} \\l_{3} &m_{3} & n_{3}\end{bmatrix}\]
then
a) \[\mid \triangle\mid=3\]
b) \[\mid \triangle\mid=2\]
c) \[\mid \triangle\mid=1\]
d) \[ \triangle=0\]

View Answer

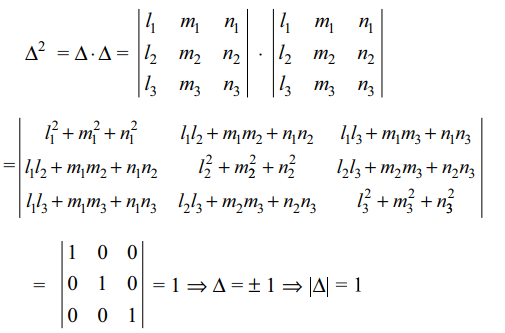
17. The complex number \[Z=\begin{bmatrix}2 & 3+i & -3 \\3-i & 0 & -1+i \\-3&-1-i & 4\end{bmatrix}\]
is equal to
a) 3-4i
b) 5+4i
c) -5i
d) -23

View Answer

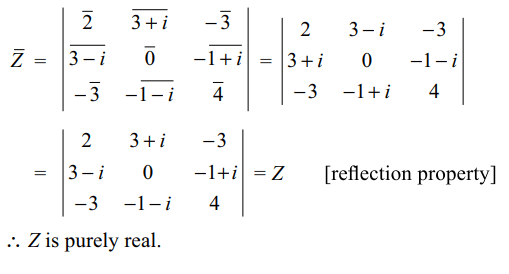
18. If \[a_{1},b_{2},c_{3} \neq 0\]
\[\triangle_{1}=\begin{bmatrix}a^2_{1}+b_{1}+c_{1} & a_{1}a_{2}+b_{2}+c_{2} & a_{1}a_{3}+b_{3}+c_{3} \\b_{1}b_{2}+c_{1} & b^2_{2}+c_{2} & b_{2}b_{3}+c_{3} \\c_{3}c_{1} & c_{3}c_{2} & c^2_{3}\end{bmatrix}\]
and \[\triangle_{2}=\begin{bmatrix}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{bmatrix}\]
, then \[\frac{\triangle_{1}}{\triangle_{2}}\]  is equal to
a) \[a_{1}b_{2}c_{3} \]
b) \[a_{1}a_{2}a_{3} \]
c) \[a_{3}b_{2}c_{1} \]
d) \[a_{1}b_{1}c_{1} +a_{2}b_{2}c_{2}+a_{3}b_{3}c_{3}\]

View Answer

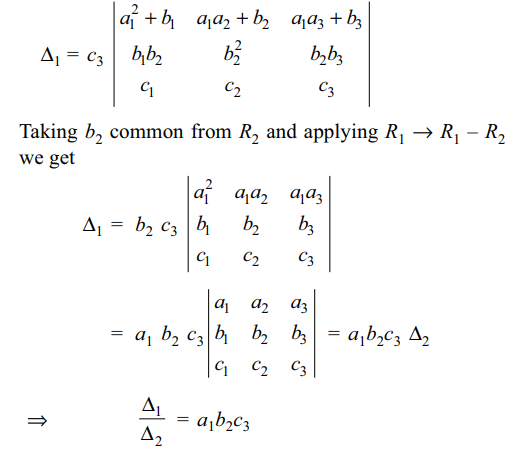
19. For a, b, c, x, y, \[z\epsilon R\] , if
\[\triangle_{1}=\begin{bmatrix}\left(a-x\right)^{2} & \left(b-x\right)^{2} & \left(c-x\right)^{2} \\\left(a-y\right)^{2} & \left(b-y\right)^{2} & \left(c-y\right)^{2} \\\left(a-z\right)^{2} & \left(b-z\right)^{2} & \left(c-z\right)^{2}\end{bmatrix}\]
and \[\triangle_{2}=\begin{bmatrix}\left(1+ax\right)^{2} & \left(1+bx\right)^{2} & \left(1+cx\right)^{2} \\\left(1+ay\right)^{2} & \left(1+by\right)^{2} & \left(1+cy\right)^{2} \\\left(1+az\right)^{2} & \left(1+bz\right)^{2} & \left(1+cz\right)^{2}\end{bmatrix}\]
then
a) \[\triangle_{1}= \triangle_{2}\]
b) \[\triangle_{1}+ \triangle_{2}=0\]
c) \[\triangle_{1}=2\triangle_{2}\]
d) \[\triangle_{1}= -2\triangle_{2}\]

View Answer

20. Let f(x) \[=\begin{bmatrix}\sec x & \cos x & \sec^{2}x+\cot x cosec x \\\cos^{2}x & \cos^{2}x & cosec^{2}x \\1 & \cos^{2}x & cosec^{2}x\end{bmatrix}\]
then value of \[\int_{0}^{\pi/2} f\left(x\right)\]   dx is
a) 0
b) \[\pi/48\]
c) \[-\frac{\pi}{2}-\frac{\pi}{15\sqrt{2}}\]
d) \[\frac{1}{3}-\frac{\pi}{4}\]

View Answer

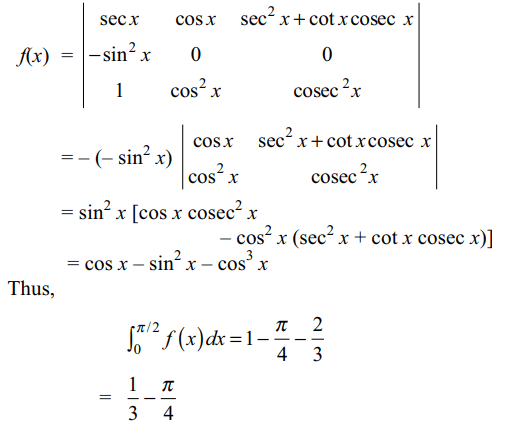
21. For a fixed positive integer n, let
\[D=\begin{bmatrix}\left(n-1\right)! & \left(n+1\right)! & \left(n+3\right)!/n\left(n+1\right)\\\left(n+1\right)! & \left(n+3\right)! & \left(n+5\right)!/\left(n+2\right)\left(n+3\right) \\\left(n+3\right)! & \left(n+5\right)! & \left(n+7\right)!/\left(n+4\right)\left(n+5\right)\end{bmatrix}\]
then \[\frac{D}{\left(n-1\right)!\left(n+1\right)!\left(n+3\right)!}\]     is equal to
a) -8
b) -16
c) -32
d) -64

View Answer

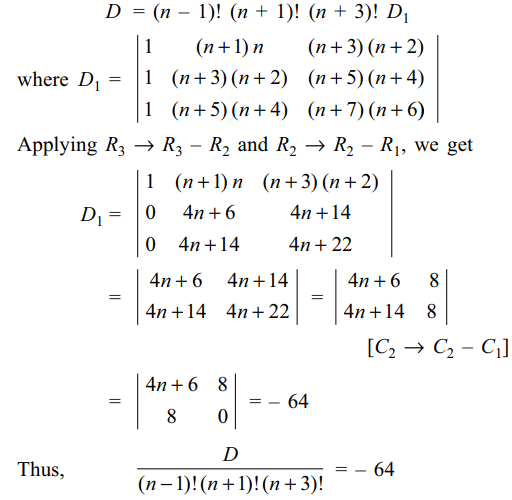
22. If \[\triangle=\begin{bmatrix}\sqrt{6} & 2i & 3+\sqrt{6} \\\sqrt{12} & \sqrt{3}+\sqrt{8}i& 3\sqrt{2}+\sqrt{6}i \\ \sqrt{18} & \sqrt{2}+\sqrt{12}i & \sqrt{27}+2i\end{bmatrix}\]
then \[\triangle\] is
a) a natural number
b) a negative integer
c) an irrational number
d) an imaginary number

View Answer

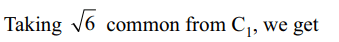
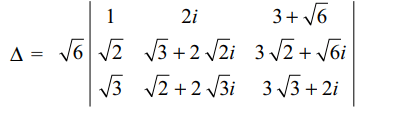
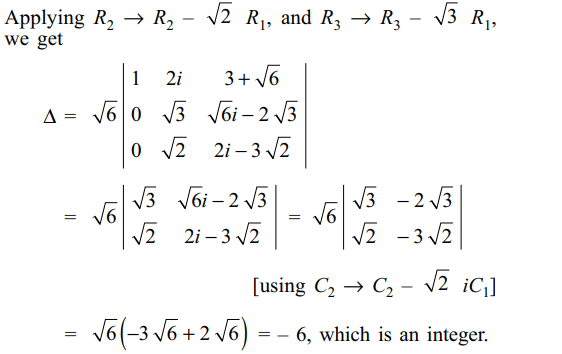
23. If x, y, z are different from zero and \[\triangle=\begin{bmatrix}a & b-y & c-z \\a-x & b & c-z \\a-x & b-y & c\end{bmatrix}=0\]
then the value of the expression \[\frac{a}{x}+\frac{b}{y}+\frac{c}{z}\]     is
a) 0
b) -1
c) 1
d) 2

View Answer

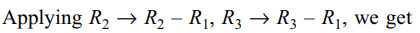
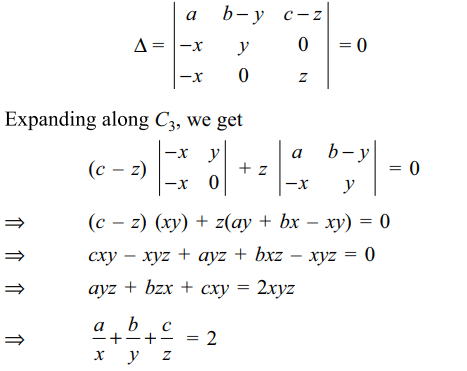
24. Let \[f\left(x\right)=\begin{bmatrix}\cos x & x & 1 \\2\sin x & x^{2} & 2x \\\tan x & x &2\end{bmatrix}\]
\[\lim_{x \rightarrow 0}\frac{f\left(x\right)}{x^{2}}\]   is equal to
a) -1
b) 0
c) 2
d) 3

View Answer

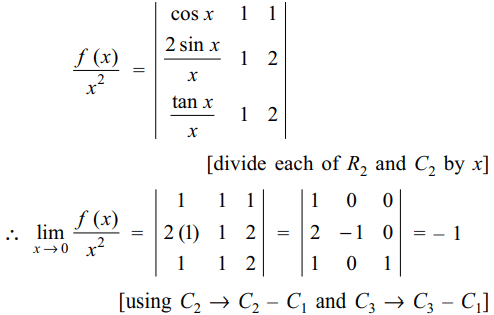
25. If \[ p \neq a, q\neq b, r\neq c\]     and the system of equations
px + ay + az = 0
bx + qy + bz = 0
cx + cy + rz = 0
has a non-trivial solution, then the value of \[\frac{p}{p-a}+\frac{q}{q-b}+\frac{r}{r-c}\]
a) -1
b) 0
c) 1
d) 2

View Answer

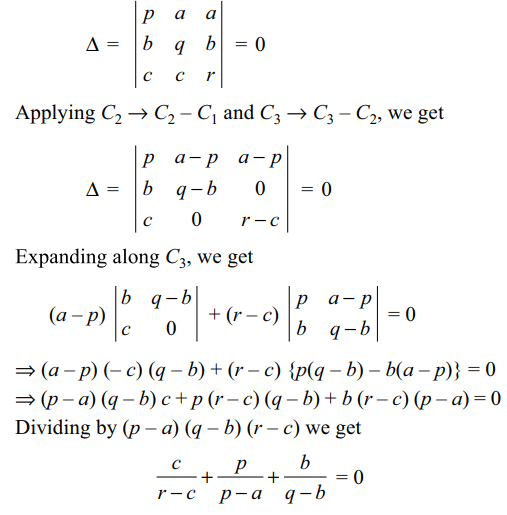
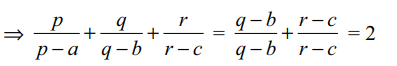
26. If \[p\neq 0\]  , solution set of the equation
\[\triangle=\begin{bmatrix}1 & 1 & x \\p+1 & p+1 & p+x \\3 & x+1 & x+2\end{bmatrix}=0\]
is
a) {1, 2}
b) {2, 3}
c) {1, p, 2}
d) {1, 2, – p}

View Answer

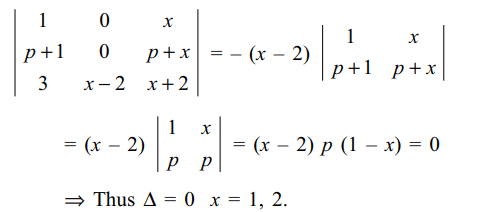
27. Let a, b, \[c\epsilon R\]   be such that \[a+b+c\neq 0\]   . If the system of equations
ax + by + cz = 0
bx + cy + az = 0
cx + ay + bz = 0
has a non-trivial solution, then
a) a + c – b = 0
b) b + c – a = 0
c) a + b – c = 0
d) a = b = c

View Answer

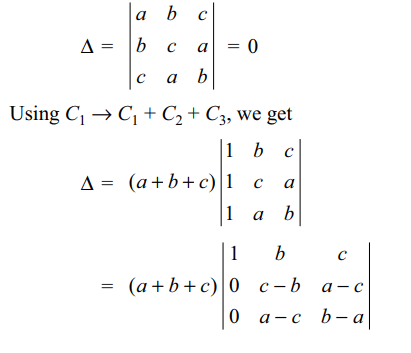
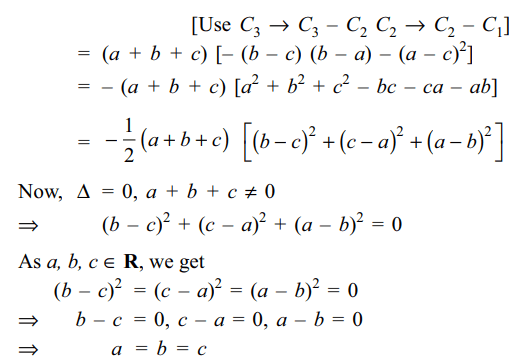
28. If the system of linear equations x + y + z = 6, x + 2y + 3z = 14 and \[2x+5y+\lambda z=\mu\left(\lambda,\mu\epsilon R\right)\]
has a unique solution, then
a) \[\lambda\neq 8\]
b) \[\lambda=8,\mu\neq 36\]
c) \[\lambda=8,\mu=36\]
d) none of these

View Answer

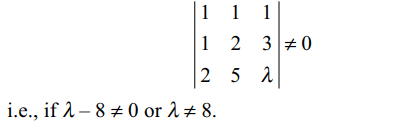
29. Let \[A\left(z_{1}\right)\]   , \[B\left(z_{2}\right)\]   and \[C\left(z_{3}\right)\]  be the vertices of a triangle. Let a = BC, b = CA and c = AB, then
\[b\begin{bmatrix}z & \bar{z} & 1 \\z_{1} & \bar{z_{1}} & 1 \\z_{2} & \bar{z_{2}} & 1\end{bmatrix}+c\begin{bmatrix}z & \bar{z} & 1 \\z_{1} & \bar{z_{1}} & 1 \\z_{3} & \bar{z_{3}} & 1\end{bmatrix}=0\]
represents
a) median of \[\triangle ABC\]   through A
b) angle bisector of \[\angle A\]
c) altitude of \[\triangle ABC\]   through A
d) perpendicular bisector of side BC

View Answer

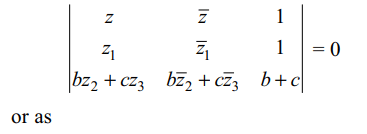
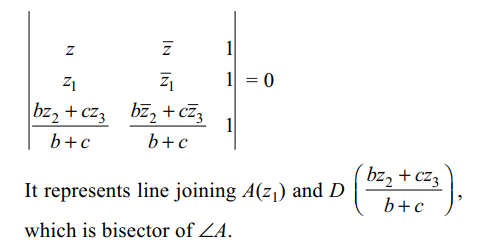
30. Suppose a, b, c are distinct real numbers and let
\[S=\begin{bmatrix}1 & a & a^{2} \\1 & b & b^{2} \\1 & c & c^{2}\end{bmatrix} S_{1}=\begin{bmatrix}1 & a & a^{3} \\1 & b & b^{3} \\1 & c & c^{3}\end{bmatrix} S_{2}=\begin{bmatrix}1 & a^{2} & a^{3} \\1 & b^{2} & b^{3} \\1 & c^{2} & c^{3}\end{bmatrix} S_{3}=\begin{bmatrix}a & a^{2} & a^{3} \\b & b^{2} & b^{3} \\c & c^{2} & c^{3}\end{bmatrix}\]
then
a) \[\frac{s_{1}}{s}=a+b+c\]
b) \[\frac{s_{2}}{s}=ab+bc+ca\]
c) \[\frac{s_{3}}{s}=abc\]
d) All of the above

View Answer

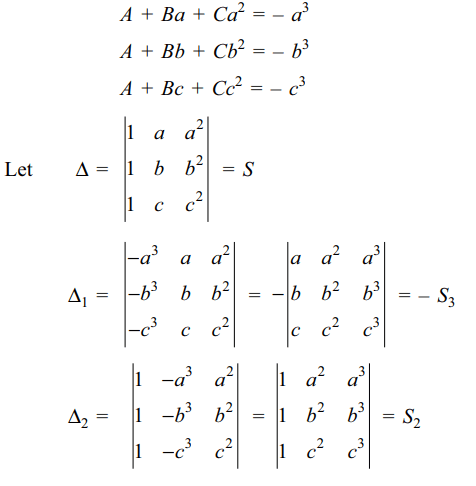
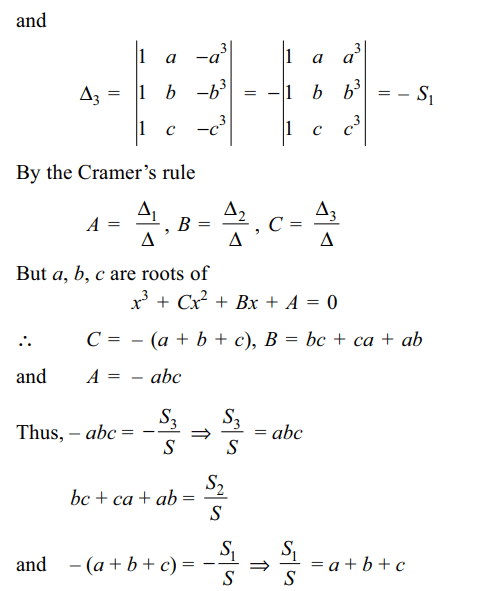
31. Suppose a, b, c, x, y, z > 0 and satisfy the system of linear equations
cy + bz = a
cx + az = b
bx + ay = c
then
a) a, b, c are sides of an acute angled triangle
b) x, y, z are cosines of the angles of an acute angled triangle
c) Each of x, y, z < 1
d) All of the above

View Answer

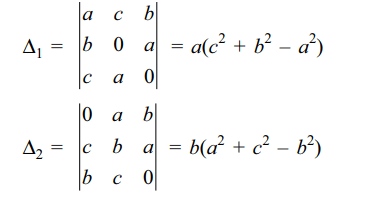
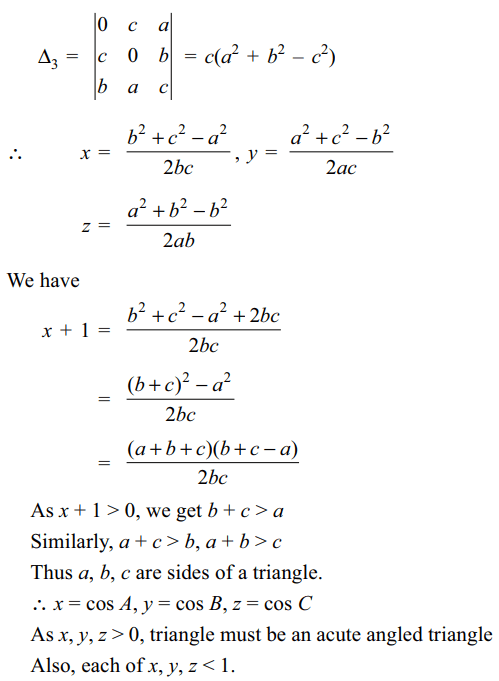
32. For \[\theta\epsilon\left[0,2\pi\right]\]   , let \[\triangle\left(\theta\right)=\begin{bmatrix}\cos\theta & \cos2\theta & \cos3\theta \\\cos2\theta & \cos3\theta & \cos4\theta \\\cos3\theta & \cos4\theta & \cos5\theta\end{bmatrix}\]
then
a) \[\triangle\left(\frac{5\pi}{12}\right)=0\]
b) \[\triangle\left(\frac{7\pi}{12}\right)=-1\]
c) \[\triangle\left(\frac{2\pi}{3}\right)=0\]
d) Both a and c

View Answer

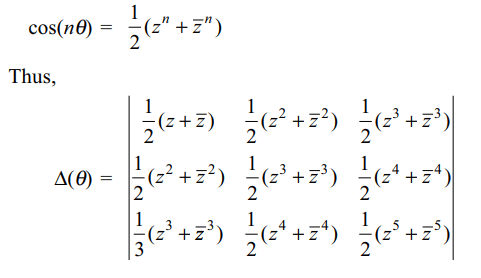
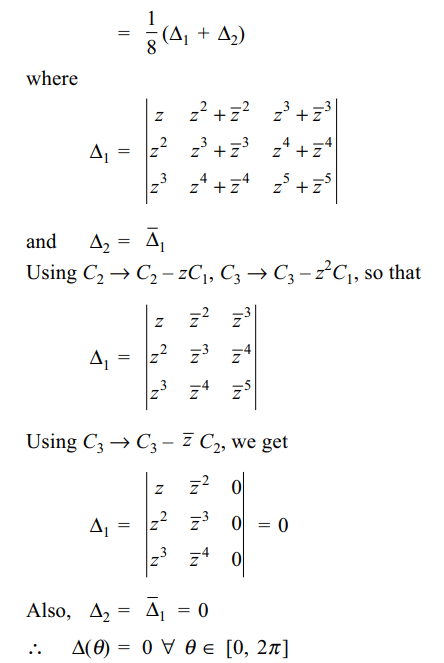
33. The determinant
\[\triangle=\begin{bmatrix}a & b & a\alpha+b \\b & c & b\alpha+c \\a\alpha+b & b\alpha+c & 0\end{bmatrix}\]
is equal to zero if
a) a, b, c are in A.P
b) a, b, c are in G.P.
c) \[\alpha\] is a root of \[ax^{2}+2bx+c=0\]
d) Both b and c

View Answer

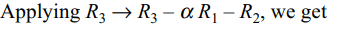
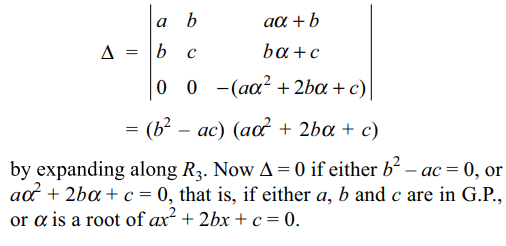
34. If \[\triangle(x)=\begin{bmatrix}x^{2}-5x+3 &2x-5 & 3 \\3x^{2}+x+4 & 6x+1 & 9 \\7x^{2}-6x+9 & 14x-6 & 21\end{bmatrix}=ax^{3}+bx^{2}+cx+d\]
then
a) a = 0
b) b = 0
c) c = 0
d) All of the above

View Answer

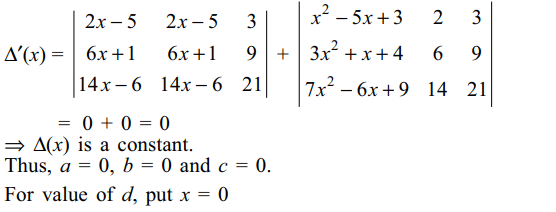
35. If \[\triangle=\begin{bmatrix}1/z & 1/z & -\left(x+y\right)/z^{2} \\-\left(y+z\right)/x^{2} & 1/x & 1/x \\-y\left(y+z\right)/x^{2}z & \left(x+2y+z\right)/xz & -\left(x+y\right)/xz^{2}\end{bmatrix}\]
then
a) \[\triangle\] is independent of x
b) \[\triangle\] is independent of y
c) \[\triangle=0\]
d) All of the above

View Answer

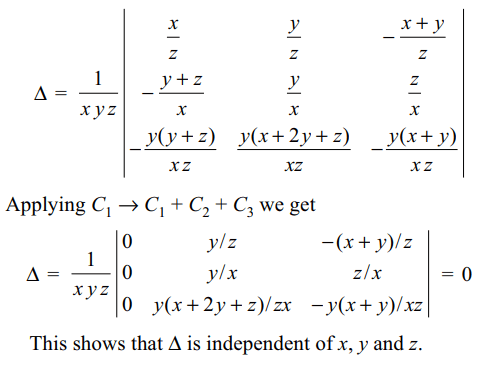
36. Let \[\triangle=\begin{bmatrix}\sin\theta\cos\phi & \sin\theta\sin\phi & \cos\theta \\\cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta \\-\sin\theta\sin\phi & \sin\theta\cos\phi & 0\end{bmatrix}\]
then
a) \[\triangle\] is independent of \[\theta\]
b) \[\triangle\] is independent of \[\phi\]
c) \[\frac{d\triangle}{d\theta}\mid_{\theta =\pi/2}=0\]
d) Both b and c

View Answer

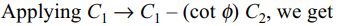
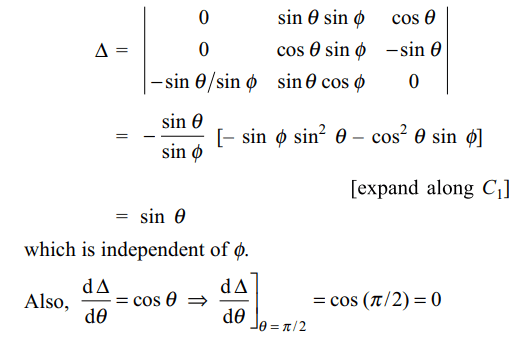
37. Let \[\triangle=\begin{bmatrix}\frac{1}{\sin\theta\cos\phi} & \frac{1}{\sin\theta\sin\phi} & \frac{1}{\cos\theta} \\\frac{-\cos \theta}{\sin^2\theta\cos\phi} & \frac{-\cos \theta}{\sin^2\theta\sin\phi} & \frac{\sin\theta}{\cos^2\theta} \\ \frac{\sin\phi}{\sin\theta\cos^2\phi }& \frac{-\cos\phi}{\sin\theta\sin^2\phi} & 0\end{bmatrix}\]

a) \[\triangle\] is dependent on \[\theta\]
b) \[\triangle\] is dependent on \[\phi\]
c) \[\triangle\] is a constant
d) Both a and b

View Answer

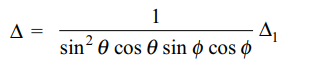
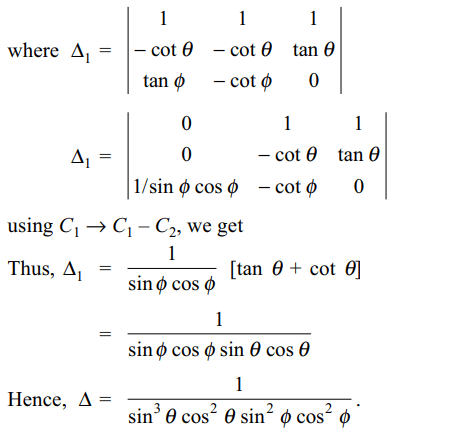
38. The determinant \[\triangle=\begin{bmatrix}a^{2}+x & ab & ac \\ab & b^{2} +x& bc \\ac & bc & c^{2}+x\end{bmatrix}\]
is divisible by
a) x
b) \[x^{2}\]
c) \[a^{2}+b^{2}+c^{2}+x\]
d) All of the above

View Answer

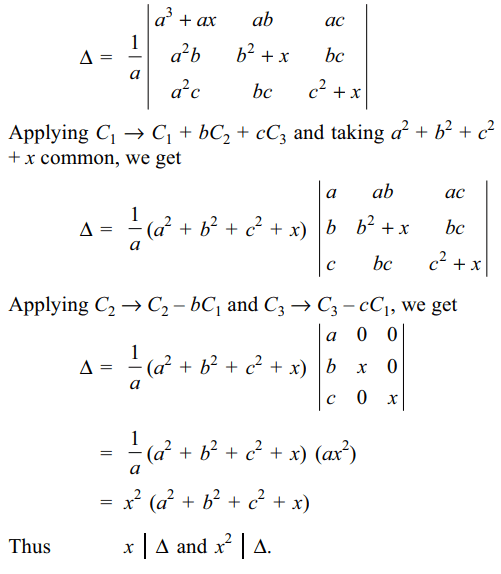
39. Let f(x) \[=\begin{bmatrix}\frac{\pi^{n}}{x} & \sin\pi x & \cos\pi x \\\left(-1\right)^{n}n! & -\sin\left(\frac{n\pi}{2}\right) & -\cos\left(\frac{n\pi}{2}\right) \\-1 & \frac{1}{\sqrt{2}} & \frac{\sqrt{3}}{2}\end{bmatrix}\]
then value of \[\frac{d^{n}}{dx^{n}}\]   [f(x)] at x = 1 is
a) 0
b) independent of x
c) \[\frac{1}{\sqrt{2}}\]
d) Both a and b

View Answer

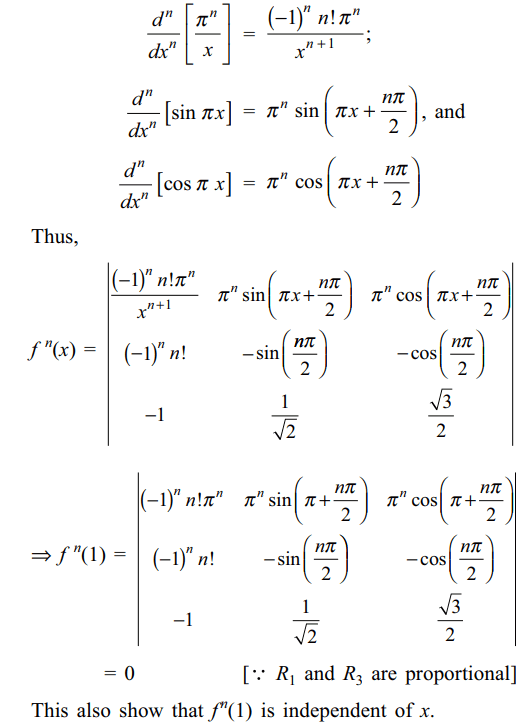
40. If p, q and r are positive integers, and \[\triangle=12\begin{bmatrix}^{p}C_{1} & ^{p}C_{2} & ^{p}C_{3} \\^{q}C_{1} & ^{q}C_{2} & ^{q}C_{3} \\^{r}C_{1} & ^{r}C_{2} & ^{r}C_{3}\end{bmatrix}\]
then
a) \[\triangle\] is an even integer
b) \[\triangle\] is divisible by 12
c) \[\triangle\] is an rational number
d) Both a and c

View Answer

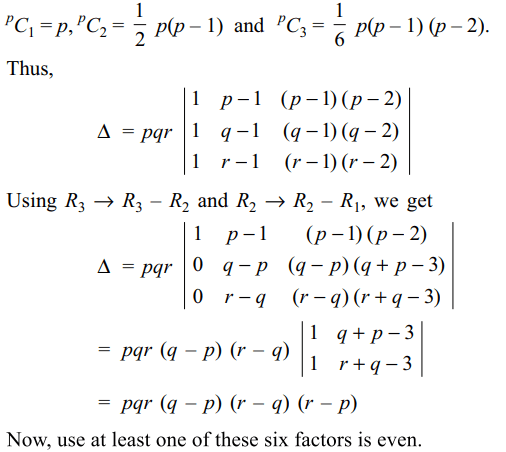
41. if \[f\left(x\right)=\begin{bmatrix}\sec^{2}x & 1 & 1 \\\cos^{2} x & \cos^{2} x & cosec^{2} x \\1 & \cos^{2} x & \cot^{2} x\end{bmatrix}\]
then
a) \[\int_{-\pi/4}^{\pi/4} f\left(x\right)dx=\frac{1}{32}\left(3\pi+8\right)\]
b) \[f'\left(\pi/2\right)=0\]
c) minimun value of \[f\left(x\right)\] is 1
d) All of the above

View Answer

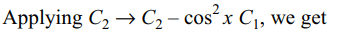
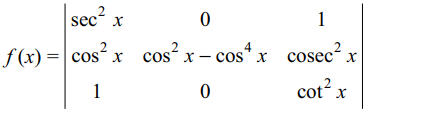
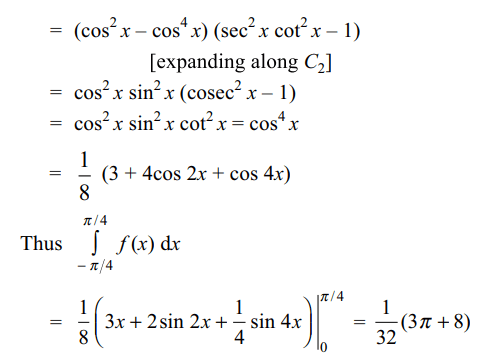
42. Let \[\triangle\left(x\right)=\begin{bmatrix}3 & 3x & 3x^{2}+2a^{2} \\3x & 3x^{2}+2a^{2} & 3x^{3}+6a^{2} x \\3x^{2}+2a^{2} & 3x^{3}+6a^{2} x & 3x^{4}+12a^{2}x^{2}+2a^{4} \end{bmatrix}\]
then
a) \[\triangle\]'(x) = 0
b) \[\triangle\](x) is independent of x
c) \[\int_{0}^{1} \triangle \left(x\right)dx=4a^{6}\]
d) All of the above

View Answer

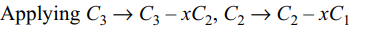
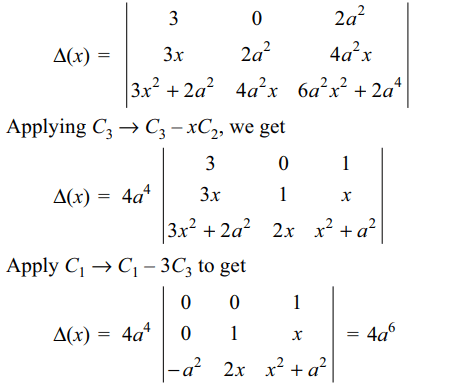
43. Let \[\lambda\] and \[\alpha\] be real. Let S denote the set of all values of \[\lambda\] for which the system of linear equations
\[\lambda x+\left(\sin \alpha\right)y+\left(\cos \alpha\right)z=0\]
\[ x+\left(\cos \alpha\right)y+\left(\sin \alpha\right)z=0\]
\[ -x+\left(\sin \alpha\right)y-\left(\cos \alpha\right)z=0\]
has a non-trivial solution then S contains
a) (– 1, 1)
b) \[\left[-\sqrt{2},-1\right]\]
c) \[\left[1,\sqrt{2}\right]\]
d) All of the above

View Answer

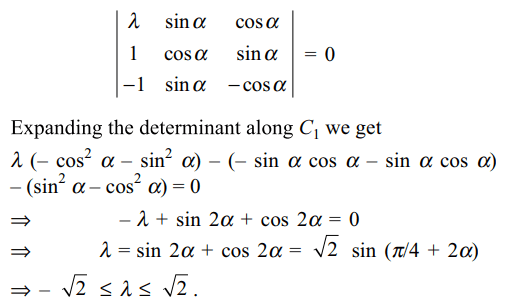
44. Consider the system of linear equations in x, y and z:
(sin 3 \[\theta\] ) x – y + z = 0
(cos 2 \[\theta\] ) x + 4y + 3z = 0
2x + 7y + 7z = 0
The values of \[\theta\] for which the system of equations has a non-trivial solution are
a) \[\left\{{n\pi : n\epsilon I}\right\}\]
b) \[\left\{{m\pi +\left(-1\right)^{m}\pi/6 : m\epsilon I}\right\}\]
c) \[\left\{{n\pi +\left(-1\right)^{n}\pi/3 : n\epsilon I}\right\}\]
d) Both a and b

View Answer

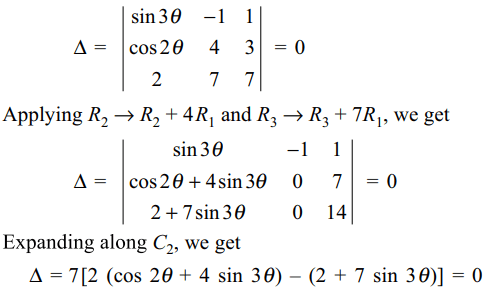
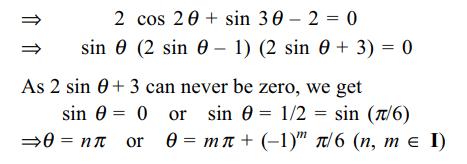
45. Let a, b, c, d be four real numbers and let
\[\triangle=\begin{bmatrix}2 & a+b+c+d & ac+cd \\a+b+c+d & 2\left(a+b\right)\left(c+d\right) & ab\left(c+d\right)+cd\left(a+b\right) \\ab+cd & ab\left(c+d\right)+cd\left(a+b\right) & 2abcd\end{bmatrix}\]
then \[\triangle\] is equal to
a) 2abcd (a + b) (c + d)
b) 2abcd (a + b + c + d)
c) (a + b) (c + d)
d) 0

View Answer

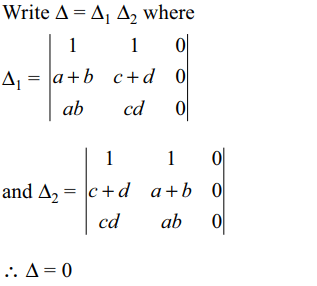
46. If \[\theta\epsilon R\]  maximum value of \[\triangle=\begin{bmatrix}1 & 1 & 1\\1 & 1+\sin\theta & 1 \\1 & 1 & 1+\cos\theta\end{bmatrix}\]
is
a) 1/2
b) \[\sqrt{3}/2\]
c) \[\sqrt{2}\]
d) \[3\sqrt{2}/4\]

View Answer

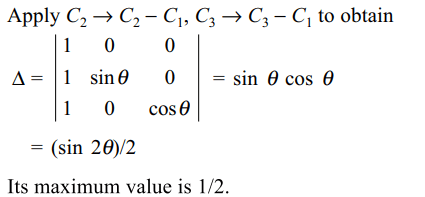
47. if \[\triangle=\begin{bmatrix}x+a& b & c\\a & x+b & c \\a & b & x+c\end{bmatrix}=0\]
then x equals
a) a + b + c
b) – (a + b + c)
c) 0, a + b + c
d) 0, – (a + b + c)

View Answer

48. The determinant \[\triangle=\begin{bmatrix}\sec^{2} \theta& \tan^{2}\theta & 1\\\tan^{2}\theta & \sec^{2}\theta & -1 \\12 & 10 & 2\end{bmatrix}\]
equals
a) \[2\sin^{2} \theta\]
b) \[12\sec^{2} \theta-10\tan^{2} \theta\]
c) \[12\sec^{2} \theta-10\tan^{2} \theta+5\]
d) 0

View Answer

49.Let f and g be two function defined on R such that f(x + y) = f(x) g(y) + g(x) f(y) for each x, \[y\epsilon R\] . Let
\[\triangle=\begin{bmatrix}f\left(\theta+\alpha\right)& f\left(\alpha\right) & g\left(\alpha\right)\\f\left(\theta+\beta\right)& f\left(\beta\right) & g\left(\beta\right) \\f\left(\theta+\gamma\right) & f\left(\gamma\right) & g\left(\gamma\right)\end{bmatrix}\]
then \[\triangle\] equal
a) \[f(\alpha) f(\beta) f(\gamma)\]
b) \[g(\alpha) g(\beta) g(\gamma)\]
c) \[f(\alpha) g(\alpha) + f(\beta) g(\beta) + f(\gamma) g(\gamma)\]
d) 0

View Answer

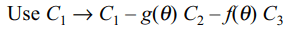
50. If a, \[b\epsilon R\] and \[\triangle=\begin{bmatrix}a & a+bi & bi \\a+bi & bi & a \\bi & a & a+bi \end{bmatrix}\]
then \[\triangle\] equals
a) \[a^{3}+b^{3}i\]
b) \[2\left(a^{3}+b^{3}\right)\]
c) \[a^{3}-b^{3}i\]
d) \[-2\left(a^{3}-b^{3}i\right)\]

View Answer