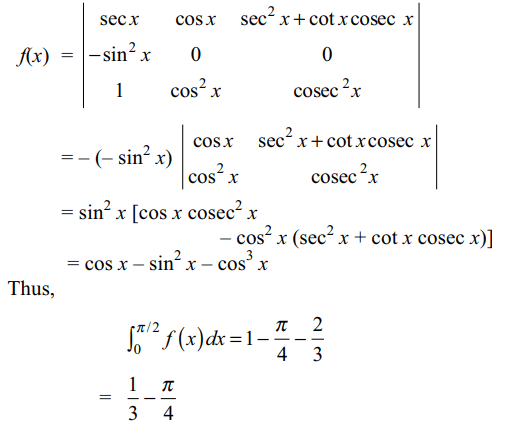1. Let m be a positive integer, a, b, c be
three real numbers and
\[\triangle_{r}=\begin{bmatrix}2r-1 & ^{m}C_{r} & 1 \\m^{2}-1 & 2^m & m+1 \\a & b & c\end{bmatrix}\] \[(0\leq r\leq m)\]
Then the value of
\[\sum_{r=0}^{m}\triangle_{r}\] is given by
a) 0
b) \[m^{2}-1\]
c) \[2^{m}abc\]
d) \[2^{m}\left(a+b+c\right)\]
Explanation: Using the sum property we get
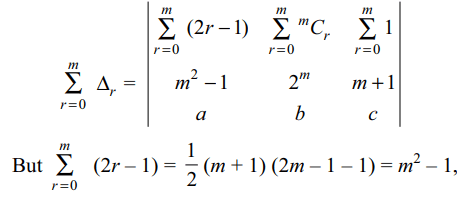
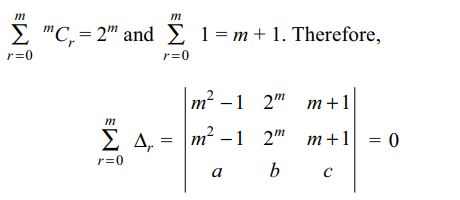
2. If \[\alpha,\beta\] and \[\gamma\] are real numbers, then \[\triangle=\begin{bmatrix}1 & \cos\left(\beta-\alpha\right) & \cos\left(\gamma-\alpha\right) \\\cos\left(\alpha-\beta\right) & 1 & \cos\left(\gamma-\beta\right) \\\cos\left(\alpha-\gamma\right) & \cos\left(\beta-\gamma\right) & 1\end{bmatrix}\]
is equal to
a) -1
b) \[\cos\alpha\cos\beta\cos\gamma\]
c) \[\cos\alpha+\cos\beta+\cos\gamma\]
d) 0
Explanation: We can write \[\triangle\] as a product of two determinants as follows:
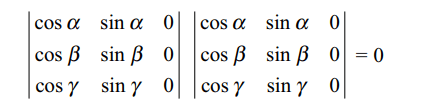
3. If a + b + c > 0, and \[\triangle=\begin{bmatrix}a & b & c \\b & c & a \\c & a & b\end{bmatrix}\] , then
a) \[\triangle< 0\]
b) \[\triangle\leq 0\]
c) \[\triangle> 0\]
d) \[\triangle= 0\]
Explanation: Applying C1 \[\rightarrow\] C1 + C2 + C3, we get
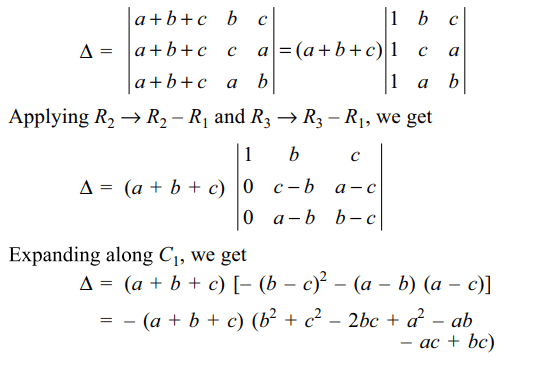
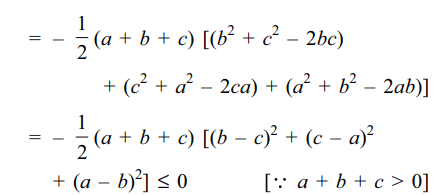
4. If \[p\lambda^{4}+q\lambda^{3}+r\lambda^{2}+s\lambda+t=\begin{bmatrix}\lambda^{2}+3\lambda & \lambda-1 & \lambda+3 \\\lambda^{2}+1 & 2+5\lambda & \lambda-3 \\\lambda^{2}-3 & \lambda+4 & 3\lambda\end{bmatrix}\]
then p is equal to
a) 5
b) 8
c) 3
d) 2
Explanation:
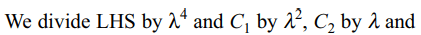

5. If \[\begin{bmatrix}x-1 & 5x & 7 \\x^{2}-1 & x-1 & 8 \\2x &3x & 0\end{bmatrix}=ax^{3}+bx^{2}+cx+d\]
then value of c is given by
a) -1
b) 12
c) 15
d) 17
Explanation: Differentiating both the sides of (1), we get
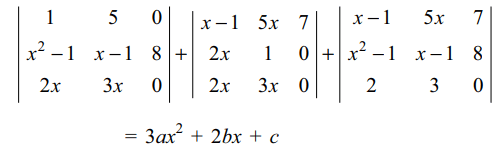
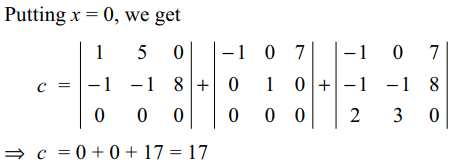
6. If \[l_1^2+m_1^2+n_1^2=1\] , etc., and \[l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}=0\] , etc. and \[\triangle=\begin{bmatrix}l_{1} & m_{1} & n_{1} \\l_{2} & m_{2} & n_{2} \\l_{3} &m_{3} & n_{3}\end{bmatrix}\]
then
a) \[\mid \triangle\mid=3\]
b) \[\mid \triangle\mid=2\]
c) \[\mid \triangle\mid=1\]
d) \[ \triangle=0\]
Explanation:
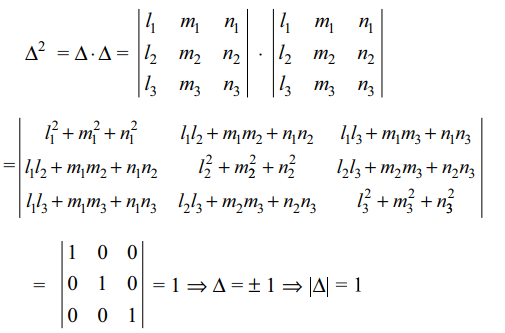
7. The complex number \[Z=\begin{bmatrix}2 & 3+i & -3 \\3-i & 0 & -1+i \\-3&-1-i & 4\end{bmatrix}\]
is equal to
a) 3-4i
b) 5+4i
c) -5i
d) -23
Explanation:
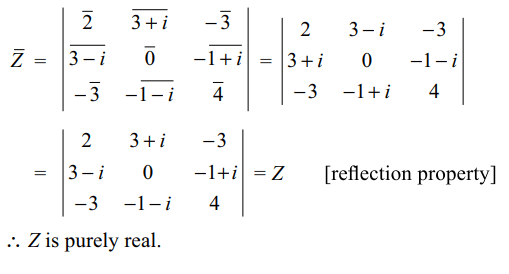
8. If \[a_{1},b_{2},c_{3} \neq 0\]
\[\triangle_{1}=\begin{bmatrix}a^2_{1}+b_{1}+c_{1} & a_{1}a_{2}+b_{2}+c_{2} & a_{1}a_{3}+b_{3}+c_{3} \\b_{1}b_{2}+c_{1} & b^2_{2}+c_{2} & b_{2}b_{3}+c_{3} \\c_{3}c_{1} & c_{3}c_{2} & c^2_{3}\end{bmatrix}\]
and \[\triangle_{2}=\begin{bmatrix}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3}\end{bmatrix}\]
,
then \[\frac{\triangle_{1}}{\triangle_{2}}\] is equal to
a) \[a_{1}b_{2}c_{3} \]
b) \[a_{1}a_{2}a_{3} \]
c) \[a_{3}b_{2}c_{1} \]
d) \[a_{1}b_{1}c_{1} +a_{2}b_{2}c_{2}+a_{3}b_{3}c_{3}\]
Explanation: Taking c3 common from R3 and applying R2 \[\rightarrow\] R2 – R3 and R1 \[\rightarrow\] R1 – R3. We obtain
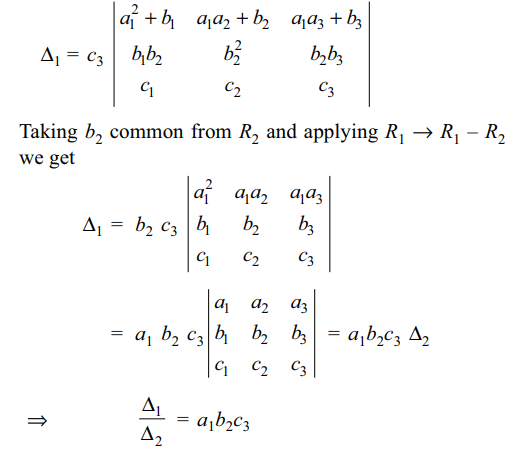
9. For a, b, c, x, y, \[z\epsilon R\] , if
\[\triangle_{1}=\begin{bmatrix}\left(a-x\right)^{2} & \left(b-x\right)^{2} & \left(c-x\right)^{2} \\\left(a-y\right)^{2} & \left(b-y\right)^{2} & \left(c-y\right)^{2} \\\left(a-z\right)^{2} & \left(b-z\right)^{2} & \left(c-z\right)^{2}\end{bmatrix}\]
and \[\triangle_{2}=\begin{bmatrix}\left(1+ax\right)^{2} & \left(1+bx\right)^{2} & \left(1+cx\right)^{2} \\\left(1+ay\right)^{2} & \left(1+by\right)^{2} & \left(1+cy\right)^{2} \\\left(1+az\right)^{2} & \left(1+bz\right)^{2} & \left(1+cz\right)^{2}\end{bmatrix}\]
then
a) \[\triangle_{1}= \triangle_{2}\]
b) \[\triangle_{1}+ \triangle_{2}=0\]
c) \[\triangle_{1}=2\triangle_{2}\]
d) \[\triangle_{1}= -2\triangle_{2}\]
Explanation: We can write the determinant \[\triangle\]1 as product of two determinants as follows:

10. Let f(x) \[=\begin{bmatrix}\sec x & \cos x & \sec^{2}x+\cot x cosec x \\\cos^{2}x & \cos^{2}x & cosec^{2}x \\1 & \cos^{2}x & cosec^{2}x\end{bmatrix}\]
then value of \[\int_{0}^{\pi/2} f\left(x\right)\] dx is
a) 0
b) \[\pi/48\]
c) \[-\frac{\pi}{2}-\frac{\pi}{15\sqrt{2}}\]
d) \[\frac{1}{3}-\frac{\pi}{4}\]
Explanation: Applying R2 \[\rightarrow\] R2 – R3, we get