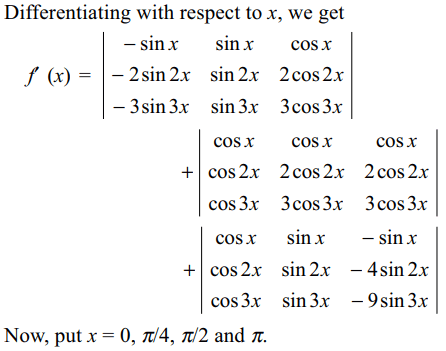1. If \[a_{i}, b_{i}, c_{i} \epsilon R\] (i = 1, 2, 3) and \[x\epsilon R\] and
\[\triangle=\begin{bmatrix}a_{1}+b_{1}x^{2}& a_{1}x^{2}+b_{1} & c_{1} \\a_{2}+b_{2}x^{2} & a_{2}x^{2}+b_{2} & c_{2} \\a_{3}+b_{3}x^{2} & a_{3}x^{2}+b_{3} & c_{3}\end{bmatrix}=0\]
then
a) x=1
b) x=-1
c) \[\begin{bmatrix}a_{1}& b_{1} & c_{1} \\a_{2}& b_{2} & c_{2} \\a_{3} &b_{3} & c_{3}\end{bmatrix}=0\]
d) All of the above
Explanation:
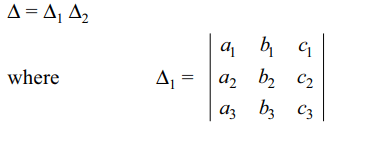
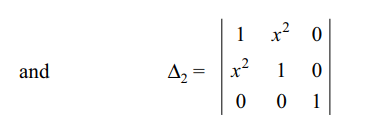
2. The determinant \[\begin{bmatrix}\sin^{2}\alpha&\sin\alpha\cos\alpha & \cos^{2} \alpha\\\sin^{2}\beta& \sin\beta\cos\beta & \cos^{2} \beta \\\sin^{2}\gamma &\sin\gamma\cos\gamma & \cos^{2} \gamma\end{bmatrix}\]
is
a) \[-\sin\left(\beta-\gamma\right)\sin\left(\gamma-\alpha\right)\sin\left(\alpha-\beta\right)\]
b) \[\sin\left(\alpha-\beta\right)\cos\alpha\cos\beta+\sin\left(\beta-\gamma\right)\cos\beta\cos\gamma+\sin\left(\gamma-\alpha\right)\cos\gamma\cos\alpha\]
c) \[\frac{1}{4}\left[sin\left(2\alpha-2\beta\right)+\sin\left(2\beta-2\gamma\right)+\sin\left(2\gamma-2\alpha\right)\right]\]
d) All of the above
Explanation: proving the answer (a). If A + B + C = 0,
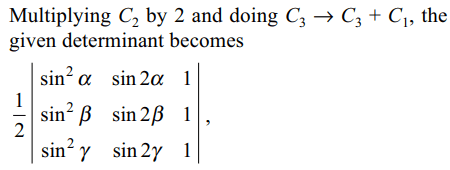
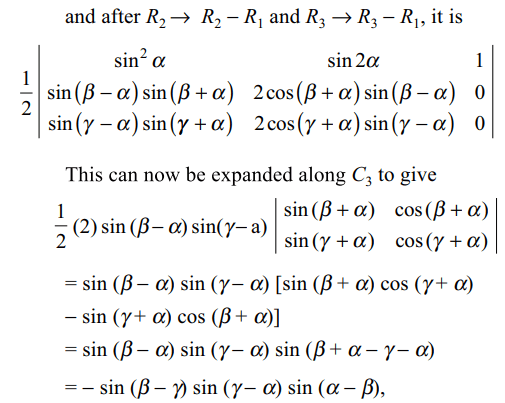
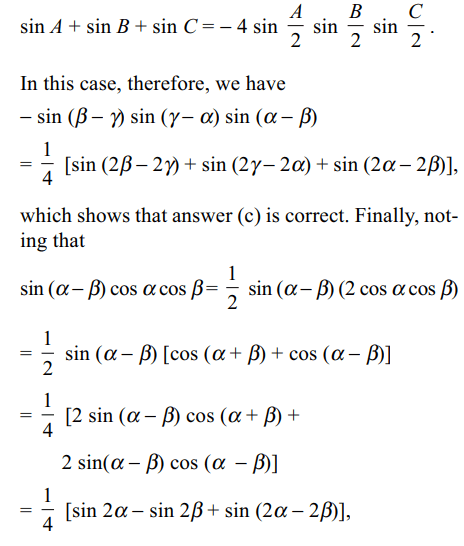
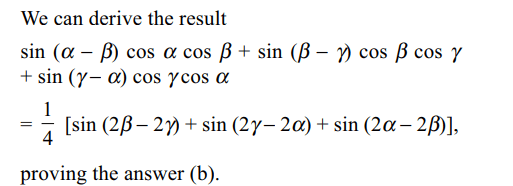
3. If \[a^{2}+b^{2}+c^{2}=1\] , then
\[\begin{bmatrix}a^{2}+\left(b^{2}+c^{2}\right)\cos\phi & ab \left(1-\cos\phi\right) & ac \left(1-\cos\phi\right) \\ba \left(1-\cos\phi\right) & b^{2}+\left(c^{2}+a^{2}\right)\cos\phi & bc \left(1-\cos\phi\right) \\ca \left(1-\cos\phi\right) & cb \left(1-\cos\phi\right) & c^{2}+\left(a^{2}+b^{2}\right)\cos\phi \end{bmatrix}\]
is independent of
a) a
b) b
c) c
d) All of the above
Explanation:
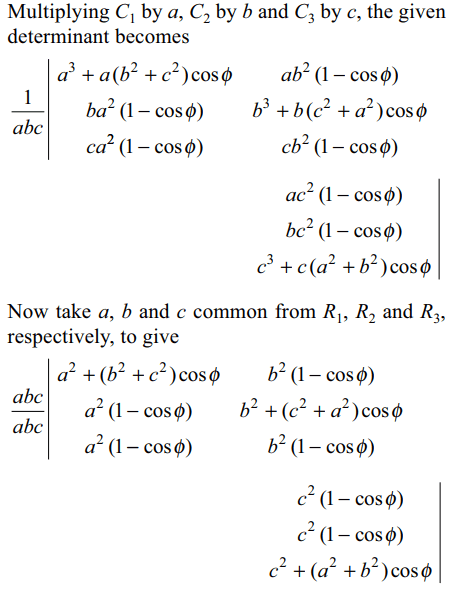
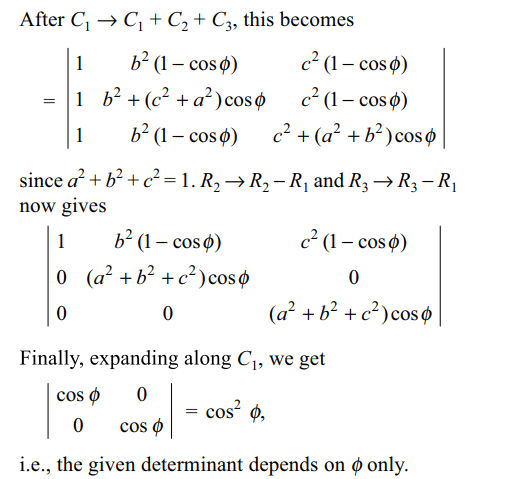
4. If \[\triangle=\begin{bmatrix}\sin\alpha & \cos\alpha & \sin\left(\alpha+\delta\right) \\\sin\beta & \cos\beta & \sin\left(\beta+\delta\right) \\\sin\gamma & \cos\gamma & \sin\left(\gamma+\delta\right) \end{bmatrix}\]
then \[\triangle\] is independent of
a) \[\alpha\]
b) \[\beta\]
c) \[\gamma\]
d) All of the above
Explanation:
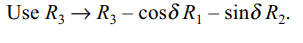
5. If \[\phi\epsilon R\] then
\[\triangle\left(\phi\right)=\begin{bmatrix}\sin \phi & \cos \phi & \sin 2\phi \\\sin\left(\phi +2\pi/3\right) & \cos\left(\phi +2\pi/3\right) & \sin\left(2\phi +4\pi/3\right) \\\sin\left(\phi -2\pi/3\right) & \cos\left(\phi -2\pi/3\right) & \sin\left(2\phi -4\pi/3\right)\end{bmatrix}\]
a) is independent of \[\phi\]
b) is equal to a constant
c) has no local maximum
d) All of the above
Explanation:

6. If \[abc\neq0\] , then
\[\triangle\left(x\right)=\begin{bmatrix}a^{2}\left(1+x\right) & ab & ac \\ab & b^{2}\left(1+x\right) & bc \\ac & bc & c^{2}\left(1+x\right)\end{bmatrix}\]
is divisible by
a) \[3+x\]
b) x
c) \[x^{2}\]
d) All of the above
Explanation:
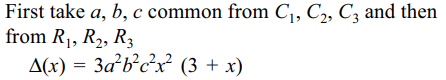
7. If a, b and c are the sides of a triangle and A, B and
C are the angles opposite to a, b and c respectively,
then \[\triangle=\begin{bmatrix}a^{2} & b\sin A & c\sin A \\b\sin A & 1 & \cos A \\c\sin A & \cos A & 1\end{bmatrix}\]
is independent of
a) a
b) b
c) c
d) All of the above
Explanation:
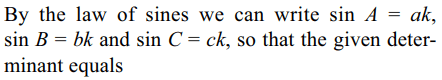
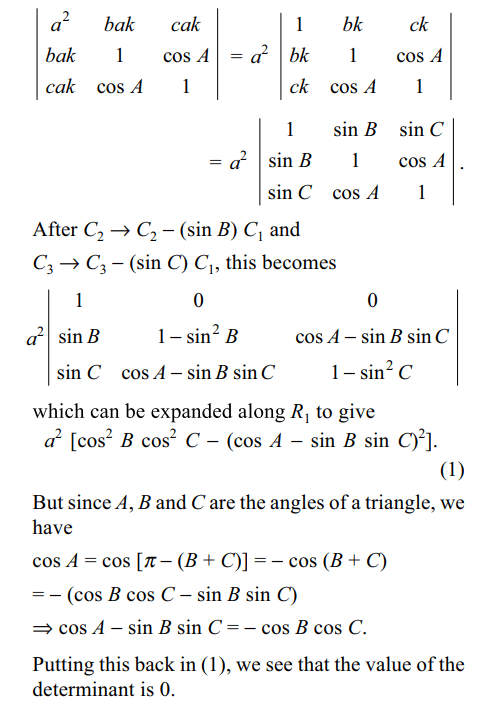
8. If A, B and C are the angles of a triangle and
\[\triangle\left(x\right)=\begin{bmatrix}1 & 1 & 1 \\1+\sin A & 1+\sin B & 1+\sin C \\\sin A+\sin^{2}A & \sin B+\sin^{2}B & \sin C+\sin^{2}C\end{bmatrix}=0\]
then the triangle must be
a) isosceles
b) equilateral
c) right angled
d) none of these
Explanation:

9. If ai, bi ∈ N for i = 1,2,3 then the coefficient of x in
the determinant
\[\begin{bmatrix}\left(1+x\right)^{a_{1}b_{1}} & \left(1+x\right)^{a_{1}b_{2}} & \left(1+x\right)^{a_{1}b_{3}} \\\left(1+x\right)^{a_{2}b_{1}} & \left(1+x\right)^{a_{2}b_{2}} & \left(1+x\right)^{a_{2}b_{3}} \\\left(1+x\right)^{a_{3}b_{1}} & \left(1+x\right)^{a_{3}b_{2}} & \left(1+x\right)^{a_{3}b_{3}}\end{bmatrix}\]
a) 0
b) \[a_{1}+a_{2}+a_{3}\]
c) independent of \[a_{i},s+b_{i},s\]
d) Both a and c
Explanation:
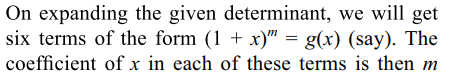
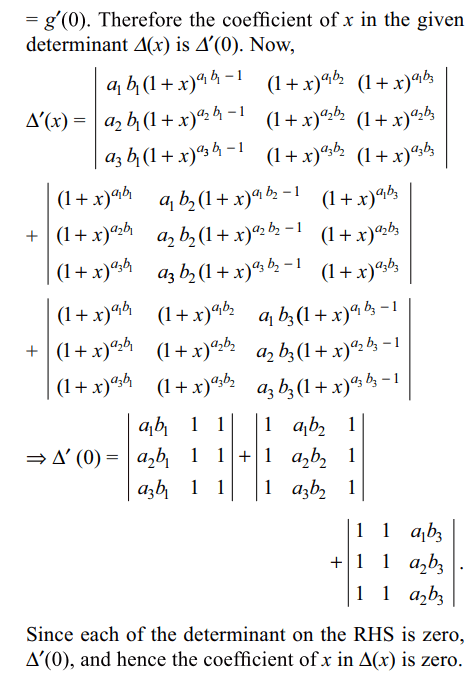
10. Let \[f\left(x\right)=\begin{bmatrix}\cos x & \sin x & \cos x \\\cos 2x & \sin 2x & 2\cos 2x \\\cos 3x & \sin 3x & 3\cos 3x \end{bmatrix}\]
then
a) f '(0) = 0
b) \[f'\left(\pi/2\right)=4\]
c) \[f'\left(\pi\right)=0\]
d) All of the above
Explanation: