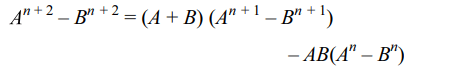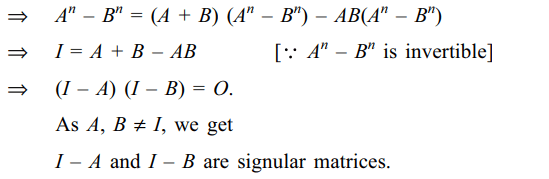PrepBharat

1. Let A, B, C be three 3 * 3 matrices with entries from R such that ABC + AB + BC + AC + A + B + C = O.
a) If A commutes with B + C then A commutes with BC
b) If A commutes with BC then A commutes with B + C
c) A + I is invertible
d) All of the above

View Answer

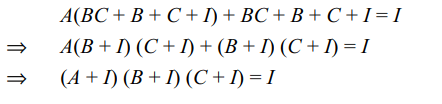
2. Suppose A, B are two distinct \[2 \times2\]   matrices such that
\[A^{2}-5A+6I=0\]
\[B^{2}-5B+6I=0\]
then
a) \[A^{3}-B^{3}=19\left(A-B\right) \]
b) \[A^{4}-B^{4}=65\left(A-B\right) \]
c) \[A^{5}-B^{5}=211\left(A-B\right) \]
d) All of the above

View Answer

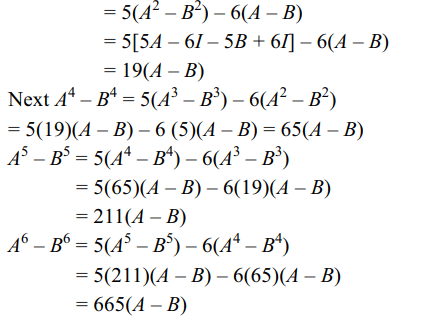
3. Let \[\omega\neq 1\]   be cube root of unity and let P = p_ij be \[n \times n\]  matrix such that \[p_{ij}=\omega^{i+j}\]    . Then \[P^{2}\neq O\]   when n is
a) 56
b) 55
c) 58
d) All of the above

View Answer

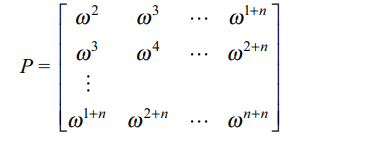
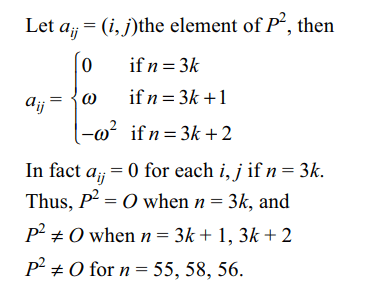
4. Let \[A=\left(a_{ij}\right)_{3\times 3},B=\left(b_{ij}\right)_{3\times 3}\]      be two real symmetric matrices such that \[A^{2}+B^{2}=O\]  , then
a) AB = O
b) A = O
c) B = O
d) All of the above

View Answer

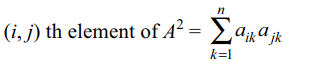
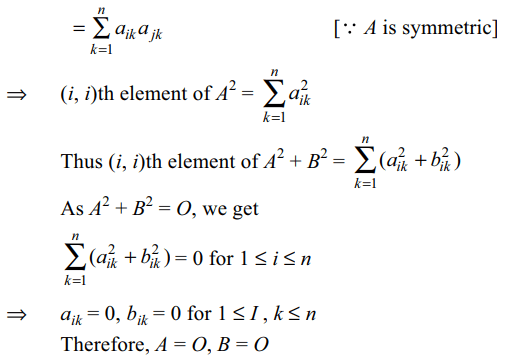
5. Let A be \[4 \times4\]  matrix with real entries such that determinant of every \[2 \times2\]  submatrix is 0, then
a) adj(A) = O
b) det(A) = 0
c) AX = O has infinite number of solutions
d) All of the above

View Answer

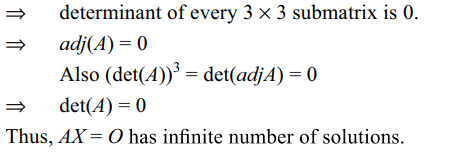
6. Let \[P=\begin{bmatrix}3 & -1 & -2 \\2 & 0 & \alpha \\3 & -5 & 0\end{bmatrix}\]      , where \[\alpha\epsilon R\] , Suppose \[Q=\left[q_{ij}\right]\]   is a matrix such that PQ = kI, where \[k\epsilon R,k\neq 0\]   and I is the identity matrix of order 3. If \[q_{23}=\frac{k}{8}\]   and det\[\left(Q\right)=\frac{k^{2}}{2}\]     , then
a) \[\alpha=0 ,k=8\]
b) \[4\alpha-k+8=0\]
c) det(P adj(Q))= \[2^{9}\]
d) Both b and c

View Answer

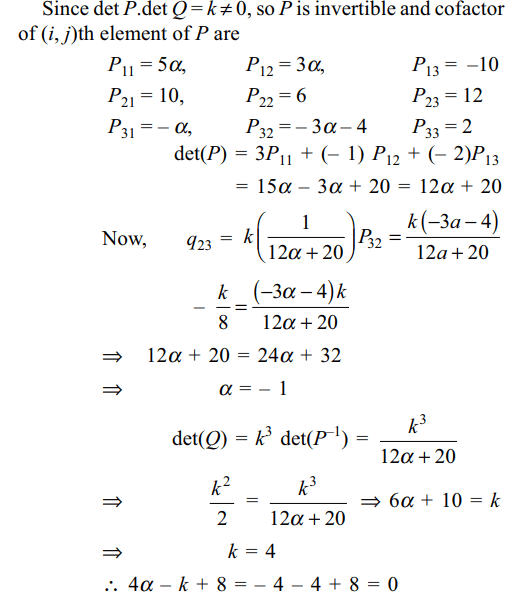
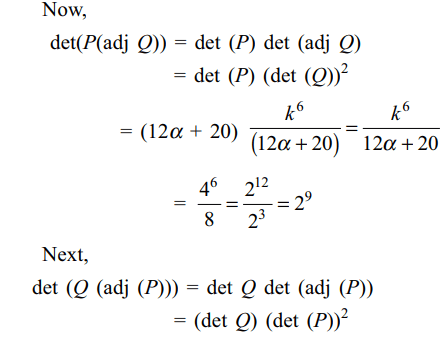
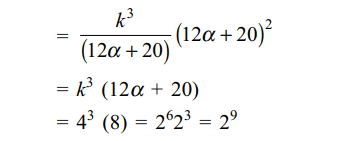
7. Let M be a \[2 \times2\]  symmetric matrix with integer entries. Then M is invertible if
a) the product of entries in the main diagonal of M is not the square of an integer
b) the second row of M is the transpose of the first column of M
c) M is a diagonal matrix with nonzero entries in the main diagonal
d) Both a and c

View Answer

8. Let X and Y be two arbitrary, \[3 \times3\]  , nonzero, skew-symmetric matrices and Z be an arbitrary \[3 \times3\]  , non-zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric?
a) \[X^{23}+Y^{23}\]
b) \[X^{44}+Y^{44}\]
c) \[X^{4}Z^{3}-Z^{3}Y^{4}\]
d) Both a and c

View Answer

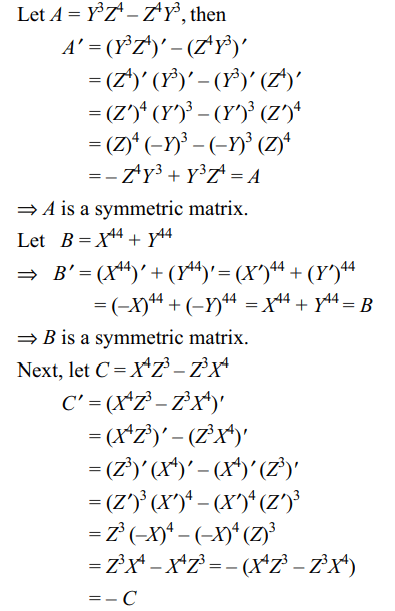
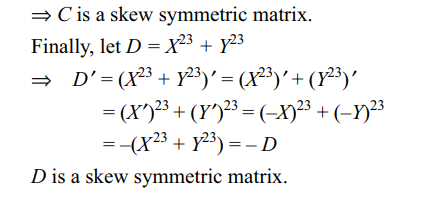
9. Let A, B be two \[2 \times2\]  real commutative matrices, such that det \[\left(A^{2}+AB+B^{2}\right)=0\]     , then
a) \[det \left(A-\omega B\right)=0\]
b) \[det \left(A-\omega^{2} B\right)=0\]
c) \[det \left(A+ B\right)=0\]
d) Both a and b

View Answer

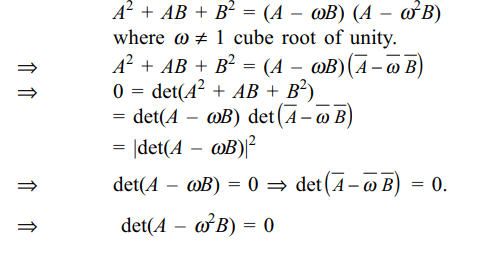
10. Let A and B be two matrices different from I such that AB = BA and Aⁿ – Bⁿ is invertible for some positive integer n. If \[A^{n}-B^{n}=A^{n+1}-B^{n+1}=A^{n+2}-B^{n+2}\]        , then
a) I – A is singular
b) I – B is singular
c) A + B = AB + I
d) All of the above

View Answer