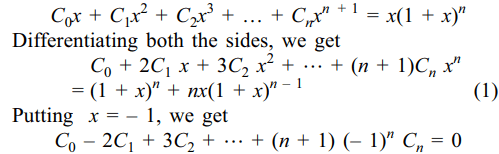1. Suppose m and n are positive integers
and let
\[S=\sum_{k=0}^{n}\left(-1\right)^{k}\frac{1}{k+m+1}\left(^{n}C_{k}\right)\]
and \[T=\sum_{k=0}^{n}\left(-1\right)^{k}\frac{1}{k+n+1}\left(^{m}C_{k}\right)\]
then S-T is equal to
a) 0
b) \[n^{m}-m^{n}\]
c) \[\left(n+1\right)^{m}-\left(m+1\right)^{n}\]
d) \[\left(1-n\right)^{m}-\left(1-m\right)^{n}\]
Explanation:
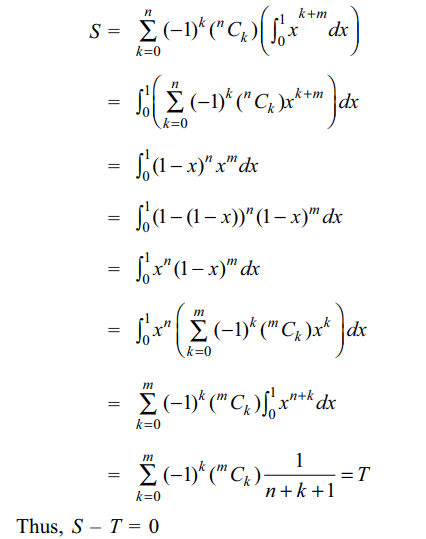
2. Let \[S=\sum_{r=0}^{n}\frac{^{n}C_{r}}{\sum_{s=0}^{r}\frac{^{s}C_{r}}{\sum_{t=0}^{s}.^{s}C_{t}\left(2\sin \frac{\pi}{10}\right)^{t}}}\]
Then \[S^{1/n}\] is equal to
a) \[2\cos\left(\pi/5\right)\]
b) \[2\cos\left(\pi/10\right)\]
c) \[2\sin\left(\pi/5\right)\]
d) \[2\sin\left(\pi/10\right)\]
Explanation:
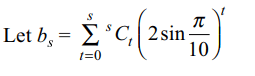
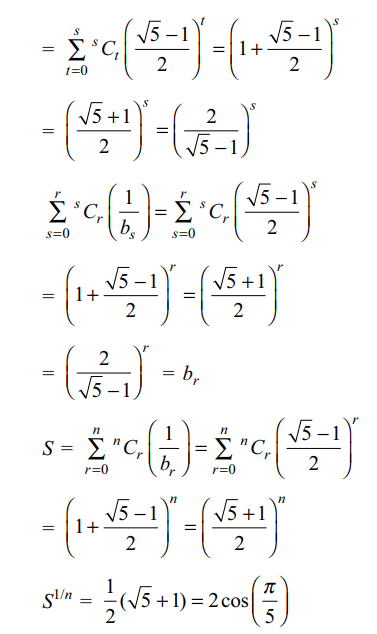
3. Let P(x) be a polynomial with real
coefficients such that \[\int_{0}^{1}x^{m}P \left(1-x\right)dx=0 \forall m \epsilon N\cup\left\{0\right\}\]
,then
a) \[P \left(x\right)=x^{n}\left(1-x\right)^{n}\] for some \[n\epsilon N\]
b) \[P \left(x\right)=\left(1-x\right)^{2n}\] for some \[n\epsilon N\]
c) \[P \left(x\right)=1-x^{m}\left(1-x\right)^{n}\] for some m, \[n\epsilon N\]
d) P(x) \[\equiv\] 0
Explanation:
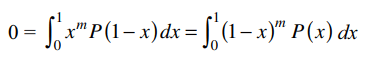
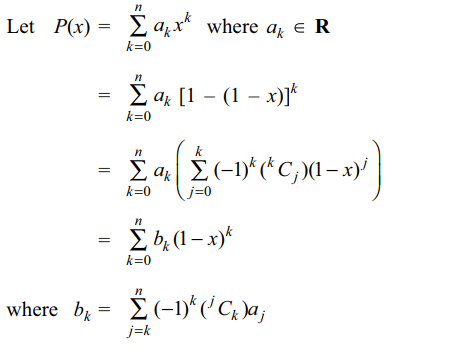
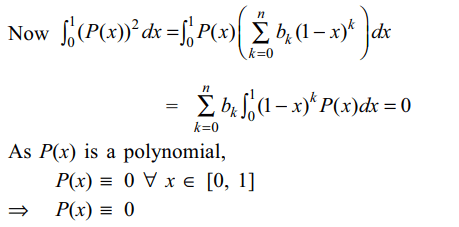
4. Suppose [x] denote the greatest integer
\[\leq x\] , and \[n\epsilon N\] , then
\[\lim_{n \rightarrow \infty}\frac{\left[^{n}C_{0}x^{2}\right]+\left[^{n}C_{1}x^{2}\right] +....+\left[^{n}C_{n}x^{2}\right]}{2^{n}-2}\]
a) \[\frac{1}{2}x^{2}\]
b) \[x^{2}\]
c) \[2x^{2}\]
d) \[4x^{2}\]
Explanation:
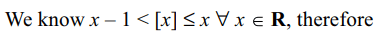
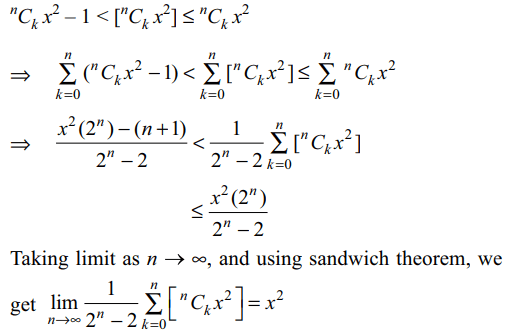
5. If in the expansion of \[\left(a-2b\right)^{n}\] , the sum of
5th and 6th term is 0, then value of \[\frac{a}{b}\]
is
a) \[\frac{n-4}{5}\]
b) \[\frac{2(n-4)}{5}\]
c) \[\frac{5}{n-4}\]
d) \[\frac{5}{2(n-4)}\]
Explanation:
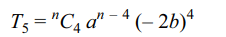
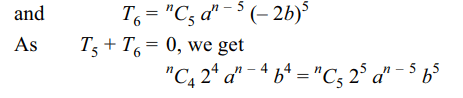
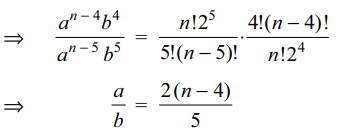
6. The coefficient of \[t^{50}\] in
\[\left(1+t^{2}\right)^{25}\left(1+t^{25}\right)\left(1+t^{40}\right)\left(1+t^{45}\right)\left(1+t^{47}\right)\] (1)
is
a) \[1+^{25}C_{5}\]
b) \[1+^{25}C_{5}+^{25}C_{7}\]
c) \[1+^{25}C_{7}\]
d) 1
Explanation: As we are interested in coefficient of t50, we shall ignore all the term with exponent more than 50
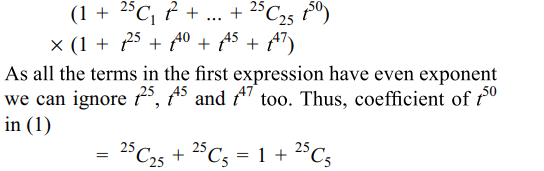
7. The expression \[P\left(x\right)=\left(\sqrt{x^{5}-1}+x\right)^{7}-\left(\sqrt{x^{5}-1}-x\right)^{7}\]
is a polynomial of degree
a) 16
b) 18
c) 20
d) 27
Explanation:
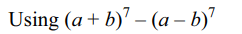
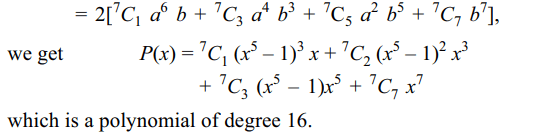
8. The expression \[\left(\sqrt{2x^{2}+1}+\sqrt{2x^{2}-1}\right)^{6}+\left(\frac{2}{\left(\sqrt{2x^{2}+1}\right)+\left(\sqrt{2x^{2}-1}\right)}\right)^{6}\]
is a polynomial of degree
a) 6
b) 8
c) 10
d) 12
Explanation:
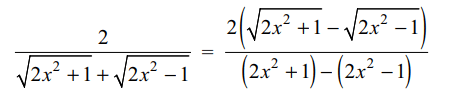
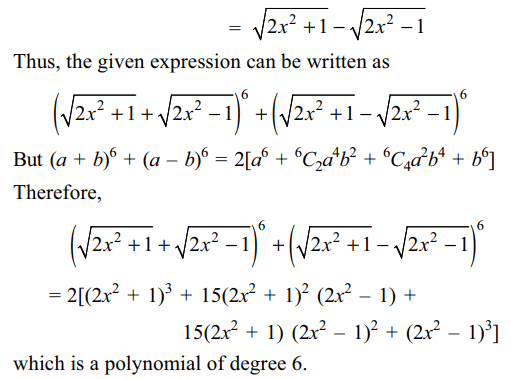
9. The expression \[C_{0}+2C_{1}+3C_{2}+....+\left(n+1\right)C_{n}\] is equal to
a) \[2^{n-1}\]
b) \[n\left( 2^{n-1}\right)\]
c) \[n\left( 2^{n-1}\right)+2^{n}\]
d) \[\left( n+1\right)2^{n}\]
Explanation:
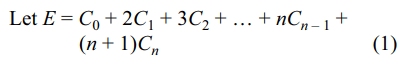
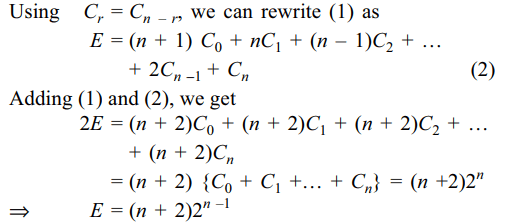
10. If n > 1 then value of the expression is \[C_{0}-2C_{1}+3C_{2}-4C_{3}+....+\left(-1\right)^{n}\left(n+1\right)C_{n}\]
is
a) -1
b) 0
c) 1
d) none of these
Explanation: