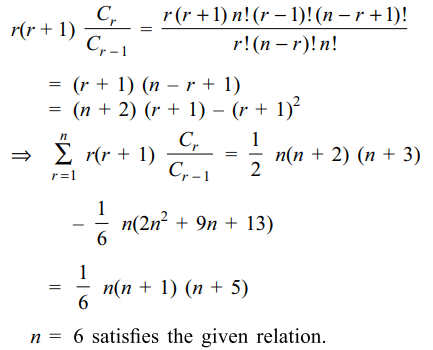1. If \[\left(1+x+x^{2}\right)^{n}=a_{0}+a_{1}x+a_{2}x^{2}+....+a_{2n}x^{2n}\] , then
value of \[N=a_{0}a_{1}-a_{1}a_{2}+a_{2}a_{3}-a_{3}a_{4}+....\] is equal
to
a) 0
b) n
c) -n
d) 1
Explanation:
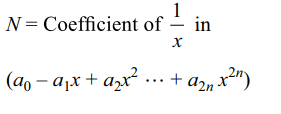
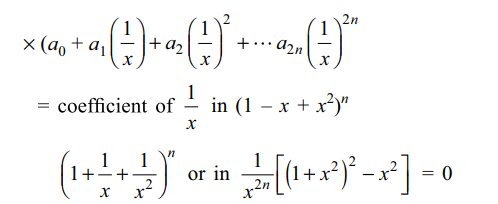
2. If three succesive coffiecients in the exapansion of \[\left(1+x\right)^{n}\] are in A.P., then (n + 2) is
a) at least 19
b) at most 19
c) a prefect square
d) a prefect cube
Explanation:
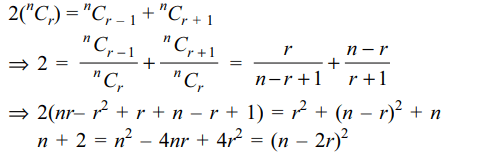
3. Sum of the first 20 terms of the series
\[\frac{1}{\left(2\right)\left(4\right)}+\frac{\left(1\right)\left(3\right)}{\left(2\right)\left(4\right)\left(6\right)}+\frac{\left(1\right)\left(3\right)\left(5\right)}{\left(2\right)\left(4\right)\left(6\right)\left(8\right)}+....\]
is
a) \[\frac{1}{2}-\frac{1}{2^{40}}\left(^{40}C_{20}\right)\]
b) \[\frac{1}{2}-\frac{1}{2^{41}}\left(^{42}C_{21}\right)\]
c) \[\frac{1}{2}-\frac{1}{2^{42}}\left(^{42}C_{21}\right)\]
d) \[\frac{1}{2}-\frac{1}{2^{43}}\left(^{40}C_{20}\right)\]
Explanation:
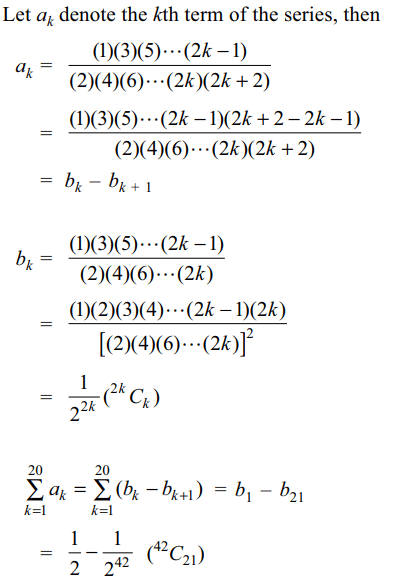
4. Coefficients of \[x^{n}\] in the expression \[\left(1-2x+3x^{2}-4x^{3}+....\right)^{-n}\]
equals
a) \[^{2n}C_{n}\]
b) \[^{2n}C_{n+1}\]
c) \[^{3n}C_{n}\]
d) 0
Explanation:
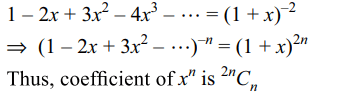
5. If \[a=99^{100},b=100^{99}\] , then
a) a > b
b) a=b
c) a < b
d) \[a+2b=101^{100}\]
Explanation:
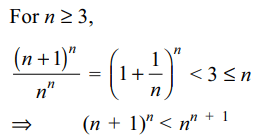
6. If \[\alpha\epsilon\left[-1,1\right]\] and \[I\left(\alpha\right)\] denotes the term independent
of x in the expansion of
\[\left(x\sin ^{-1}\alpha+\frac{1}{x}\cos^{-1}\alpha\right)^{10}\]
then \[\mid I \left(\alpha\right)\mid\] cannot exceed
a) \[\frac{1}{2^{10}}\]
b) \[^{10}C_{5}\frac{\pi^{5}}{2^{10}}\]
c) \[^{10}C_{5}\frac{\pi^{10}}{2^{20}}\]
d) \[^{10}C_{5}\left(\frac{1}{2}\right)^{10}\]
Explanation:
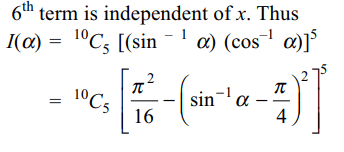
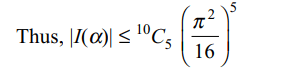
7. For \[n\epsilon N\] , \[x\epsilon R\] , the sum of the series \[C_{1}x\left(1-x\right)^{n-1}+2C_{2}x^{2}\left(1-x\right)^{n-2}+3C_{3}x^{3}\left(1-x\right)^{n-3}+...+nC_{n}x^{n}\]
is
a) nx
b) 0
c) \[2^{n}x\]
d) \[n2^{n-1}x\]
Explanation:
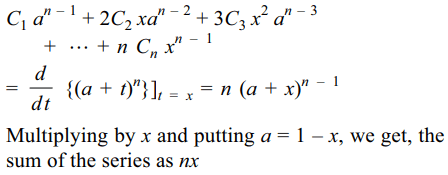
8. Let \[a_{n}=\sum_{k=0}^{n}\left(1+2^{k}\right)C_{k}\] then which of the following
an equals \[a_{n+1}\]
a) \[5a_{n}-6a_{n-1}\]
b) \[5a_{n}+6a_{n}\]
c) \[2a_{n}+3a_{n-1}\]
d) \[a_{n}+a_{n-1}\]
Explanation:
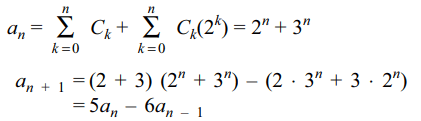
9. If \[\log x=\log _{10}x\] , the values of x for which 4th term
in the expansion of
\[\left[\sqrt{x^{2/\left(1+\log x\right)}}+x^{1/12}\right]^{6}\]
is 200 are
a) 0.001, 0.1
b) 0.0001, 10
c) 0.01, 100
d) 0.1, 10000
Explanation:
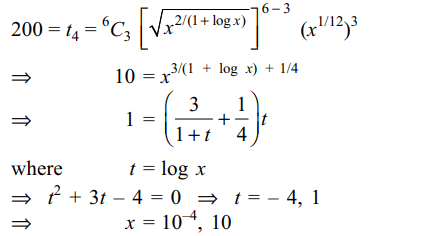
10. If \[\sum_{r=1}^{n}r\left(r+1\right)\frac{C_{r}}{C_{r-1}}=77\] , then n equals
a) 5
b) 6
c) 7
d) 11
Explanation: