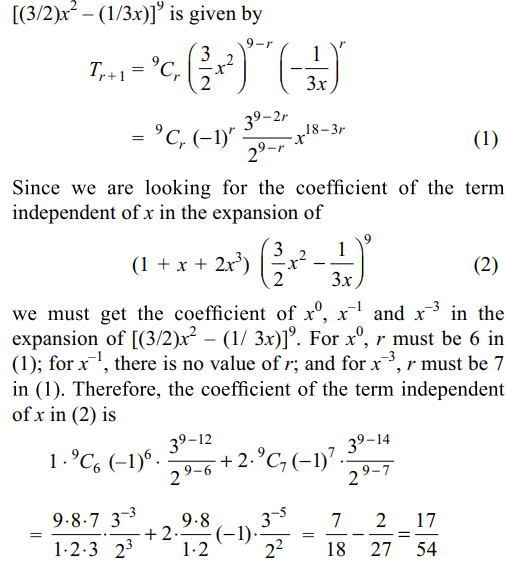1. Sum of the last 30 coefficients in the
expansion of \[\left(1+x\right)^{59}\] , when expanded in ascending powers
of x, is
a) \[2^{29}\]
b) \[2^{28}\]
c) \[^{60}C_{30}2^{19}\]
d) \[2^{58}\]
Explanation: There are 60 terms in the expansion of
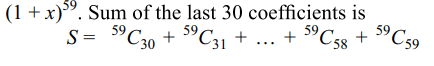
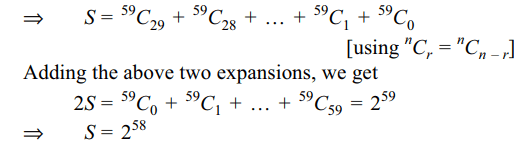
2. The sum of the rational terms in the
expansion of \[\left(2^{1/5}+\sqrt{3}\right)^{20}\] is
a) 71
b) 85
c) 97
d) none of these
Explanation:
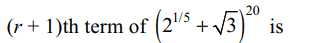

3. If sum of the coefficients of the first , second and third terms of the expansion
of \[\left(x^{2}+\frac{1}{x}\right)^{m}\] is 46,then the coefficients of the term that does not contain
x is
a) 84
b) 92
c) 98
d) 106
Explanation:
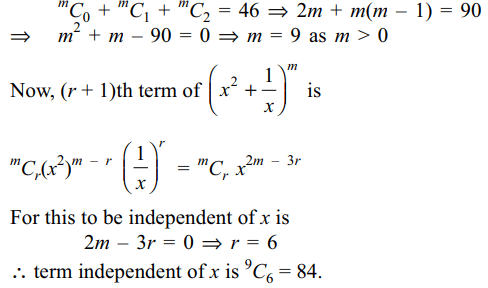
4. Value of \[\sum_{k=1}^{n}\left(C_{k}\right)\left(C_{k-1}\right)\] is
a) \[^{2n}C_{n}\]
b) \[\frac{1}{2}\left(^{2n+2}C_{n+1}\right)-^{2n}C_{n}\]
c) \[^{2n}C_{n+2}\]
d) \[^{2n}C_{n+1}\]
Explanation:
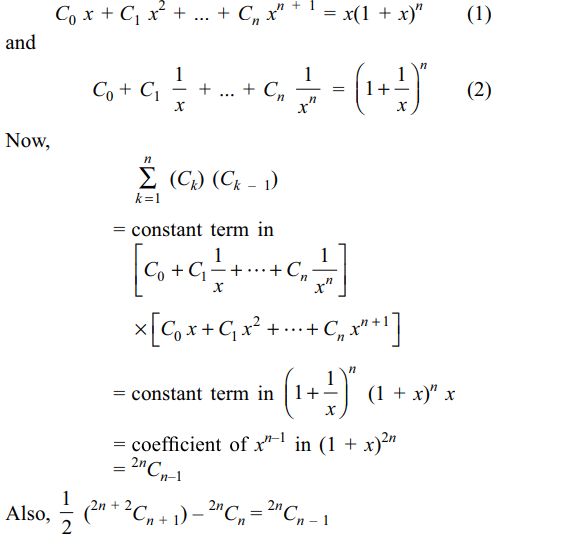
5. Value of \[S = 1 \times 2 \times 3 \times 4 + 2 \times 3 \times 4 \times 5
+ .... + n (n + 1) (n + 2) (n + 3)\]
is
a) \[\frac{1}{5}n\left(n+1\right)\left(n+2\right)\left(n+3\right)\left(n+4\right)\]
b) \[\frac{1}{5!}\left(^{n+3}C_{5}\right)\]
c) \[\frac{1}{5}\left(^{n+4}C_{4}\right)\]
d) \[\frac{1}{5}\left(^{n}C_{4}\right)\]
Explanation:
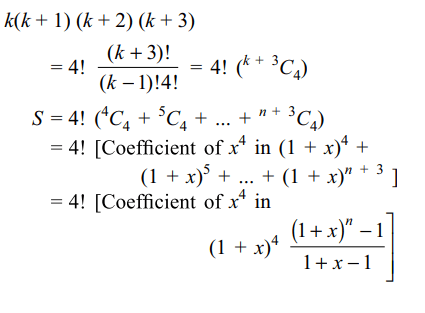
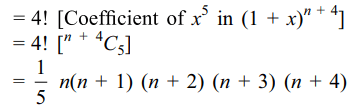
6. If in the expansion of \[\left(x^{3}-\frac{1}{x^{2}}\right)^{n}\] , \[n\epsilon N\] ,
sum of the coefficient of \[x^{5}\] and \[x^{10}\] is 0, then value
of n is
a) 5
b) 10
c) 15
d) 20
Explanation: (r + 1)th term in the expansion of
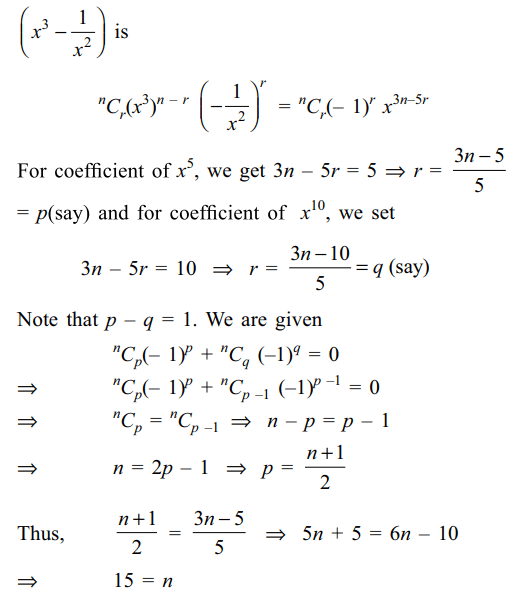
7. If the last term in the binomial expansion
of \[\left(2^{1/3}-\frac{1}{\sqrt{2}}\right)^{n}\] is
\[\left(\frac{1}{3^{5/3}}\right)^{\log_{3}8}\] , then the 5th term from the
beginning is
a) 210
b) 420
c) 105
d) 35
Explanation:
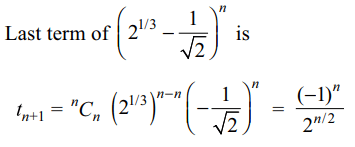
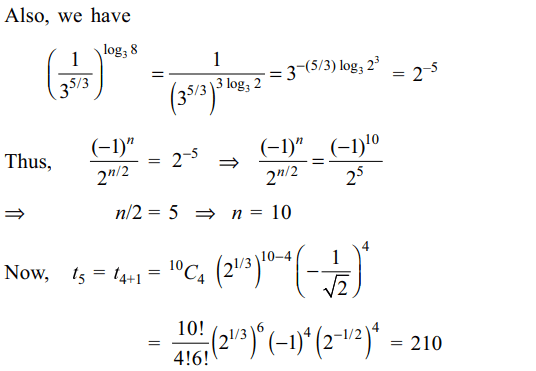
8. If coefficients of \[x^{20}\] in \[\left(1-x+x^{2}\right)^{20}\]
and in \[\left(1+x-x^{2}\right)^{20}\] are respectively a and b, then
a) a = b
b) a > b
c) a < b
d) a+b=0
Explanation:
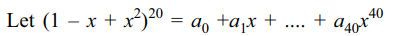
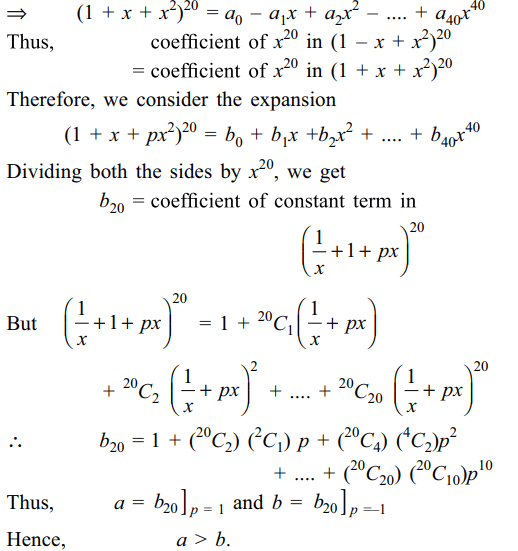
9. if coefficients of 2nd ,3rd and the 4th terms in the expansion of \[\left(1+x\right)^{n}\] are in
A.P., then value of n is
a) 5
b) 7
c) 11
d) 14
Explanation:
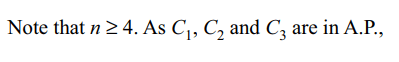
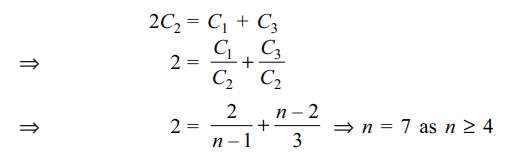
10. The coefficient of the term independent of x in the expansion of \[\left(1+x+2x^{3}\right)\left(\frac{3}{2}x^{2}-\frac{1}{3x}\right)^{9}\]
is
a) 1/3
b) 19/54
c) 17/54
d) 1/4
Explanation: The (r + 1)th term in the expansion of