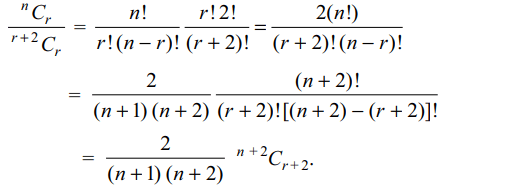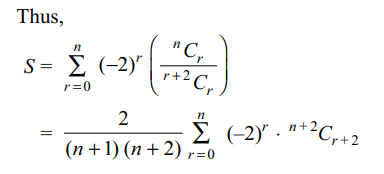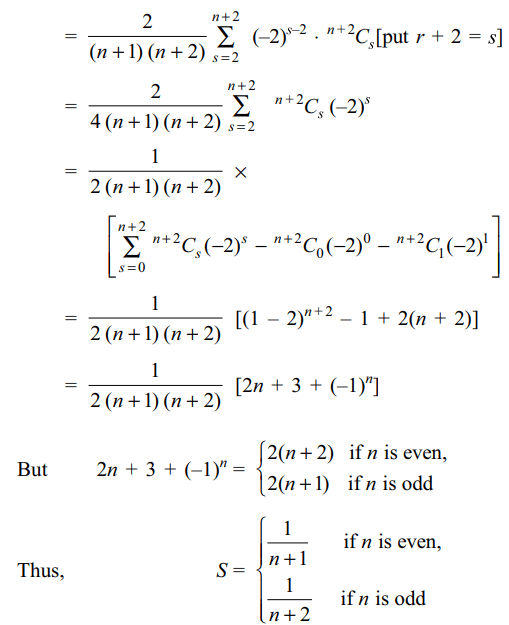1. If the third term in the expansion of
\[\left[\left(1/x\right)+x^{\log}10^{x}\right]^{5}\] is 1000, then x is equal to
a) 100
b) 10
c) \[1/\sqrt{10}\]
d) Both a and c
Explanation:
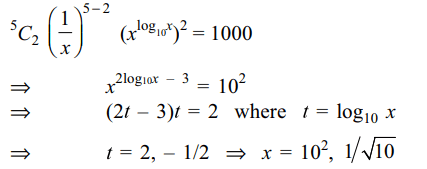
2. If the third term in the expansion of \[\left(x+x^{\log10x}\right)^{5}\] is \[10^{6}\] , then x can be
a) \[10^{-1/3}\]
b) 10
c) \[10^{-5/2}\]
d) Both b and c
Explanation:
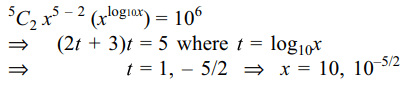
3. Positive integer (s) which is (are) greater than
\[\left(1+0.0001\right)^{10000}\] is (are)
a) 3
b) 4
c) 5
d) All of the above
Explanation: Use the fact that
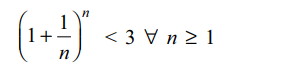
4. If \[\left(1+2x+3x^{2}\right)^{10}=a_{0}+a_{1}x+a_{2}x^{2}+....+a_{20}x^{20}\]
then
a) \[a_{1}=20\]
b) \[a_{2}=210\]
c) \[a_{4}=8085\]
d) All of the above
Explanation:
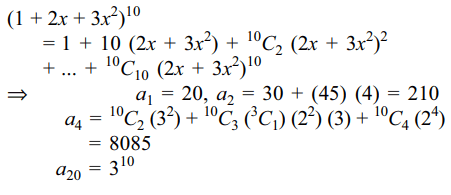
5. The number \[101^{100}-1\] is divisible by
a) 100
b) 1000
c) 10000
d) All of the above
Explanation:
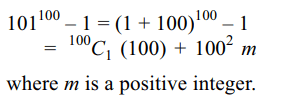
6. If the second, third and fourth terms in the expansion
of \[\left(a+b\right)^{n}\] are 135, 30 and 10/3 respectively,
then
a) a=3
b) b=1/3
c) n=5
d) All of the above
Explanation:

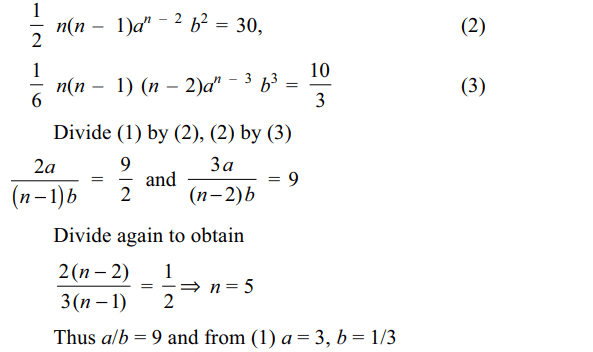
7. The coefficient of the middle term in the expansion of \[\left(1+x\right)^{2n}\] is
a) \[^{2n}C_{n}\]
b) \[\frac{1.3.5....\left(2n-1\right)}{n!}{2^{n}}\]
c) \[2 \times 6....\left(4n-2\right)\]
d) Both a and b
Explanation:
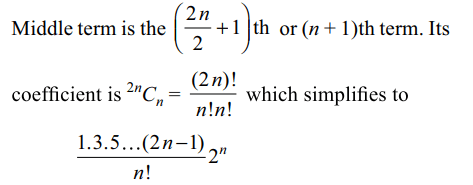
8. If n > 1, then \[\left(1+x\right)^{n}-nx-1\] is divisible by
a) x
b) \[x^{2}\]
c) \[x^{3}\]
d) Both a and b
Explanation:
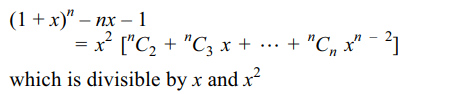
9. If the middle term of
\[\left(x+\frac{1}{x}\sin^{-1}x\right)^{8}\] is equal to 630/16 , then value of x is (are)
a) \[\pi/3\]
b) \[\pi/6\]
c) \[-\pi/3\]
d) Both a and c
Explanation:
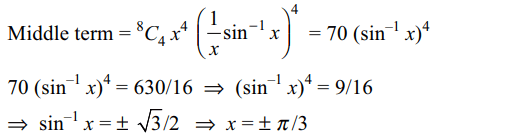
10. Let \[S_{n}=\sum_{r=0}^{n}\left(-2\right)^{r}\left(\frac{^{n}C_{r}}{^{r+2}C_{r}}\right)\] then
a) \[S_{n}=\frac{1}{n+1}\] if n is odd
b) \[S_{n}=\frac{1}{n+2}\] if n is odd
c) \[S_{n}=\frac{1}{n+1}\] if n is even
d) Both b and c
Explanation: