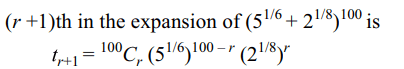1. Value of the expression \[C_0^2+C_1^2+C_2^2+....+C_n^2\] is
a) \[2^{2n-1}\]
b) \[2n\left(^{2n}C_{n}\right)\]
c) \[^{2n}C_{n}\]
d) none of these
Explanation:
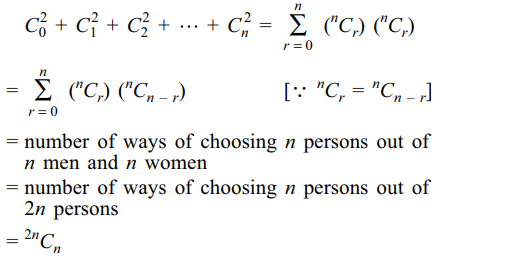
2. Value of the expression \[C_0^2+2C_1^2+....+\left(n+1\right)C_n^2\] is
a) \[\left(2n+1\right)\left(^{2n}C_{n}\right)\]
b) \[\left(2n-1\right)\left(^{2n}C_{n}\right)\]
c) \[\left(\frac{n}{2}+1\right)\left(^{2n}C_{n}\right)\]
d) \[\left(\frac{n}{2}+1\right)\left(^{2n-1}C_{n}\right)\]
Explanation:
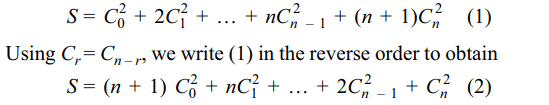
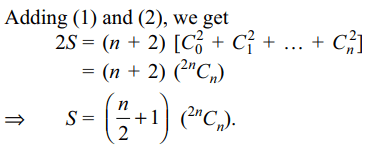
3. If \[n\epsilon N\], then value of \[S=\sum_{r=0}^{n}\left(-1\right)^{r}\frac{\left(^{n}C_{r}\right)}{\left(^{r+2}C_{r}\right)}\] is
a) \[\frac{1}{n+2}\]
b) \[\frac{2}{n+2}\]
c) n+2
d) n+1
Explanation:
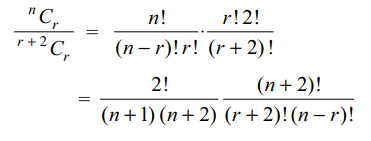
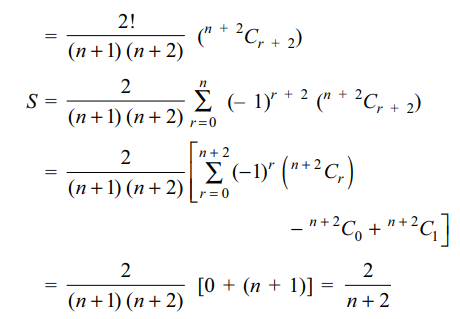
4. For \[n\epsilon N\], let \[S(n)=\sum_{r=0}^{n}\left(-1\right)^{r}\frac{1}{^{n}C_{r}}\]
value of \[S=\sum_{r=0}^{n}\left(-1\right)^{r}\frac{^{r+2}C_{r}}{^{n}C_{r}}\] is
a) \[S\left(n+2\right)-\frac{1}{2}\left(n+1\right)^{2}\]
b) \[S\left(n+2\right)+\frac{1}{2}\left(n+1\right)^{2}\]
c) 0
d) none of these
Explanation: From Q3,
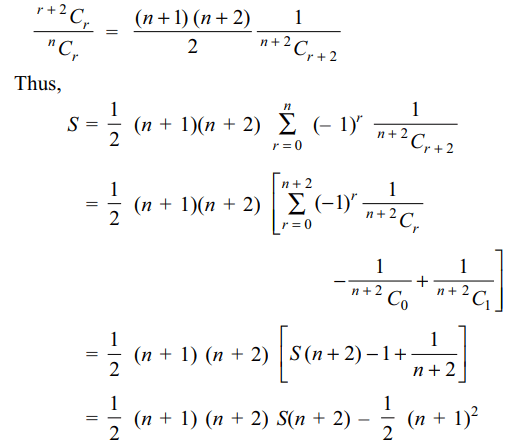
5. If \[\sum_{r=0}^{2n}a_{r}\left(x-100\right)^{r}=\sum_{r=0}^{2n}b_{r}\left(x-101\right)^{r}\]
and \[a_{k}=\frac{2^{k}}{^{k}C_{n}}\forall k\geq n\] , then \[b_{n}\] equals
a) \[2^{n}\left(2^{n+1}-1\right)\]
b) \[2^{n}\left(2^{n}+1\right)\]
c) \[2^{n}\left(2^{n}-1\right)\]
d) \[2^{n+1}\left(2^{n}-1\right)\]
Explanation: Put x – 101 = t, so that
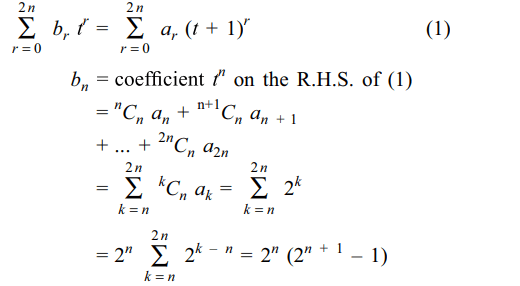
6. If n is even, then value of the expression \[C_0^2-\frac{1}{2}C_1^2+\frac{1}{3}C_2^2- ....+\frac{\left(-1\right)^{n}}{n+1}C_n^2\]
where
\[C_r= ^{n}C_{r} \] is
a) \[\frac{\left(-1\right)^{n}n!}{\left(n+1\right)\left(n/2\right)!^{2}}\]
b) \[\frac{\left(-1\right)^{n-1}n!}{\left(n+1\right)\left(n/2\right)!^{2}}\]
c) \[\frac{-1}{\left(n+1\right)\left(n/2\right)!^{2}}\]
d) \[\frac{-1^{n/2}n!}{\left(n+1\right)\left(n/2\right)!^{2}}\]
Explanation:
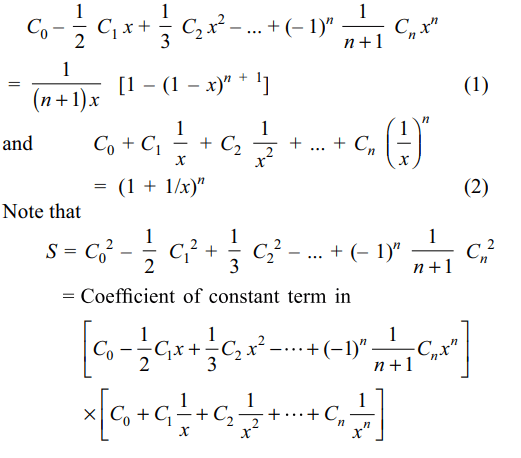

7. Sum of the coefficients of the terms of
degree m in the expansion of\[\left(1+x\right)^{n}\left(1+y\right)^{n}\left(1+z\right)^{n}\] is
a) \[\left(^{n}C_{m}\right)^{3}\]
b) \[3\left(^{n}C_{m}\right)\]
c) \[^{n}C_{3m}\]
d) \[^{3n}C_{m}\]
Explanation:
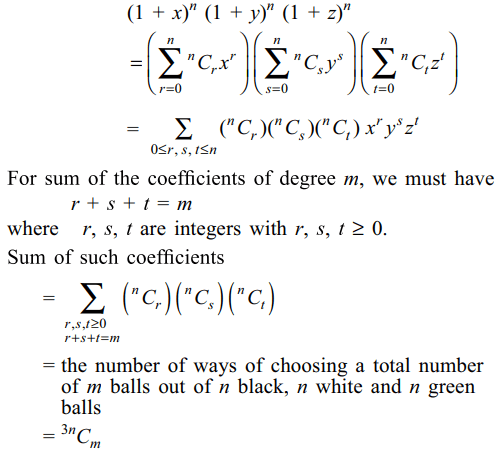
8. If A and B are coefficients of \[x^{n}\] in the
expansions of \[\left(1+x\right)^{2n}\] and \[\left(1+x\right)^{2n-1}\] respectively, then A/B is equal to
a) 1
b) 2
c) 1/2
d) 1/n
Explanation: We know that coefficient of xr in the
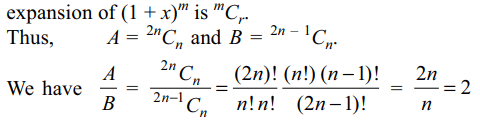
9. The coefficient of \[x^{k}\] in the expansion of
\[E=1+\left(1+x\right)+\left(1+x\right)^{2}+...+\left(1+x\right)^{n}\] is
a) \[^{n}C_{k}\]
b) \[^{n+1}C_{k}\]
c) \[^{n+1}C_{k+1}\]
d) \[^{n}C_{k+1}\]
Explanation:
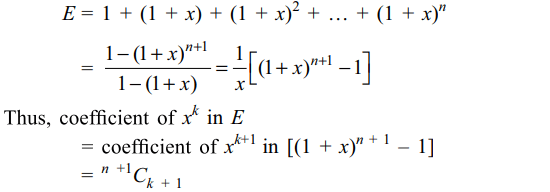
10. The number of irrational terms in the
expansion of \[\left(5^{1/6}+2^{1/8}\right)^{100}\] is
a) 96
b) 97
c) 98
d) 99
Explanation: