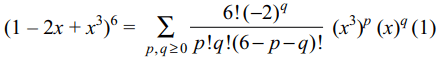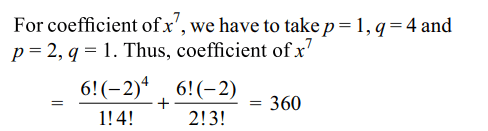1. If n > 2, then \[C_{1}\left(a-1\right)^{2}-C_{2}\left(a-2\right)^{2}+C_{3}\left(a-3\right)^{2}+....+\left(-1\right)^{n-1}C_{n}\left(a-n\right)^{2}\]
is equal to
a) na
b) \[a^{2}\]
c) \[a^{2}-2a\]
d) 0
Explanation: The given expression can be written as
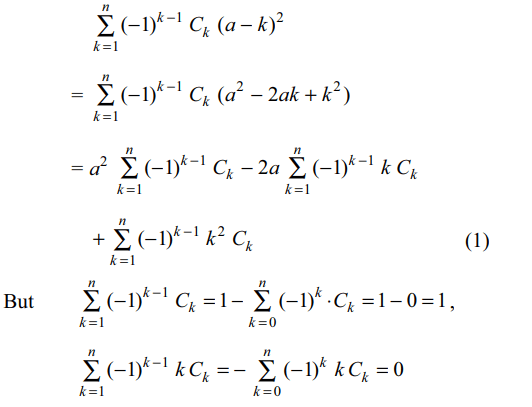
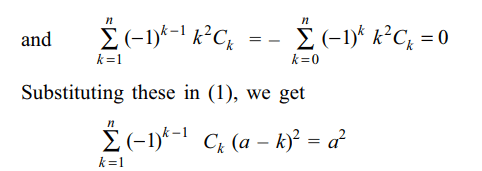
2. If \[x\epsilon R\] , and \[S=1-C_{1}\frac{1+x}{1+nx}+C_{2}\frac{1+2x}{\left(1+nx\right)^{2}}-C_{3}\frac{1+3x}{\left(1+nx\right)^{3}}\] + .... upto (n+1) terms
Then S
a) is independent of x
b) equals 1
c) equals 0
d) Both a and c
Explanation:
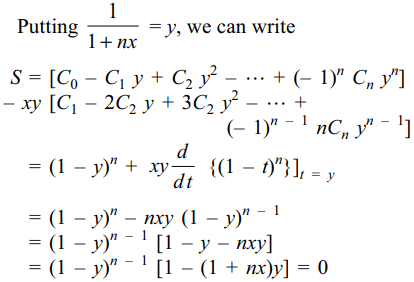
3. If \[\left(x^{2017}+x^{2018}+2\right)^{2010}=a_{0}+a_{1}x+a_{2}x^{2}+....+a_{n}x^{n}\] (1)
then value of
\[a_{0}-\frac{1}{2}a_{1}-\frac{1}{2}a_{2}+a_{3}-\frac{1}{2}a_{4}-\frac{1}{2}a_{5}+a_{6}+....\]
is
a) less than 2
b) greater than 0
c) equals 2
d) Both a and b
Explanation:

4. Let \[\left(1+\sqrt{2}\right)^{n}=x_{n}+y_{n}\sqrt{2}\]
where \[x_{n}, y_{n}\] are integers ,then
a) \[x_n^2-2y_n^2=\left(-1\right)^{n}\]
b) \[x_{n}+2y_{n}-x_{n+1}=0\]
c) \[y_{n+1}=x_{n}+y_{n}\]
d) All of the above
Explanation:
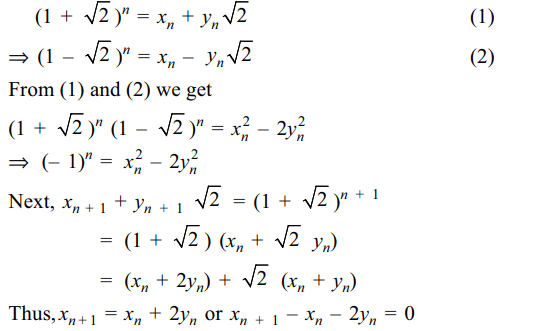
5. 11th term in the expansion of \[\left(3-\sqrt{\frac{17}{14}+3\sqrt{2}}\right)^{20}\]
is
a) an irrational number
b) a rational number
c) a positive integer
d) Both b and c
Explanation:
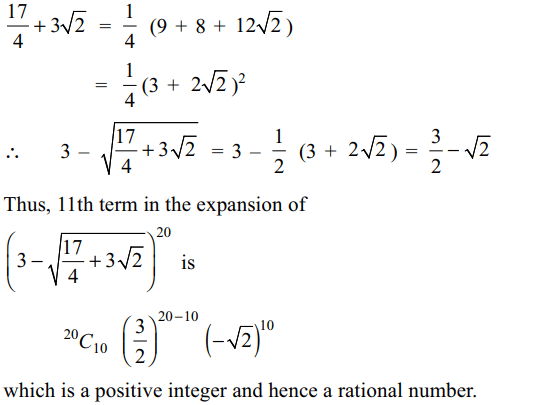
6. Let S denote the set of real numbers such
that
\[\left(x+\sqrt{x^{2}-1}\right)^{5}+\left(x-\sqrt{x^{2}-1}\right)^{5}=2\cos \left(\pi\cos^{-1}x\right)\] (1)
Then S contains
a) at least two elements
b) at most two elements
c) infinite number of elements
d) Both a and b
Explanation: LHS of (1) is defined for x2 ≥ 1
RHS of (1) is defined for x2 \[\leq\] 1
Thus, (1) is defined for x = ± 1
For x = 1, LHS = 2 and RHS = 2
For x = –1, LHS = –2 and RHS = –2
7. The real values of a, b, p, q for which \[\left(2x-1\right)^{20}-\left(ax+b\right)^{20}=\left(x^{2}+px +q\right)^{10}\]
are
a) \[2b=-a=\pm\left(2^{20}-1\right)^{1/20},p=q=1/2\]
b) \[b=-2a=\pm\left(2^{20}-1\right)^{1/20},p=q=1/4\]
c) \[2b=-a=\pm\left(2^{20}-1\right)^{1/20},4q=-p=1\]
d) none of these
Explanation: Equating coefficients of x20, we get
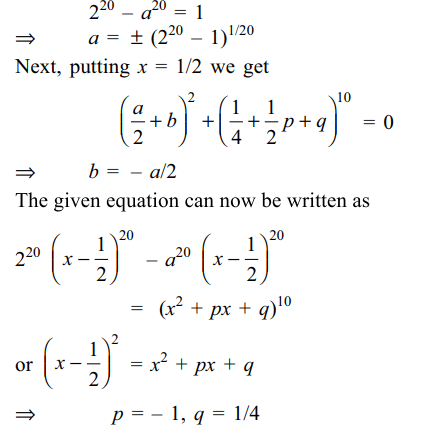
8. Sum of the series \[S=\sum_{r=0}^{n}\frac{3^{r+4}\left(^{n}C_{r}\right)}{^{r+4}C_{4}}+\sum_{r=0}^{3}\frac{^{n+4}C_{r}3^{r}}{^{n+4}C_{4}}\]
is
a) \[4^{n+4}\]
b) \[4^{n+4}\left(^{2n}C_{4}\right)\]
c) \[\frac{4^{n+4}}{^{n+4}C_{4}}\]
d) \[\frac{3^{n+4}+2^{n+4}}{^{n+4}C_{4}}\]
Explanation:
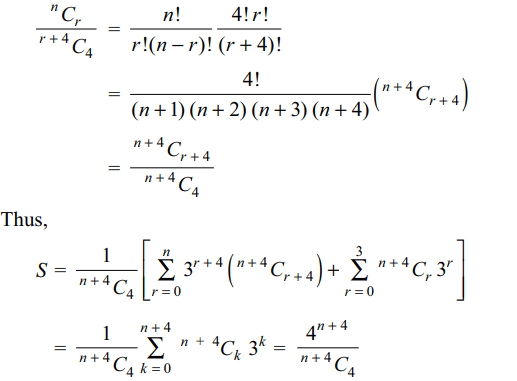
9. Let \[S=C_{1}-\left(1+\frac{1}{2}\right)C_{2}+\left(1+\frac{1}{2}+\frac{1}{3}\right)C_{3}-....+\left(-1\right)^{n-1}\left(1+\frac{1}{2}....+\frac{1}{n}\right)C_{n}\]
then
a) nS = 1
b) 1/S is an integer
c) \[1/S^{2}\] is an integer
d) All of the above
Explanation: We can write S as
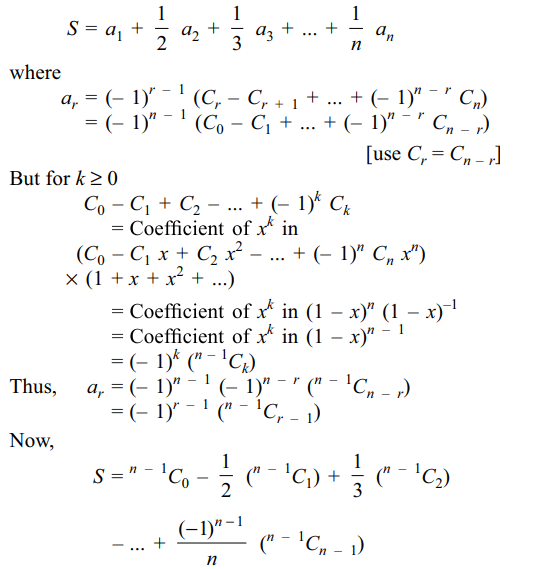
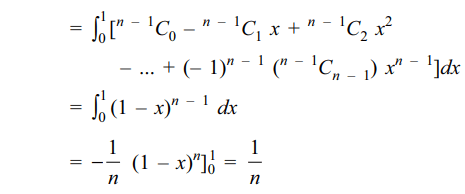
10. coeffiecient of \[x^{7}\] in the expansion of \[\left(1-2x+x^{3}\right)^{6}\] is
a) 280
b) 360
c) – 450
d) – 280
Explanation: