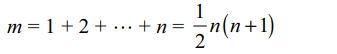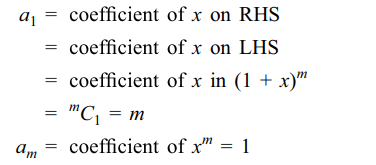1. If n is an odd natural number, then number of zeros
at the end of \[99^{n}+1\] is
a) 2
b) n
c) 2n
d) none of these
Explanation:

2. Value of \[S=\sum\sum_{0\leq r< s\leq n}^{}\left(C_{r}+C_{s}\right)^{2}\] is
a) \[2^{2n}\left(n+1\right)\left(^{2n}C_{n}\right)\]
b) \[2^{2n}+\left(n+1\right)\left(^{2n}C_{n}\right)\]
c) \[2^{2n-1}+\left(n+1\right)\left(^{2n}C_{n}\right)\]
d) none of these
Explanation:
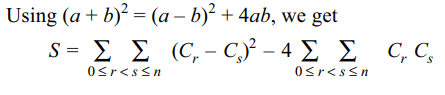
3. Value of \[S=\sum\sum_{0\leq r< s\leq n}^{}\left(r+s\right)\left(C_{r}+C_{s}\right)^{2}\]
a) \[n\left[\left(n-1\right)\left(^{2n}C_{n}\right)+2^{2n}\right]\]
b) \[n\left[\left(n+1\right)\left(^{2n}C_{n}\right)+2^{2n}\right]\]
c) \[n\left[2^{2n}-n\left(^{2n}C_{n}\right)\right]\]
d) none of these
Explanation:
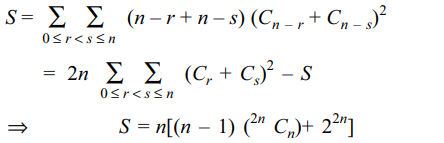
4. Value of S = \[\sum_{k=1}^{\infty}\sum_{r=0}^{k}\frac{1}{3^{k}}\left(^{k}C_{r}\right)\] is
a) 2
b) \[\frac{2}{3}\]
c) \[\frac{1}{3}\]
d) none of these
Explanation:
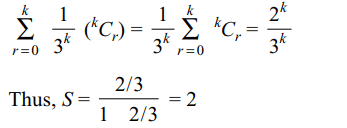
5. Value of \[S=^{n}C_{r}+3\left(^{n-1}C_{r}\right)+5\left(^{n-2}C_{r}\right)+....upto \left(n-r+1\right)\] terms is
a) \[^{n+2}C_{r+2}\]
b) \[^{n+2}C_{r+2}+^{n+1}C_{r+2}\]
c) \[^{n+2}C_{r+1}\]
d) \[^{n+2}C_{r+2}+^{n+1}C_{r}\]
Explanation:
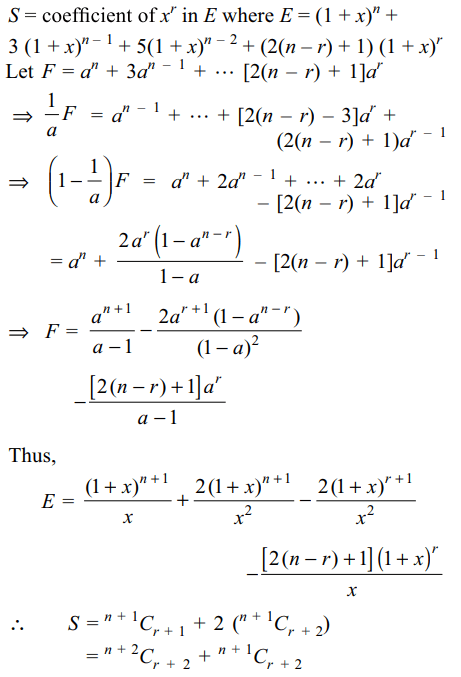
6. If n is a multiple of 3 and \[\left(1+x+x^{2}\right)^{n}=\sum_{r=0}^{2n}a_{r}x_{r}\]
and
\[\sum_{r=0}^{n}(-1)^{r}a_{r}\left(^{n}C_{r}\right)=k\left(^{n}C_{n/3}\right)\]
then value of k is
a) 0
b) 1
c) 2
d) none of these
Explanation: none of these
7. If the middle term of \[\left(1+x\right)^{2n}\] is also the largest term
then x lies in the interval
a) \[\left(1-\frac{1}{n+1},1+\frac{1}{n}\right)\]
b) \[\left(1-\frac{1}{n},1+\frac{1}{n}\right)\]
c) (0, 1)
d) (– 1/n, 1/n)
Explanation:
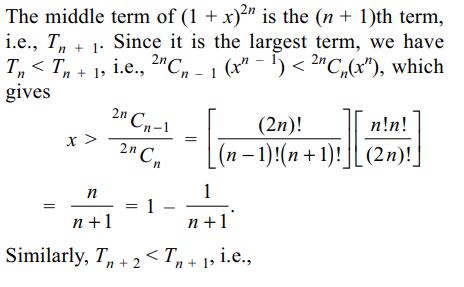
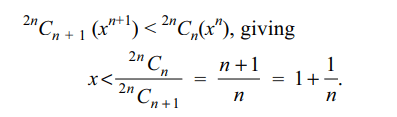
8. Sum of the series \[S=\sum_{r=0}^{n}\left(-1\right)^{r}\left(^{n}C_{r}\right)\left[\frac{2^{r}}{3^{r}}+\frac{8^{r}}{3^{2r}}+\frac{26^{r}}{3^{3r}}+...upto \infty\right]\]
is
a) \[\frac{2}{3^{n}-1}\]
b) \[\frac{1}{3^{n}+1}\]
c) \[\frac{1}{3^{n}-1}\]
d) \[\frac{2}{3^{n}+1}\]
Explanation:
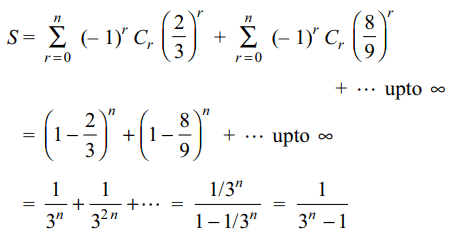
9. The ratio of the coefficients of \[x^{15}\] to the term independent
of x in the expansion of
\[\left(x^{2}+\frac{2}{x}\right)^{15}\] is
a) 1 : 8
b) 1 : 12
c) 1 : 16
d) 1 : 32
Explanation:
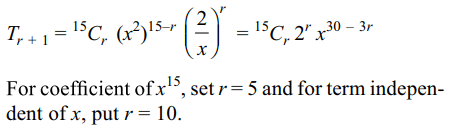
10. If \[\left(1+x\right)\left(1+x+x^{2}\right)\left(1+x+x^{2}+x^{3}\right)...\left(1+x+...+x^{n}\right)=a_{0}+a_{1}x+a_{2}x^{2}+...a_{m}x^{m}, \]
then
a) \[m=\frac{1}{2}n\left(n+1\right)\]
b) \[a_{1}=m\]
c) \[a_{m}=1\]
d) All of the above
Explanation: