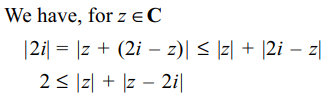1. All the solutions of \[Z^{2018}+\frac{1}{Z^{2018}}+Z^{2016}+\frac{1}{Z^{2016}}=0\]
lie on the curve
a) \[\mid Z\mid=1\]
b) \[\mid Z\mid=1/2018\]
c) \[\mid Z\mid=1/2016\]
d) \[\mid Z\mid=1/4034\]
Explanation:

2. Let \[z_{k}=a_{k}+ib_{k}\neq0,\] for \[k=1,2...,2018\] . Then value of the expression
\[E=\frac{\mid\left(\sum_{k=1}^{2018}\left(a_{k}-b_{k}\right)\right)\left(\sum_{k=1}^{2018}\left(a_{k}+b_{k}\right)\right)\mid}{\left(\sum_{k=1}^{2018}\mid z_{k} \mid\right)^{2}}\]
a) is at least 2018
b) is at least 1009
c) is always less than 2
d) is always greater than 2
Explanation:
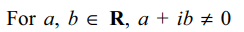
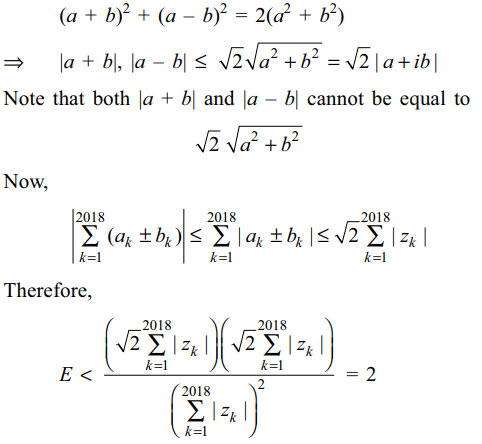
3. Let \[\omega\] be a complex number such that
\[\mid\omega \mid =\sqrt{2}.\] Let \[\alpha,\beta\] be solution of the equation
\[z^{2}+i\left(\omega+i\bar{\omega}\right)z-2i=0\]
then
a) \[\mid\alpha\mid+\mid\beta\mid=2\]
b) \[\mid\alpha-\beta\mid=2\]
c) \[\mid\alpha\mid+\mid\beta\mid=2\sqrt{2}\]
d) \[\mid\alpha-\beta\mid=2\sqrt{2}\]
Explanation:
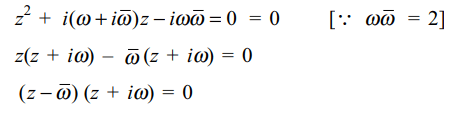
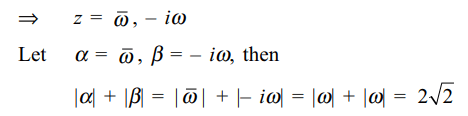
4. If a, b are distinct complex numbers
lying on the unit circle |z| = 1, then value of
\[\mid\frac{a+b}{1+ab}\mid^{2}+\mid\frac{a-b}{1-ab}\mid^{2}\]
a) cannot exceed 2
b) is at least 1
c) is at most 2
d) is at least 2
Explanation:
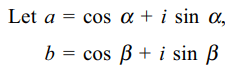
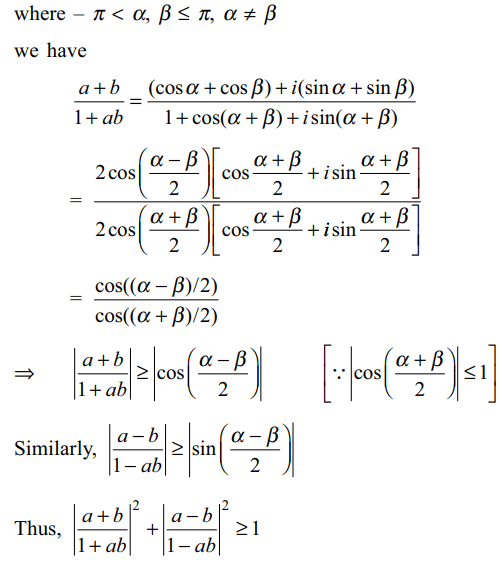
5. Let \[a_{1}=2 , a_{n+1}=\frac{a_{n}-i}{a_{n}+i}\] for \[n\geq 1 \] ,
then \[\sum_{k=1}^{3n}a_{k}\] is equal to
a) \[\frac{n}{5}(13-19i)\]
b) \[\frac{1}{5}(13-19i)\]
c) \[n(2+3i)\]
d) \[n(3-2i)\]
Explanation:
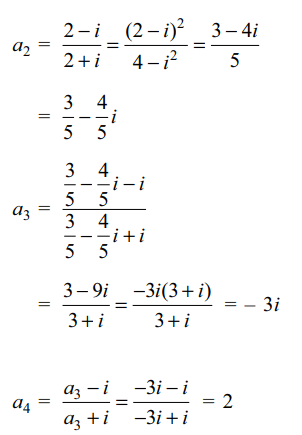
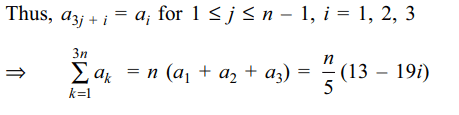
6. Let a, b, c and d be four distinct complex
numbers such that |a| = |b| = |c| = 1.
If \[z=\frac{\left(a-c\right)\left(b-d\right)}{\left(a-d\right)\left(b-c\right)}\]
is real, then
a) d is a real number
b) d = 0
c) d is a purely imaginary
d) |d| = 1
Explanation:
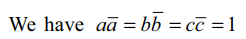
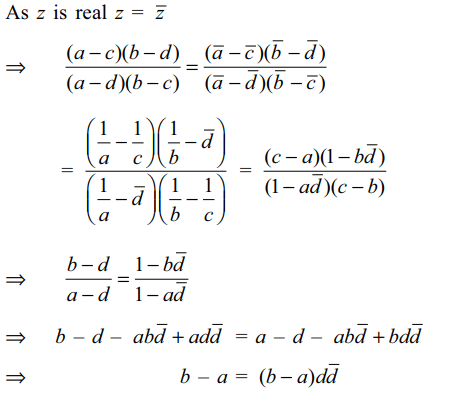
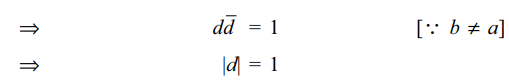
7. Let p and q be two complex numbers such
that q \[\neq\] 0. If the roots of the equation \[x^{2}+px+q^{2}=0\] have
the same absolute value, then p/q is
a) an integer
b) a rational number
c) a real number
d) a complex number
Explanation: Let x1, x2 be the roots of x2 + px + q2 = 0 and
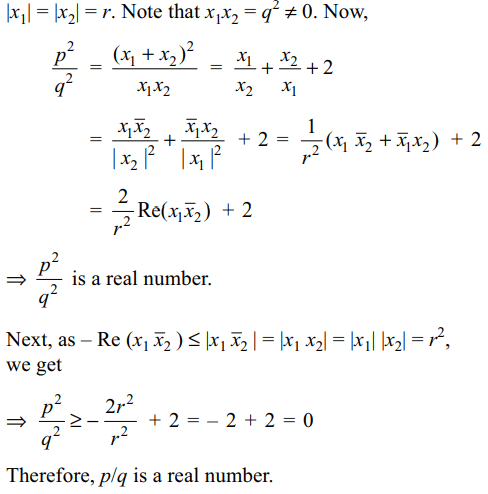
8. If \[\mid z^{3}+\frac{1}{z^{3}}\mid \leq2\] , then \[\mid z+\frac{1}{z}\mid \]
cannot exceed
a) 2
b) 1
c) \[\sqrt{2}\]
d) \[\sqrt{2}-1\]
Explanation:
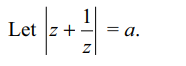
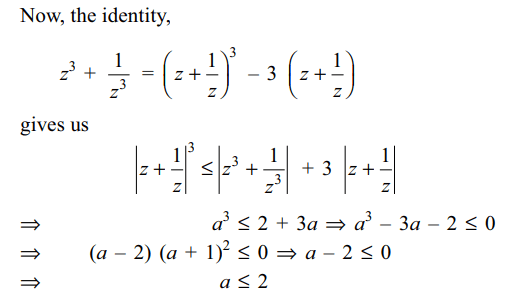
9. If \[\omega=\cos\frac{\pi}{n}+i\sin\frac{\pi}{n}\] then value of
\[1+\omega+\omega^{2}+....+\omega^{n-1}\] is
a) 1 + i
b) \[1+i\tan\left(\pi/n\right)\]
c) \[1+i\cot\left(\pi/2n\right)\]
d) 1 – i
Explanation:
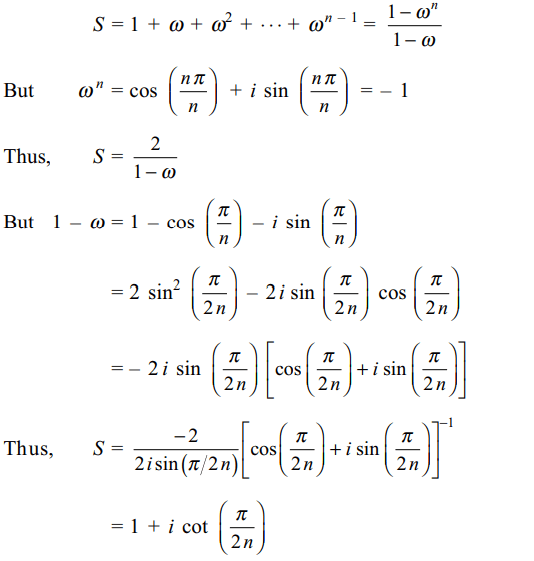
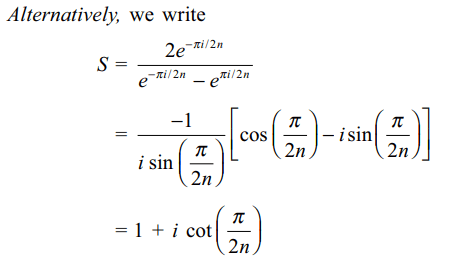
10. For any complex number z, the minimum
value of |z| + | z – 2i| is
a) 0
b) 1
c) 2
d) \[\sqrt{3}\]
Explanation: