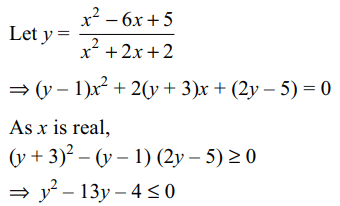1. Let \[f\left(x\right)=x^{3}+3x^{2}+6x+2009\] and
\[g\left(x\right)=\frac{1}{x-f\left(1\right)}+\frac{2}{x-f\left(2\right)}+\frac{3}{x-f\left(3\right)}\]
The number of real solutions of g(x) = 0 is
a) 0
b) 1
c) 2
d) infinite
Explanation:
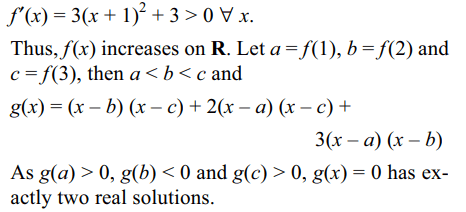
2. Let \[\alpha,\beta \epsilon R ,\beta\neq 0\] and \[\alpha+i\beta\] be a root of
\[x^{3}+qx+r=0\] where \[q, r \epsilon R\] . A cubic equation with real coefficients one of whose roots is \[\alpha\]
, is
a) \[x^{3}-qx+r=0\]
b) \[x^{3}+2qx+r=0\]
c) \[x^{3}+4qx-8r=0\]
d) none of these
Explanation:

3. Suppose a, b are complex numbers and
\[x^{3}+ax+b=0\] has a pair of complex conjugate roots,
then
a) a is real and b is imaginary
b) a is imaginary and b is real
c) both a and b are real
d) none of these
Explanation:
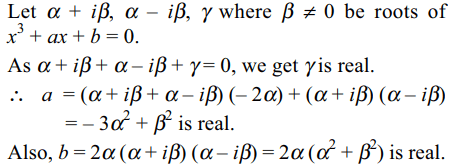
4. The number of solution of \[10^{2/x}+25^{1/x}=\left(\frac{65}{8}\right)\left(50^{1/x}\right)\]
is
a) 0
b) 1
c) 2
d) infinite
Explanation:
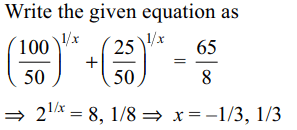
5. The equation \[\left(\frac{10}{9}\right)^{x}= - 3x^{2}+2x-\frac{9}{11}\]
has
a) no solution
b) exactly one solution
c) exactly two solutions
d) none of these
Explanation:
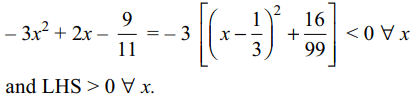
6. Let \[a,b,c \epsilon R\] and a \[\neq\] 0 be such that \[\left(a+c\right)^{2}< b^{2}\] ,
then the quadratic equation \[ax^{2}+bx+c=0\] has
a) imaginary roots
b) real roots
c) two real roots lying between (– 1, 1)
d) none of these
Explanation:
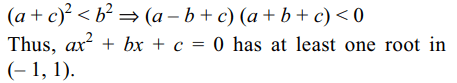
7. The number of real solution of \[4^{x+1.5}+9^{x+0.5}=\left(10\right)\left(6^{x}\right)\]
is
a) zero
b) one
c) two
d) infinite
Explanation:
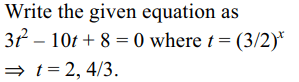
8. If roots of the equation \[x^{2}-2mx +m^{2}-1=0\] lie in
the interval (– 2, 4), then
a) – 1 < m < 3
b) 1 < m < 5
c) 1 < m < 3
d) -1 < m < 5
Explanation:
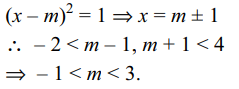
9. The number of solutions of the equation
\[\sin \left(\frac{\pi x}{2\sqrt{3}}\right)=x^{2}-2\sqrt{3}x+4\]
is
a) 1
b) 2
c) 0
d) infinite
Explanation:
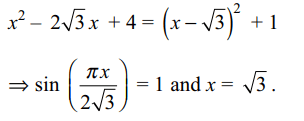
10. If x is real, then the least value of the expression
\[\frac{x^{2}-6x+5}{x^{2}+2x+2}\]
is
a) -1
b) -1/3
c) -1/2
d) none of these
Explanation: