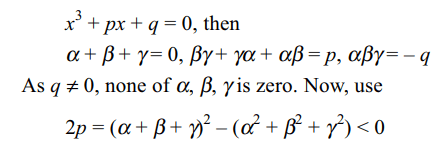PrepBharat

1. Let \[\alpha\] and \[\beta\]  be the roots of \[x^{2}-6x-2=0\]    , with \[\alpha>\beta\]  . If \[a_{n}=\alpha^{n}-\beta^{n}\]    for \[n\geq 1\] , then the value of \[\frac{a_{10}-2a_{8}}{2a_{9}}\]   is
a) 3
b) 2
c) 1
d) 4

View Answer

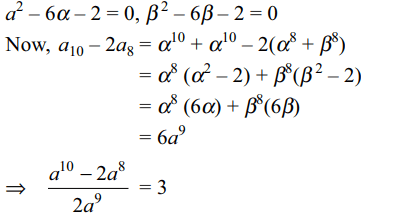
2. A value of b for which the equations
\[x^{2}+bx-1=0\]
\[x^{2}+x+b=0\]
have one root in common is
a) \[-\sqrt{2}\]
b) \[i\sqrt{5}\]
c) \[i\sqrt{3}\]
d) \[\sqrt{2}\]

View Answer

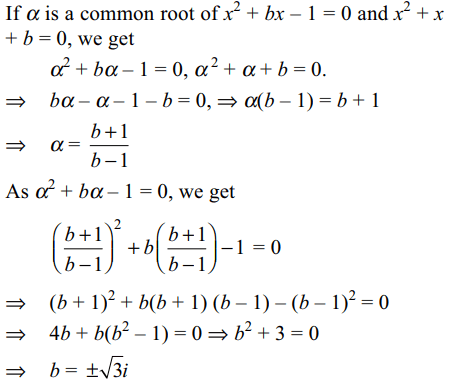
3. If \[x \epsilon R\] , the number of solutions of \[\sqrt{2x+1}-\sqrt{2x-1}=1\]     is
a) 0
b) 1
c) 4
d) infinite

View Answer

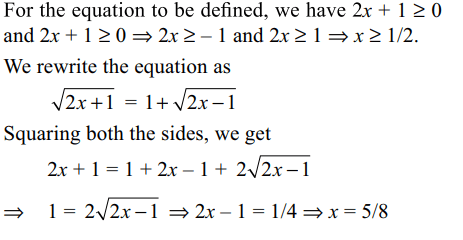
4. If l, m, n are real, \[l+m\neq0\]   , then the roots of the equation \[\left(l+m\right)x^{2}-3\left(l-m\right)x-2\left(l+m\right)=0\]
a) real and unequal
b) complex
c) real and equal
d) purely imaginary

View Answer

5. If the equation \[\sqrt{x+1}-\sqrt{x}=a\]    has a solution, then
a) 0 < a < 1
b) a > 1
c) \[0 < a \leq 1\]
d) \[ a \leq 1\]

View Answer

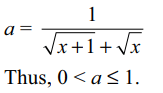
6. Let \[\alpha\] , \[\beta\] be the roots of the equation \[x^{2}-ax+b=0\]     and \[A_{n}=\alpha^{n}+\beta^{n}\]    . Then \[A_{n+1}-aA_{n}+bA_{n-1}\]     is equal to
a) -a
b) b
c) a-b
d) 0

View Answer

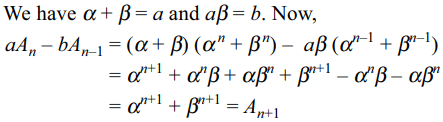
7. If \[\alpha,\beta,\gamma\]  are such that \[\alpha+\beta+\gamma=2,\alpha^{2}+\beta^{2}+\gamma^{2}=6,\alpha^{3}+\beta^{3}+\gamma^{3}=8\]
then \[\alpha^{4}+\beta^{4}+\gamma^{4}\]    is
a) 5
b) 18
c) 12
d) 36

View Answer

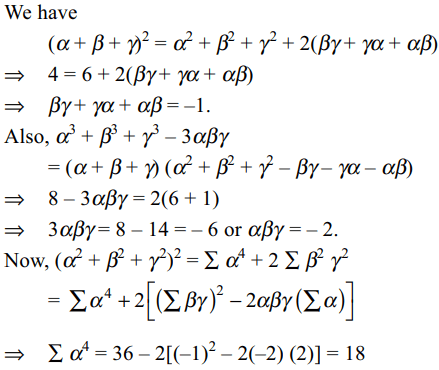
8. In a triangle PQR, \[\angle\] R = \[\pi\] /4. If tan (P/3) and tan (Q/3) are the roots of the equation ax² + bx + c = 0, then
a) a + b = c
b) b + c = 0
c) a + c = b
d) b = c

View Answer

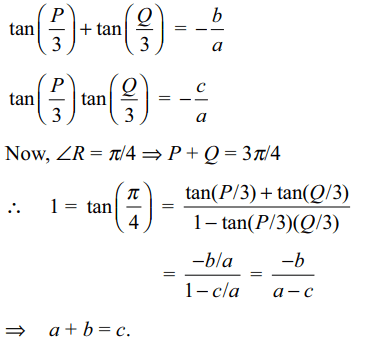
9. The product of the roots of \[\sqrt[3]{8+x}+\sqrt[3]{8-x}=1\]     is
a) -21
b) -189
c) -9
d) -5

View Answer

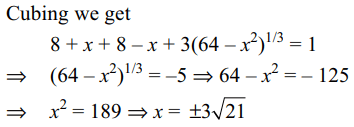
10. If all the roots of \[x^{3}+px+q=0\]    p, q \[\epsilon\] R , \[q\neq 0\]  are real, then
a) p < 0
b) p = 0
c) p > 0
d) p > q

View Answer