1. If tan A and tan B are the roots of
the quadratic equation \[x^{2}-px+q=0\] , then value of
\[\sin^{2}\left(A+B\right)\] is
a) \[\frac{p^{2}}{p^{2}+q^{2}}\]
b) \[\frac{p^{2}}{\left(q+p\right)^{2}}\]
c) 1 - \[\frac{p}{\left(1-q\right)^{2}}\]
d) \[\frac{p^{2}}{\left(1-q\right)^{2}+p^{2}}\]
Explanation: We have tan A + tan B = p, and tan A tan B = q
2. The real value of a for which the sum of
the squares of the roots of the equation
\[x^{2}-\left(a-2\right)x-a-1=0\] assume the least value is
a) 0
b) 1
b) 2
c) 3
Explanation: Discriminant of the equation is

3. If p and q are distinct primes and \[x^{2}-px+q=0\] has distinct positive integral roots, then p + q equals
a) 5
b) 7
c) 19
d) 40
Explanation: Let \[\alpha\] and \[\beta\] be two roots of x2– px + q = 0 and
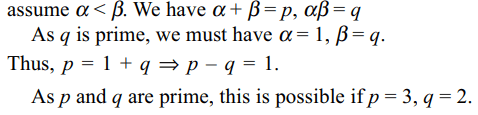
4. The real values of a for which the
quadratic equation \[3x^{2}+2\left(a^{2}+1\right)x+\left(a^{2}-3a+2\right)=0\]
possesses roots of opposite signs lie in
a) \[\left(-\infty,1\right)\]
b) \[\left(-\infty,0\right)\]
c) \[\left(1,2\right)\]
d) \[\left(\frac{3}{2},2\right)\]
Explanation: The quadratic equation \[3x^{2}+2\left(a^{2}+1\right)x+\left(a^{2}-3a+2=0\right)\] will have two roots of opposite signs if it has real roots and the product of the roots is negative, that is, if

5. If \[a,b,c \epsilon R\] and a + b + c = 0, then the
quadratic equation \[3ax^{2}+2bx+c=0\] has
a) at least one root in [0, 1]
b) at least one root in [1, 2]
c) at least one root in [3/2, 2]
d) none of these
Explanation: Let f(x) = ax3 + bx2 + cx. Note that f is continuous and derivable on R. Also f(0) = 0 and f(1) = a + b + c = 0. By the Rolle’s theorem, there exists at least one \[\alpha\] \[\epsilon\] (0, 1) such that

6. Let \[f\left(x\right)=ax^{2}+bx+c,a,b,c\epsilon R\] and
\[a\neq 0\] . Suppose f (x) > 0 for all \[x \epsilon R\] .
Let\[g\left(x\right)=f\left(x\right)+f'\left(x\right)+f''\left(x\right)\] . Then
a) \[g\left(x\right)>0 \forall\] \[x \epsilon R\]
b) \[g\left(x\right)< 0 \forall\] \[x \epsilon R\]
c) \[g\left(x\right)=0 \forall\] \[x \epsilon R\]
d) g(x) = 0 has real roots
Explanation:
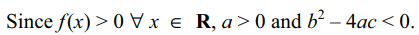

7. If b < 0, then the roots \[x_{1}\] and \[x_{2}\] of the
equation \[2x^{2}+6x+b=0\] , satisfy the condition \[\left(x_{1}/x_{2}\right)+\left(x_{2}/x_{1}\right)< k\] where k is equal to.
a) -3
b) -5
c) -6
d) -2
Explanation: The discriminant of the quadratic equation
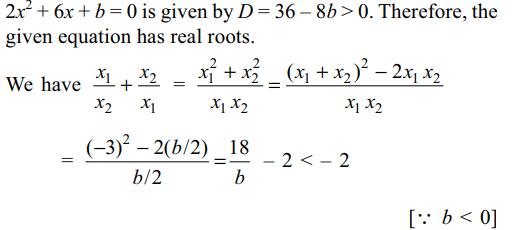
8. If \[ax^{2}+bx+c,a,b,c \epsilon R\] has no real
zeros, and if c < 0, then,
a) a < 0
b) a+b+c>0
c) a > 0
d) none of these
Explanation: Let f (x) = ax2 + bx + c. Since f (x) has no real zeros, either f (x) > 0 or f (x) < 0 for all x \[\epsilon\] R. Since f (0) = c < 0, we get f (x) < 0 \[\forall\] x \[\epsilon\] R. Therefore, a < 0 as the parabola y = f (x) must open downwards.
9. If x is real, then the maximum value of
\[y=2 \left(a-x \right)\left(x+\sqrt{x^{2}+b^{2}}\right)\]
is
a) \[a^{2}+b^{2}\]
b) \[a^{2}\]
c) \[\sqrt{a^{2}+b^{2}}\]
d) \[a\sqrt{a^{2}+b^{2}}\]
Explanation:
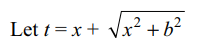
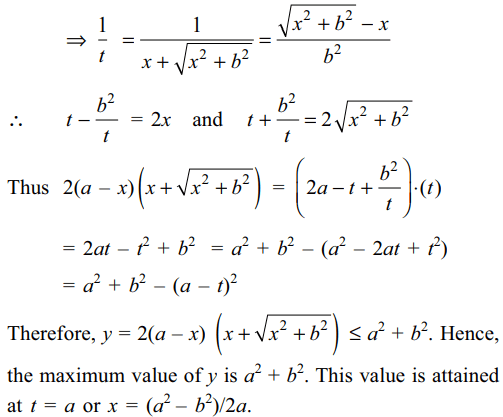
10. If both the roots of the equation
\[x^{2}-6ax+2-2a+9a^{2}=0\] exceed 3, then
a) a < 1
b) a > 11/9
c) a > 3/2
d) a < 5/2
Explanation: