1. Let \[f\left(x\right) = ax^{2}+bx+c,a,b,c \epsilon R\] . If f (x)
takes real values for real values of x and non-real values for
non-real values of x, then.
a) a=0
b) b=0
c) c=0
d) nothing can be said about a, b, c.
Explanation: Suppose a \[\neq\] 0. We rewrite f (x) as follows:
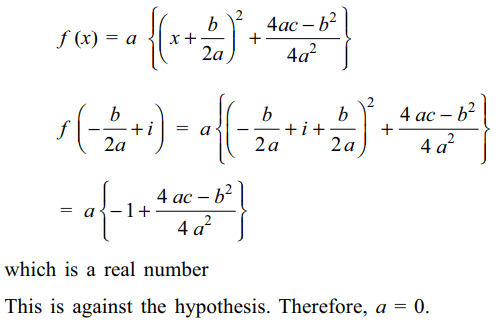
2. The condition that the equation
\[\frac{1}{x}+\frac{1}{x+b}=\frac{1}{m}+\frac{1}{m+b}\]
has real roots that are equal in magnitude but opposite in
sign is
a) \[b^{2}=m^{2}\]
b) \[b^{2}=2m^{2}\]
c) \[2b^{2}=m^{2}\]
d) none of these
Explanation: Clearly x = m is a root of the equation. Therefore, the other root must be – m. That is,
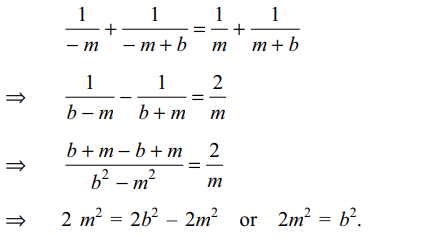
3. If x is real, and \[k=\frac{x^{2}-x+1}{x^{2}+x+1}\]
then
a) \[1/3\leq k\leq 3\]
b) \[k\geq 5\]
c) \[k\leq 0\]
d) \[2/3\leq k\leq 1\]
Explanation:

4. Let a > 0, b > 0 and c > 0. Then both the
roots of the equation \[ax^{2}+bx+c=0\]
a) are real and negative
b) have negative real parts
c) are rational numbers
d) none of these
Explanation:
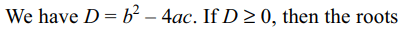
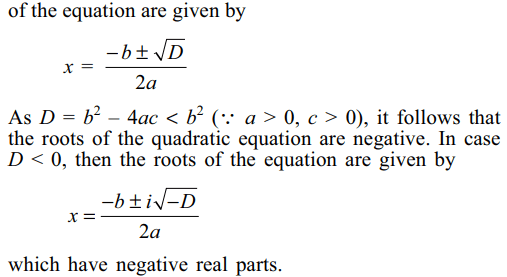
5. Let a, b, c be non-zero real numbers such
that
\[\int_{0}^{1} \left(e^{-x}+e^{x}\right)\left(ax^{2}+bx+c\right)dx=\int_{0}^{2} \left(e^{-x}+e^{x}\right)\left(ax^{2}+bx+c\right)dx\]
Then the quadratic equation ax2 + bx + c = 0 has
a) no root in (0, 1)
b) at least one root in (1, 2)
c) a double root in (0, 1)
d) none of these
Explanation:

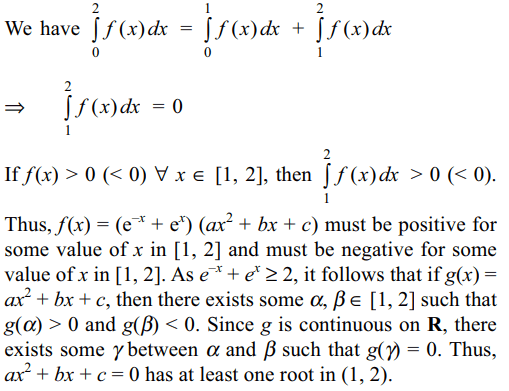
6.The equation\[\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\]
has
a) no solution
b) only one solution
c) only two solution
d) more than two solutions
Explanation:
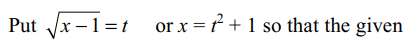
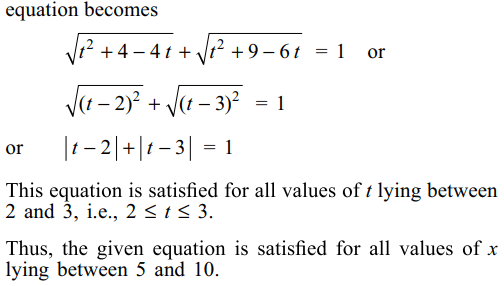
7. The equation \[3^{x-1}+5^{x-1}=34\] has
a) no solution
b) one solution
c) two solution
d) more than two solutions
Explanation: It is quite clear that x = 3 satisfies the given
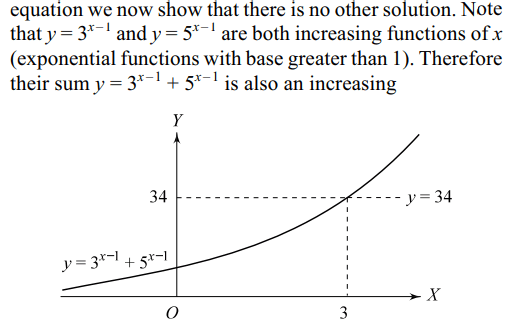
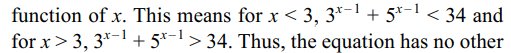
solution.
8. If the harmonic mean between roots of
\[\left(5+\sqrt{2}\right)x^{2}-bx+8+2\sqrt{5}=0\] (1)
is 4 then b equals
a) 2
b) \[4-\sqrt{5}\]
c) 3
d) \[4+\sqrt{5}\]
Explanation: Let \[\alpha\] , \[\beta\] be the roots of (1), then

9. If \[a \leq0 \] , then number of real roots of
\[x^{2}+2a\mid x-a\mid +3a^{2}=0\] (1)
is
a) 0
b) 1
c) 2
d) infinite
Explanation: Put x – a = t and rewrite (1) as

10. Let \[\left( a_{1},a_{2},a_{3},a_{4},a_{5}\right)\] denote a
rearrangement of (3, – 5, 7, 4, – 9), then the equation
\[ a_{1}x^{4}+a_{2}x^{3}+a_{3}x^{2}+a_{4}x+a_{5}=0\]
has
a) at least two real roots
b) all four real roots
c) only imaginary roots
d) none of these
Explanation: x = 1 is always a root of the equation