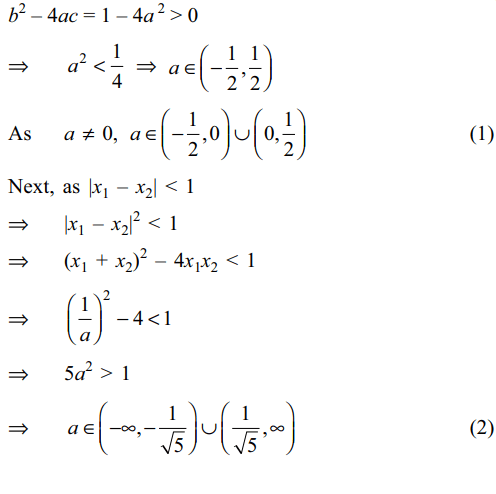1. If three distinct real number a, b and c
satisfy \[a^{2}\left(a+p\right)=b^{2}\left(b+p\right)=c^{2}\left(c+p\right)\]
where \[p \epsilon R\] , then value of bc + ca + ab is
a) -p
b) p
c) 0
d) \[p^{2}/2\]
Explanation: If value of each relation is k, then a, b, c are roots of x3 + px2 – k = 0.
2. The number of integral roots of the
equation \[x^{4}+\sqrt{x^{4}+20}=22\]
is
a) 0
b) 2
c) 4
d) 8
Explanation: Put x4 = y and write
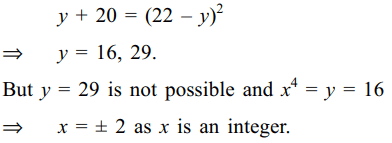
3. Let S denote the set of all values of the
parameter a for which \[x+\sqrt{x^{2}+a}=a\]
has no solution, then S equals
a) (– 1, 1)
b) \[\left(-\infty ,-1\right)\]
c) \[\left( -1,\infty\right)\]
d) \[\left( 0,\infty\right)\]
Explanation:
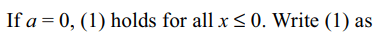
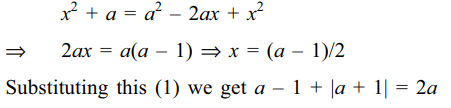
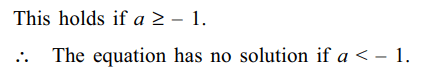
4. The number of roots of the equation \[\frac{1}{x}+\frac{1}{\sqrt{1-x^{2}}}=\frac{35}{12}\]
is
a) 0
b) 1
c) 2
d) 3
Explanation:
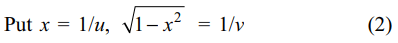
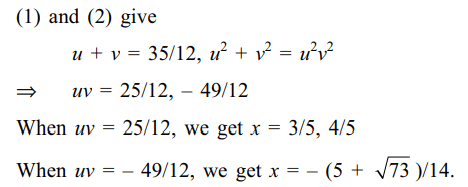
5. Let S denote the set of all real values of a
for which the roots of the equation \[x^{2}-2ax+a^{2}-1=0\]
lie between 5 and 10, then S equals
a) (– 1, 2)
b) (2, 9)
c) (4, 9)
d) (6, 9)
Explanation:
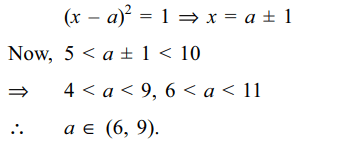
6. Let S denote the set of all values of a for
which the roots of the equation
\[\left(1+a\right)x^{2}-3ax+4a=0\] (1)
exceed 1, then S equals
a) [– 16/7, 0)
b) (– 16/7, – 1)
c) (– 1, 2)
d) (– 1, 3)
Explanation: Clearly a \[\neq\] 0, – 1. Both the roots of (1) will exceed 1 if and only if
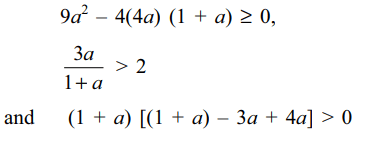
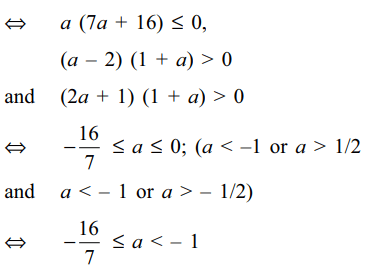
7. Let S denote the set of all values of S for
which the equations
\[2x^{2}-2\left(2a+1\right)x+a\left(a+1\right)=0\]
has one root less than a and other root greater than a, then
S equals
a) (0, 1)
b) (– 1, 0)
c) (0, 1/2)
d) none of these
Explanation:


8. Let a, b, p, q \[\epsilon\] Q and suppose that
\[f \left(x\right) = x^{2}+ax+b=0\] and \[g \left(x\right) = x^{3}+px+q=0\]
have a common irrational root, then
a) \[f \left(x\right)\] divides \[g \left(x\right)\]
b) \[g \left(x\right) \equiv xf \left(x\right)\]
c) \[g \left(x\right) \equiv \left(x-b-q\right)f\left(x\right)\]
d) None of the above
Explanation: Let \[\alpha\] \[\epsilon\] R – Q be a common root of f(x) =
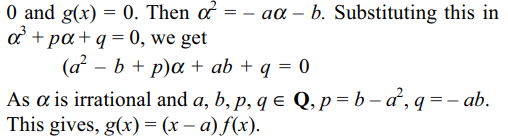
9. The number of irrational solutions of the
equation \[\sqrt{x^{2}+\sqrt{x^{2}+11}}+\sqrt{x^{2}-\sqrt{x^{2}+11}}=4\] (1)
is
a) 0
b) 2
c) 4
d) 11
Explanation:

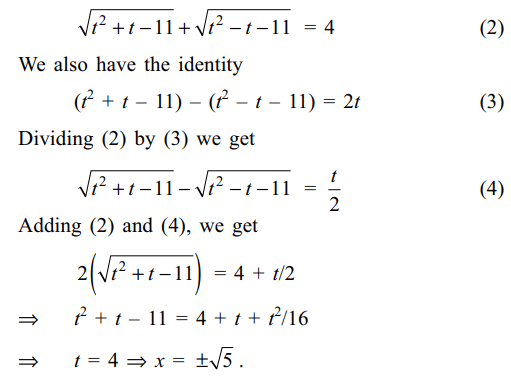
10. Let S be the set of all non-zero real
numbers a such that the quadratic equation \[ax^{2}-x+a=0\] has two distinct real roots \[x_{1}\] and\[x_{2}\] satisfying the
inequality \[\mid x_{1}-x_{1}\mid < 1\] . Which of the following intervals
is(are) a subset(s) of S?
a) \[\left(-\frac{1}{2},-\frac{1}{\sqrt{5}}\right)\]
b) \[\left(-\frac{1}{\sqrt{5}},0\right)\]
c) \[\left(\frac{1}{\sqrt{5}},\frac{1}{\sqrt{2}}\right)\]
d) Both a and c
Explanation: As ax2 – x + a = 0 has two distinct real roots