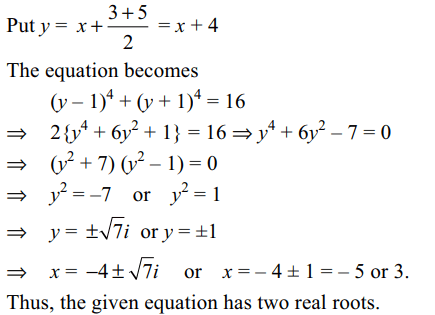1. Let a, b, c, p, q
real numbers and x, y, z be three numbers satisfying the
system of equations
\[\frac{x}{a}+\frac{y}{a-p}+\frac{z}{a-q}=1\]
\[\frac{x}{b}+\frac{y}{b-p}+\frac{z}{b-q}=1\]
\[\frac{x}{c}+\frac{y}{c-p}+\frac{z}{c-q}=1\]
then
a) x + y + z = a + b + c – p – q
b) \[x=\frac{abc}{pq}\]
c) \[y=\frac{\left(a-p\right)\left(b-p\right)\left(c-p\right)}{p\left(p-q\right)}\]
d) All of the above
Explanation: Note that a, b, c are roots of
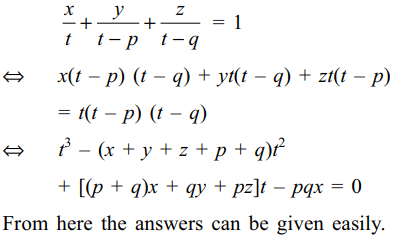
2. Let \[\alpha\] be a repeated root of
\[p\left(x\right)=x^{3}+3ax^{2}+3bx+c=0\] , then
a) \[\alpha\] is a root of \[p\left(x\right)=x^{2}+2ax+b=0\]
b) \[\alpha=\frac{c-ab }{2\left(a^{2}-b\right)}\]
c) \[\alpha\] is a root of \[ax^{2}+2bx+c=0\]
d) All of the above
Explanation:
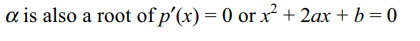

3. Let \[\alpha,\beta,\gamma\] be roots of
\[x^{3}-px^{2}+qx-r=0\] , then
a) equation whose \[\alpha^{2}-\beta\gamma, \beta^{2}-\gamma\alpha,\gamma^{2}-\alpha\beta \] is \[x^{3}+\left(3q-p^{2}\right)x^{2}+q\left(3q-p^{2}\right)x+q^{3}-p^{3}r=0\]
b) a permutation of \[\alpha,\beta,\gamma\] is in G.P. if \[q^{3}=p^{3} r\]
c) Square of one of the roots will be additive
inverse of the product of the other two if\[q^{3}=p^{3} r\]
d) Both a and b
Explanation:
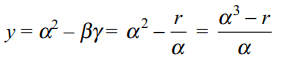
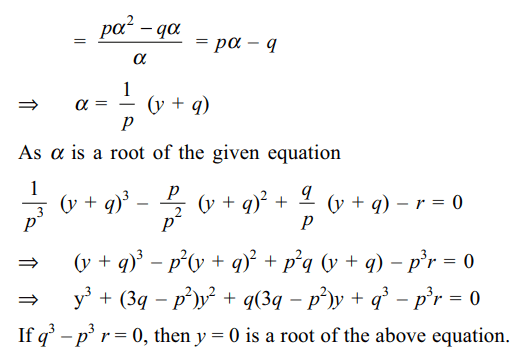
4. Let \[\alpha,\beta,\gamma\] be roots of \[x^{3}+px+q=0\] , then
a) an equation whose roots are \[\alpha^{3},\beta^{3},\gamma^{3}\] is \[x^{3}+3qx^{2}+\left(3q^{2}+p^{3}\right)y+q^{3}=0\]
b) \[\alpha^{3}+\beta^{3}+\gamma^{3}=3\alpha\beta\gamma\]
c) an equation whose roots are \[\beta^{3}+\gamma^{3},\gamma^{3}+\alpha^{3},\alpha^{3}+\beta^{3}\] is \[x^{3}+6qx^{2}+\left(p^{3}+12q^{2}\right)x+3p^{3}q+8q^{3}=0\]
d) All of the above
Explanation:
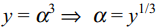
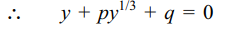
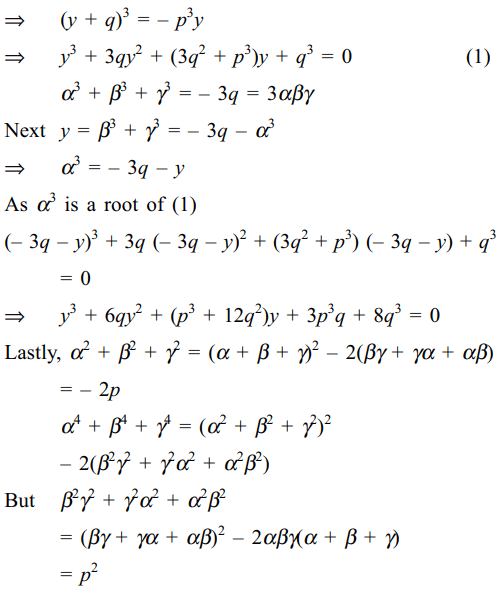
5. If the equations \[x^{2}+bx+c=0\] and
\[bx^{2}+cx+1=0\] have a common root then
a) b + c + 1 = 0
b) \[b^{2}+c^{2}+1=bc\]
c) \[\left(b-c\right)^{2}+\left(b-1\right)^{2}+\left(c-1\right)^{2}=0\]
d) Both a and c
Explanation: If \[\alpha\] is a common root of the two equations,
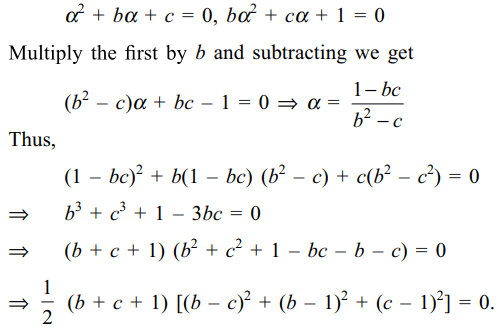
6. Let \[\alpha\] and \[\beta\] be two distinct real numbers
and p(x) be a quadratic polynomial such that \[p\left(\alpha\right)=\alpha\] and \[p\left(\beta\right)=\beta\] then
a) p(p(x)) – x = 0 has at least two real roots.
b) \[\alpha\] and \[\beta\] are roots of p(p(x)) – x = 0
c) p(p(x)) = x for each \[x \epsilon R\]
d) Both a and b
Explanation: Use p(p( \[\alpha\] )) = p( \[\alpha\] ) = \[\alpha\] and p(p( \[\beta\] )) = p( \[\beta\] ) = \[\beta\]
7. Suppose \[m \epsilon R\] . The quadratic equation
\[x^{2}-\left(m-3\right)x+m=0\] (1)
has
a) real distinct roots if and only if m \[\epsilon \left(-\infty,1\right)\cup\left(9,\infty\right)\]
b) both positive roots if and only if m \[\epsilon\] [9, \[\infty\] )
c) both negative roots if and only if m \[\epsilon\] (0,1]
d) All of the above
Explanation: (1) will have real and distinct roots
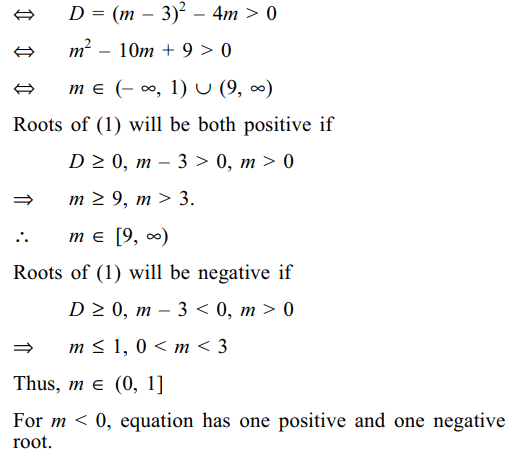
8. Let \[\alpha , \beta\] be the roots of
\[ax^{2}+2bx+c=0\] and \[\gamma ,\delta\] be the roots of \[px^{2}+2qx+r=0\] .
If \[\alpha,\beta,\gamma,\delta\] are in
a) A.P. then \[\frac{b^{2}-ac}{a^{2}}=\frac{q^{2}-pr }{p^{2}}\]
b) G.P. then \[\frac{b^{2}}{ac}=\frac{q^{2}}{pr}\]
c) H.P. then \[\frac{b^{2}-ac}{c^{2}}=\frac{q^{2}-pr }{r^{2}}\]
d) All of the above
Explanation:

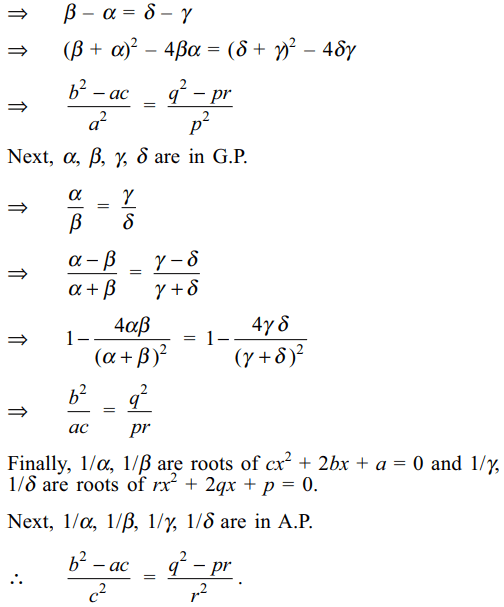
9. If \[a\left(p+q\right)^{2}+2bpq+c=0\] and
\[a\left(p+r\right)^{2}+2bpr +c=0\] , then
a) \[q+r=\frac{2\left(a+b\right)p}{a}\]
b) \[qr=p^{2}+\frac{c}{a}\]
c) \[\mid q-r\mid=\frac{2}{\mid a\mid}\sqrt{\left(2a+b\right)bp^{2}-ac}\]
d) All of the above
Explanation: q and r are roots of
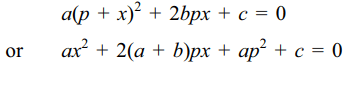
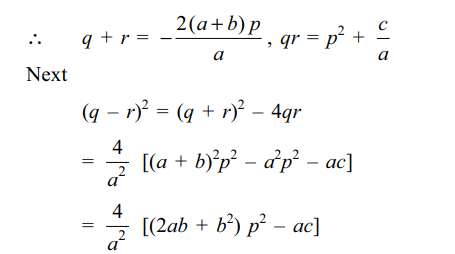
10. The number or real roots of
\[\left(x+3\right)^{4}+\left(x+5\right)^{4}=16\]
is
a) 0
b) 2
c) 3
d) 4
Explanation: