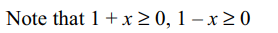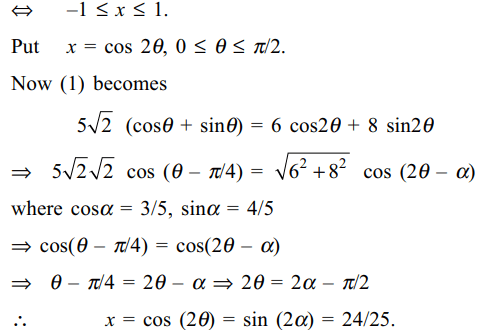1. If a > 0 and z|z| + az + 2a = 0 then z must be
a) purely imaginary
b) a positive real number
c) a negative real number
d) 0
Explanation:
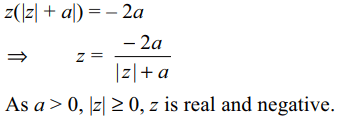
2.If \[\frac{3}{2+cos\theta+i\sin\theta}=a+ib\] , then \[\left(a-2\right)^{2}+b^{2}\]
equals
a) 0
b) 1
c) -1
d) 2
Explanation:
3. If \[z=4+i\sqrt{7}\] , then value of \[z^{3}-4z^{2}-9z+91\] equals
a) 0
b) 1
c) -1
d) 2
Explanation:
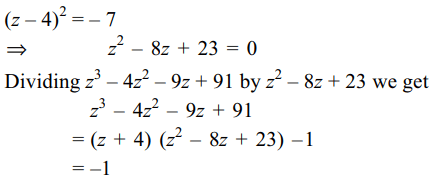
4. The number of complex number satisfying the equation |z| = 2 and |z| = |z – 1| is
a) 0
b) 1
c) 2
d) infinite
Explanation:
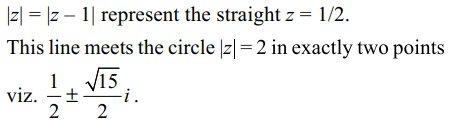
5. If \[z=\frac{mz_{1}+z_{2}}{m+1}\] , then distance of point z from the
line joining \[z_{1}+1\] and \[z_{2}+1\] is
a) 0
b) 1
c) \[\frac{2m}{m+1}\]
d) \[\frac{m}{m+1}\]
Explanation:
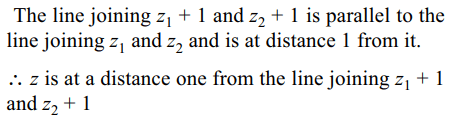
6. If \[z_{1},z_{2},z_{3}\] are three complex number such that then \[4z_{1}-7z_{2}+3z_{3}=0\] , then z1, z2, z3 are
a) vertices of a scalane triangle
b) vertices of a right triangle
c) points on a circle
d) collinear points
Explanation:
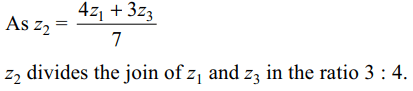
7. if a complex number z has modulus 1 and argument \[\pi/3\] , then \[z^{2}+z\]
a) is purely imaginary
b) has modulus \[\sqrt{3}\]
c) lies on the imaginary axis
d) All of the Above
Explanation:
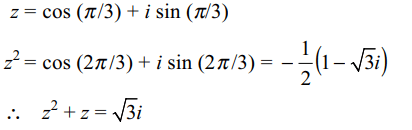
8. If \[z_{1}=a+ib\] and \[z_{2}=c+id\]
numbers such that \[\mid z_{1}\mid =\mid z_{2}\mid=1\] and Re \[\left(z_{1}\bar{z}_{2}\right)=0\] , then the pair of complex numbers, \[w_{1}=a+ic\] and \[w_{2}=b+id\] satisfy
a) \[\mid w_{1}\mid=1\]
b) \[\mid w_{2}\mid=1\]
c) \[\mid w_{1}\bar{w}_{2}\mid=1\]
d) All of the Above
Explanation:
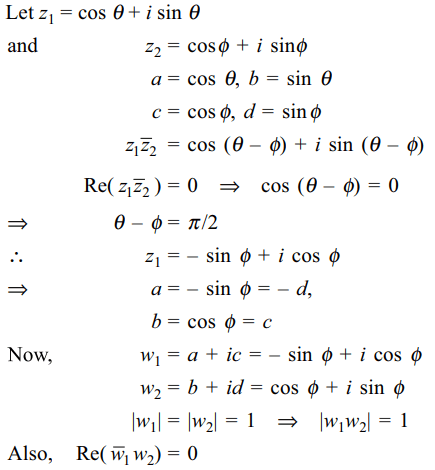
9. If \[2\cos\theta=x+\frac{1}{x}\] and \[2\cos\phi=y+\frac{1}{y}\] , then
a) \[x^{n}+\frac{1}{x^{n}}=2\cos \left(n\theta\right)\]
b) \[\frac{x}{y}+\frac{y}{x}=2\cos \left(\theta-\phi\right)\]
c) \[xy+\frac{1}{xy}=2\cos \left(\theta+\phi\right)\]
d) All of the Above
Explanation:

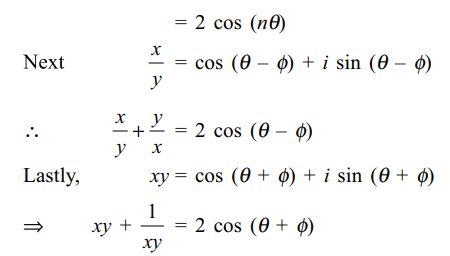
10. Number of real solutions of the equation \[5\left(\sqrt{1+x}+\sqrt{1-x}\right)=6x+8\sqrt{1-x^{2}}\]
is
a) 1
b) 2
c) 3
d) infinite
Explanation: