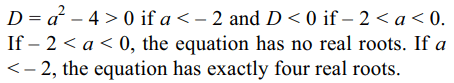1. The real values of a for which \[\frac{x^{2}-ax-2}{x^{2}-3x+4}>-1\]
for each \[x \epsilon R\] , is
a) (– 1, 2)
b) (0, 7)
c) (-7, 1)
d) (2, 7)
Explanation:

2. If \[a,b,c \epsilon R\] are distinct, then the condition(s) on
a, b, c for which the equation
\[\frac{1}{x-a}+\frac{1}{x-b}+\frac{1}{x-c}+\frac{1}{x-b-c+a}=0\]
has real roots is
a) \[a+b+c\neq 0,a\neq0\]
b) \[a-b-c\neq 0,a\neq0\]
c) 2a = b + c
d) none of these
Explanation:

3. If \[f\left(x\right)=ax^{2}+bx+c,f\left(-1\right)< 1,f\left(1\right)>-1\]
and \[f\left(-3\right)< -4\]
then
a) a = 0
b) a < 0
c) a > 0
d) sign of a cannot be determined
Explanation:

4. The set of all values of k for which the equation
\[x^{2}+2 \left(k-1\right)x+\left(k-5\right)=0\] has
at least one non-negative root is
a) \[\left[1,\infty\right)\]
b) [-1,1]
c) \[(-\infty,-5\] ]
d) \[\left[5,\infty\right)\]
Explanation:
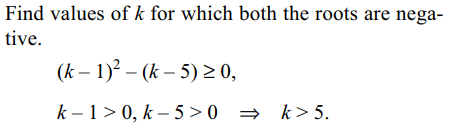
5.If \[3\pi/4<\alpha<\pi\] , then the set of values of \[\alpha\] for which
\[\left(\sin\alpha\right)x^{2}+\left(2\cos\alpha\right)x+\frac{1}{2}\left(\sin\alpha+\cos\alpha\right)\]
is square of a linear polynomial is
a) \[\left\{\frac{5\pi}{6},\frac{11\pi}{12}\right\}\]
b) \[\left\{\frac{11\pi}{12}\right\}\]
c) \[\left\{\frac{5\pi}{6}\right\}\]
d) \[\phi\]
Explanation:
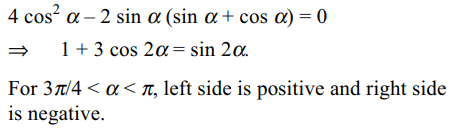
6. If \[0\leq\phi\leq3\pi\] , then the set of all values of \[\phi\] for which
sum of the squares of the roots of the equation
\[x^{2}+\left(\sin \phi -1\right)x-\frac{1}{2}\cos^{2}\phi=0\]
is greatest is
a) \[\left\{\pi,\frac{3\pi}{2},2\pi,3\pi\right\}\]
b) \[\left\{\pi,3\pi\right\}\]
c) \[\left\{2\pi,\frac{5\pi}{4}\right\}\]
d) \[\left\{\frac{3\pi}{2}\right\}\]
Explanation:
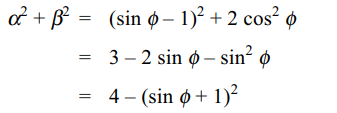
7. The set of values of b for which
\[2\log_{1/36}\left(bx+28\right)=-\log_{6}\left(12-4x-x^{2}\right)\]
has exactly one solution is
a) \[\left(-\infty,-14\right)\cup\] [14/3, \[\infty)\]
b) [14/9, \[\infty)\]
c) \[(-\infty\] ,-14] \[\cup\left\{4\right\}\cup\] [14/3,\[\infty\] ]
d) \[\left\{4\right\}\]
Explanation:
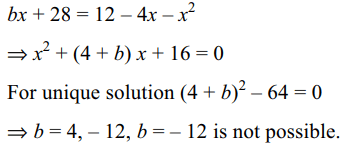
8. If \[2x^{2}+3x+4=0\] and \[ax^{2}+bx+c=0\] , where
\[a,b,c \epsilon N\] have a common root, then the least value
of a + b + c is
a) 10
b) 9
c) 8
d) 6
Explanation:
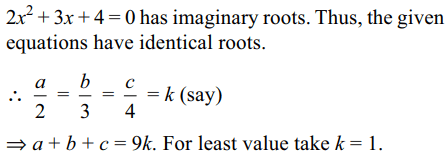
9. Let p, q, r, s be real numbers such that pr = 2(q +
s). Consider quadratic equations \[x^{2}+px+q=0\] and
\[x^{2}+rx+s=0\] . Then
a) none of these has real roots
b) both have real roots
c) at least one has real roots
d) at most one has real roots
Explanation:
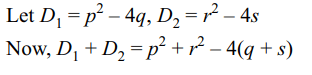

10. Let \[a< 0,a\neq -2\] . The equation \[x^{2}+a\mid x\mid+1=0\] has
a) no real roots
b) at least two real roots
c) exactly four real roots or no real roots
d) none of these
Explanation: