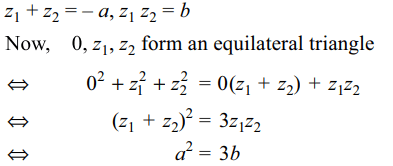1. Let L be the straight line \[\bar{a}z+a\bar{z}+c=0,a \neq0\] \[c\epsilon R \] , and OA be the straight line joining O and
A(a), then
a) \[L\parallel OA\]
b) \[L\perp OA\]
c) L makes an angle of \[\pi/4\] with OA
d) none of these
Explanation:

2. Locus of point z so that z, i, and iz are collinear, is
a) a straight line
b) a circle
c) an ellipse
d) a rectangular hyperbola
Explanation:
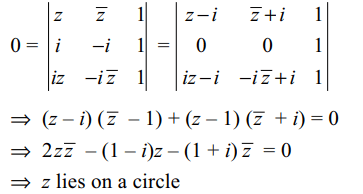
3. The number of roots of the equation \[\mid z^{2}\mid -5 \mid z\mid +1 =0\] is
a) 0
b) 2
c) 4
d) infinite
Explanation:
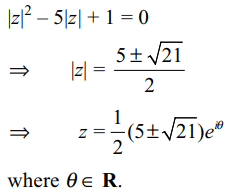
4.The set of points in C satisfying the inequality
\[\mid arg \left(z\right)-\pi/2\mid <\pi/2\] is given by
a) \[\left\{z: Re \left(z\right)> 0\right\}\]
b) \[\left\{z: In \left(z\right)< 0\right\}\]
c) \[\left\{z: Im \left(z\right)> 0\right\}\]
d) \[\left\{z: Re \left(z\right)=Im \left(z\right)\right\}\]
Explanation:
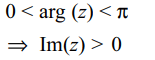
5.If n \[\geq\] 3 and \[1, \alpha_{1},\alpha_{2},...\alpha_{n-1}\] are nth roots of unity,
then value of \[\sum_{1\leq i < j \leq n-1}\alpha_{i}\alpha_{j}\] is
a) 0
b) 1
c) -1
d) \[\left(-1\right)^{n}\]
Explanation:
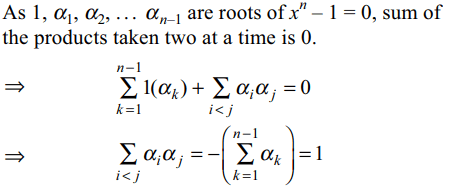
6. The Quadrilateral formed by the point with affix 0, z, z + iz and iz is
a) parallelogram
b) rhombus
c) rectangle
d) square
Explanation:

7. If |z – 2| = 2|z – 1|, then \[3|z|^{2} -4 Re \left(z\right)\] equals
a) 0
b) -1
c) 1
d) none of these
Explanation:
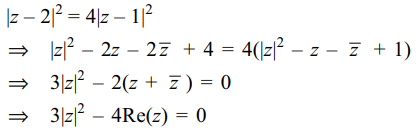
8. Sum of the common roots of \[z^{2006}+z^{100}+1=0\] and
\[z^{3}+2z^{2}+2z+1=0\] is
a) 0
b) -1
c) 1
d) 2
Explanation:
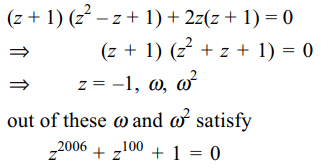
9. If \[z_{1}\] and \[z_{2}\] lie on the same side the line \[\bar{a}z+a\bar{z}+b =0\] ,
where \[a \epsilon C, a\neq 0,b\epsilon R\] , then the ratio \[\frac{\bar{a}z_{1}+a\bar{z}_{1}+b }{\bar{a}z_{2}+a\bar{z}_{2}+b }\] is
a) purely imaginary
b) a positive real number
c) a negative real number
d) none of these
Explanation:
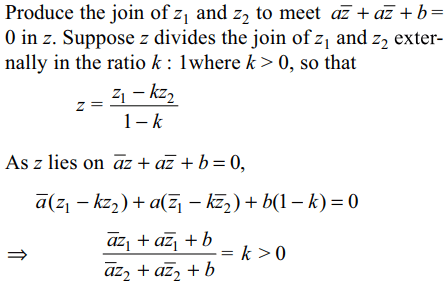
10.If \[z_{1}\] and \[z_{2}\] are the roots of the equation \[z^{2}+az+b=0\] , then prove that the origin, \[z_{1}\] and \[z_{2}\] form an
equilateral triangle if and only if
a) \[a^{2}=3b\]
b) \[b^{2}=3a\]
c) \[a^{2}+3b=0\]
d) \[b^{2}+3a=0\]
Explanation: