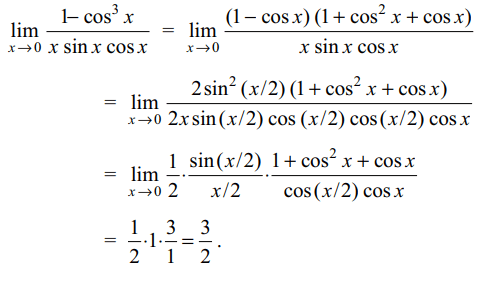1. \[\lim_{x \rightarrow 0}\left(\frac{1-\cos^{5}x}{1-\cos^{2}x}\right)\] is equal to
a) \[\frac{3}{2}\]
b) \[\frac{5}{2}\]
c) 1
d) 2
Explanation:
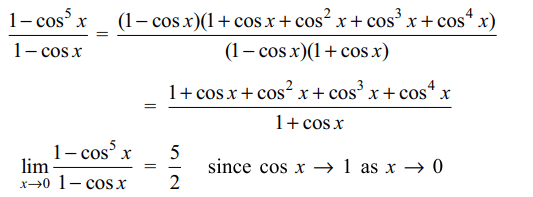
2. Let f(x)=\[\begin{cases}\frac{\frac{3}{x+1}+\sqrt{x+11}}{x+2}, & x \neq -2\\k, & x = -2\end{cases}\]
The value of k so that f is a continuous at x =-2 is
a) 2
b) \[\frac{11}{4}\]
c) \[\frac{17}{4}\]
d) \[-\frac{17}{6}\]
Explanation:
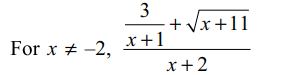
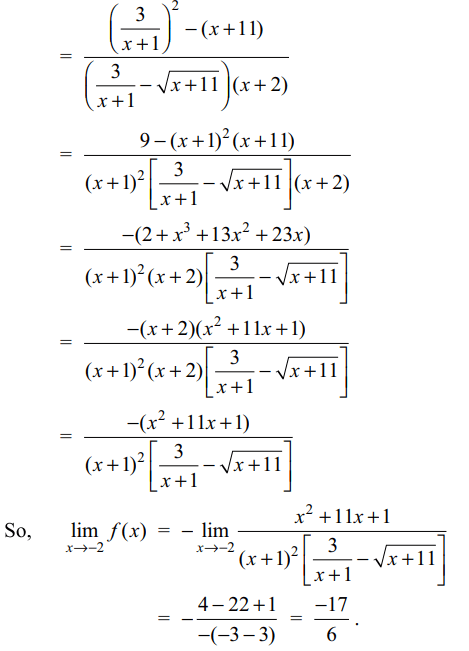
3. For a, b > 0 , the value of \[\lim_{n \rightarrow \infty}\left(4\left(\frac{a^{\frac{1}{n+1}}+b^{\frac{1}{n+1}}}{2}\right)^{n+1}-\left(\frac{a^{\frac{1}{n}}+b^{\frac{1}{n}}}{2}\right)^{n}\right)\]
is equal to
a) \[3\sqrt{ab}\]
b) \[\frac{1}{2}\sqrt{ab}\]
c) \[\sqrt{a}+\sqrt{b}\]
d) \[\sqrt{a}-\sqrt{b}\]
Explanation:
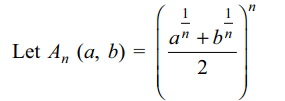
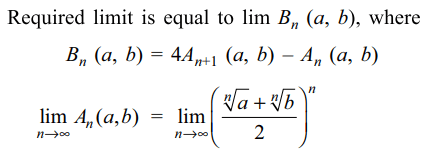
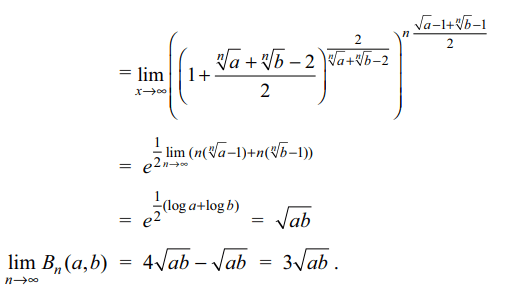
4. The value of \[\lim_{x \rightarrow 0}\log_{\tan^{2}x}\left(\tan^{2}2x\right)\] is
a) 2
b) 0
c) 1
d) \[\frac{1}{2}\]
Explanation:
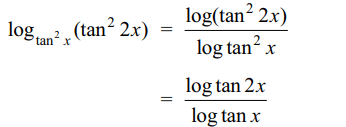
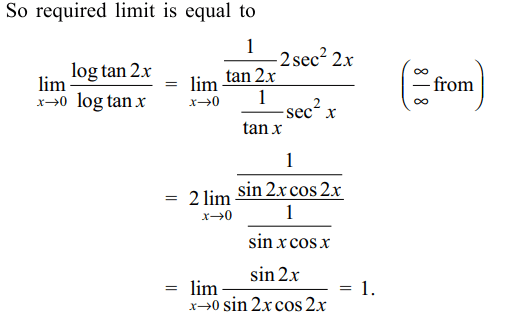
5. Let \[f\left(x\right)= \begin{cases}x+a & if & x < 0\\\mid x-1\mid & if & x \geq 0\end{cases}\]
and
\[g\left(x\right)= \begin{cases}x+1 & if & x < 0\\\left( x-1\right)^{2}+b& if & x \geq 0\end{cases}\]
The value of (a,b) so that gof is continuous
a) (1,1)
b) (2,1)
c) (1,2)
d) (1,0)
Explanation:
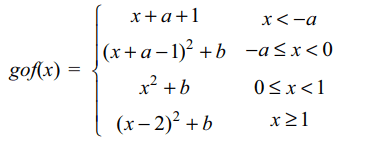
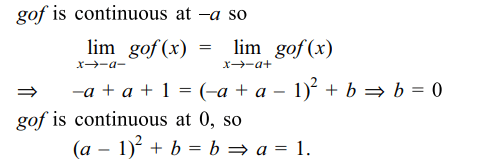
6. \[\lim_{x \rightarrow 0}\frac{\tan x-\sin x}{x^{3}}\] is
a) 0
b) 1/2
c) 2
d) none of these
Explanation:
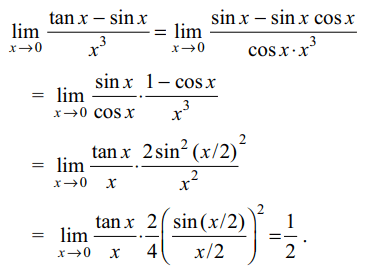
7. \[\lim_{n \rightarrow \infty}\left(\frac{1}{1-n^{2}}+\frac{2}{1-n^{2}}+....+\frac{n}{1-n^{2}}\right)\] is equal to
a) 0
b) -1/2
c) 1/2
d) none of these
Explanation:
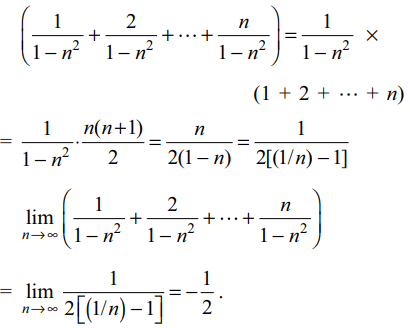
8. If \[f\left(x\right)=\begin{cases}\frac{\left[x\right]^{2}+\sin\left[x\right]}{\left[x\right]} & for\left[x\right] \neq 0\\0 & for \left[x\right] = 0\end{cases}\]
where [x] denoted the greatest integer less than or equal to x, then \[\lim_{x \rightarrow 0}f\left(x\right)\] equal
a) 1
b) 0
c) -1
d) \[\lim_{x \rightarrow 0+}f(x) =0\]
Explanation:
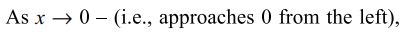
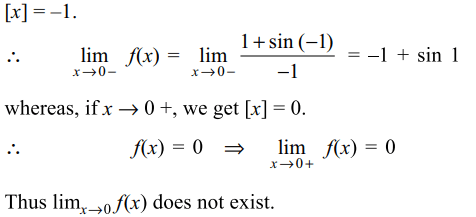
9. \[\lim_{x \rightarrow \pi/3}\frac{\sin\left(\pi/3-x\right)}{2\cos x-1}\] is equal to
a) 1/2
b) \[1/\sqrt{3}\]
c) \[\sqrt{3}\]
d) \[2/\sqrt{3}\]
Explanation:
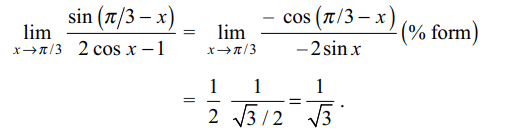
10. \[\lim_{x \rightarrow0}\frac{1-\cos^{3}x}{x \sin x \cos x}\] is equal to
a) 2/5
b) 3/5
c) 3/2
d) 3/4
Explanation: