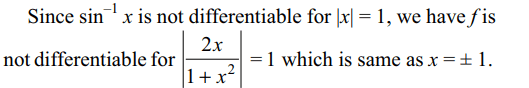1. Let \[g\left(x\right)=\frac{(x-1)^{n}}{\log\cos^{m}\left(x-1\right)};0< x< 2\]
and
m and n are integers, \[m\neq0,n>0\] , and let p be the left hand
derivative of | x – 1| at x = 1. If \[\lim_{x \rightarrow 1}g\left(x\right)=p\] then
a) n = 1, m = 1
b) n = 1, m - 1
c) n = 2, m = 2
d) n > 1, m = n
Explanation: Clearly p = – 1 and

2. Let f be a differentiable function satisfying
f (x + y) = f (x) + f (y) + xy(x + y) for all x, \[y\epsilon R\] . If f' (0) =
2, then
a) f is a polynomial function
b) f is a polynomial of degree 3 whose roots are 0, \[\pm i\sqrt{2}\]
c) f is thrice differentiable
d) All of the Above
Explanation: Differentiating w.r.t. x, keeping y constant
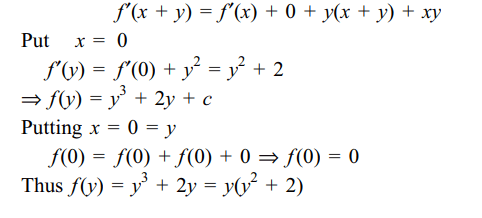
3. If \[f\left(x\right)=\begin{cases}\frac{\mid x+3\mid}{\tan^{-1}\left(x+3\right)} & x \neq-3\\4 & x = -3\end{cases}\]
then
a) f is continuous at x = –3
b) f is not derivable at x = –3
c) f is not continuous at x = –3
d) Both b and c
Explanation:
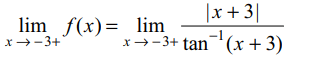
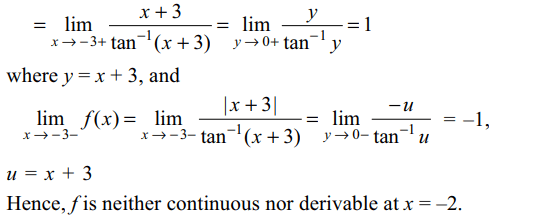
4.If x + | y | = 2y, then y as a function of x is
a) defined for all real x
b) continuous at x = 0
c) such that dy/dx = 1/3 for x < 0
d) All of the Above
Explanation: If x + | y | = 2y, then y can be written in terms of x as

5. The function f (x) = 1 + | sin x | is
a) continuous nowhere
b) continuous everywhere
c) not differentiable at x = 0
d) Both b and c
Explanation: Since g(u) = | u | and u(x) = sin x are continuous
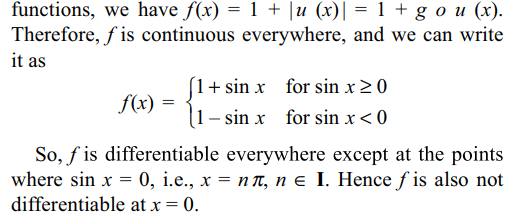
6. If \[f\left(x\right)=\sqrt{1-\sqrt{1-x^{2}}}\] , then
a) f is continuous on [-1,1]
b) f is continuous at x = 0
c) f is not differentiable at x = 0
d) All of the Above
Explanation: The domain of definition of this function is the

7. If \[f\left(x\right)=\begin{cases}\frac{x\log\cos x}{\log\left(1+x^{2}\right)} & x \neq 0\\0 & x = 0\end{cases}\]
then
a) f (x) is continuous at x = 0
b) f (x) is continuous at x = 0 but not differentiable
at x = 0
c) f (x) is derivable at x = 0 and f ' (0) = – 1/2
d) Both a and c
Explanation:
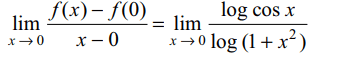
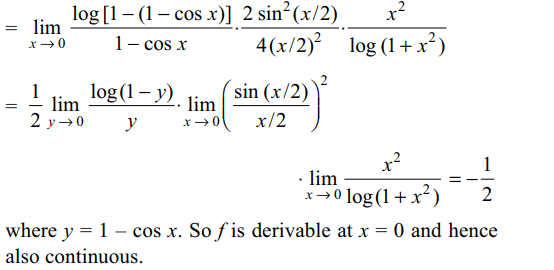
8. The function \[f\left(x\right)=\frac{x}{1+\mid x\mid}\] is differentiable
on
a) \[\left(0,\infty\right)\]
b) \[\left[0,\infty\right)\]
c) \[\left(-\infty,0\right)\]
d) All of the Above
Explanation: The given function can be written as

9. If \[f\left(x\right)=\begin{cases}x^{2}\cos\frac{1}{x} & x \neq 0\\0 & x = 0\end{cases}\]
then
a) f and f' are continuous at x = 0
b) f is derivable at x = 0
c) f is derivable at x = 0 and f' is not continuous at x=0
d) Both b and c
Explanation: For x \[\neq\] 0, we have
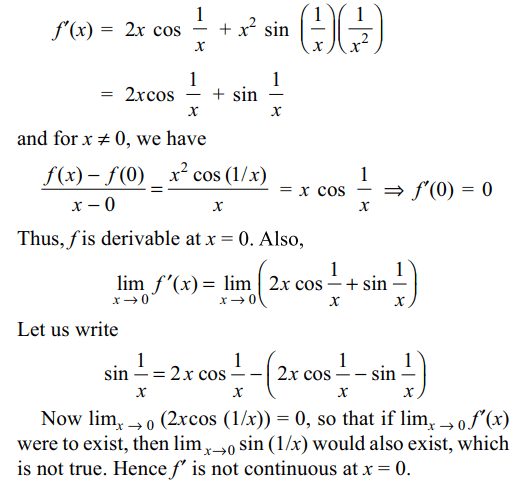
10. If \[f\left(x\right)=\sin^{-1}\frac{2x}{1+x^{2}}\] , then
a) f is derivable for all x, with | x | < 1
b) f is not derivable at x = 1
c) f is not derivable at x = – 1
d) All of the Above
Explanation: