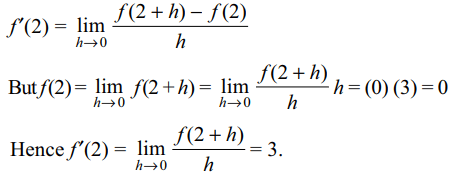1. If f'(x) = g(x) and g'(x) = - f (x) for all x and f (2) =
4 = f' (2) then \[f^{2}\left(8\right)+g^{2}\left(8\right)\] is
a) 16
b) 32
c) 64
d) 8
Explanation:
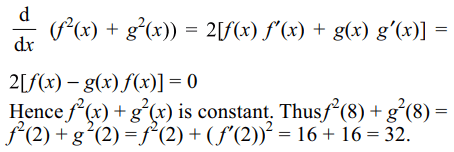
2. Let \[f\left(x\right)=\begin{cases}\sin^{2}x\left(\frac{e^{3/x}-e^{-3/x}}{e^{3/x}+e^{-3/x}}\right) & x \neq 0\\0 & x = 0\end{cases}\]
then
a) f is not continuous at x = 0
b) f is continuous but not differentiable at x = 0
c) f is differentiable at x = 0
d) f is differentiable at x = 0 and f'(0) = 3
Explanation:
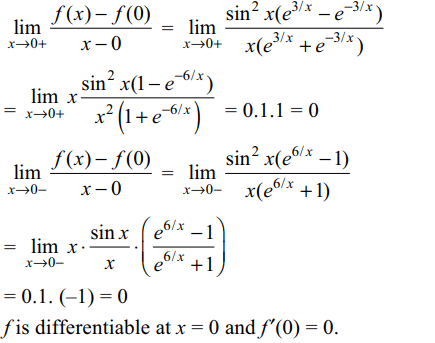
3. If \[x=2\sin t-\sin 2t,y=2\cos t-\cos2t,\]
then the
value of \[\frac{d^{2}y}{dx^{2}}\] at \[t=\pi\] is
a) 2
b) 1/8
c) -3/4
d) -3/2
Explanation:
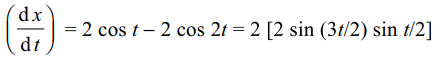

4. \[f\left(x\right)=\begin{cases}\mid x-4\mid & x \geq 1\\\left(x^{3}/2\right)-x^{2}+3x+1/2 & x < 1\end{cases}\]
then
a) f (x) is continuous at x = 1 and x = 4
b) f (x) is differentiable at x = 4
c) f (x) is continuous and differentiable at x = 1
d) f (x) is only continuous at x = 1
Explanation:

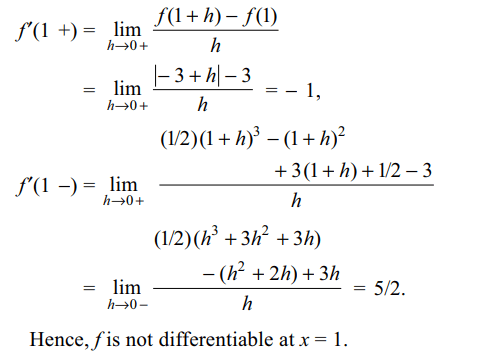
5. If \[f\left(x\right)=x^{2}+\frac{x^{2}}{\left(1+x^{2}\right)}+\frac{x^{2}}{\left(1+x^{2}\right)^{2}}+....+\frac{x^{2}}{\left(1+x^{2}\right)^{n}}+....\]
then at x =0
a) f (x) has no limit
b) f (x) is discontinuous
c) f (x) is continuous but not differentiable
d) (x) is differentiable
Explanation:

6. Let \[f\left(x\right)=\begin{cases}\int_{0}^{x}\left\{1+\mid 1-t\mid\right\}dt & x > 2\\5x-7 & x \leq 2\end{cases}\]
then
a) f is not continuous at x = 2
b) f is continuous but not differentiable at x = 2
c) f is differentiable everywhere
d) f'(2+) doesn’t exist
Explanation:
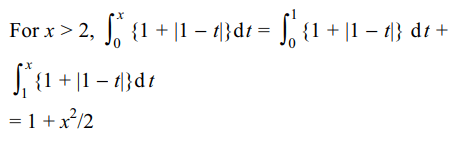

7. If \[f\left(x\right)=\mid \log_{5}\left(x^{3}+10x^{2}+11x-69\right)\mid\]
then at x = 2
a) f is not continuous
b) f is continuous but not differentiable
c) f is differentiable
d) the derivative is 1
Explanation:

8. If f''(x) is continuous at x = 0 and f ''(0) = 5, then the
value of \[\lim_{x \rightarrow 0}\frac{2f\left(x\right)-3f\left(2x\right)+f\left(4x\right)}{x^{2}}\]
is
a) 10
b) 8
c) 15
d) 12
Explanation:

9. The solution set of f'(x) > g'(x) where \[f\left(x\right)=\left(1/2\right)5^{2x+1}\] and \[g\left(x\right)=5^{x}+4x \log 5\]
is
a) \[\left(1,\infty\right)\]
b) \[\left(0,1\right)\]
c) \[\left[0,\infty\right)\]
d) \[\left(0,\infty\right)\]
Explanation:
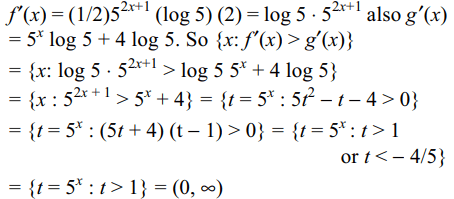
10. Suppose f is differentiable at x = 2 and \[\lim_{h \rightarrow0}\frac{f\left(2+h\right)}{h}=3\]
then
a) f '(2) = 4
b) f '(2) = 5
c) f '(2) = 6
d) f '(2) = 3
Explanation: