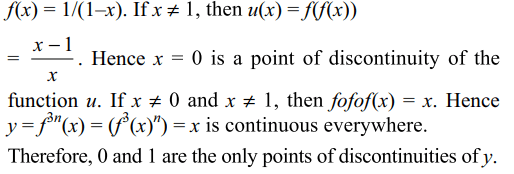1. \[\lim_{x \rightarrow 0}\frac{\sin\left(\pi\cos^{2}x\right)}{x^{2}}\] equals
a) \[-\pi\]
b) \[\pi\]
c) \[\pi/2\]
d) 1
Explanation:
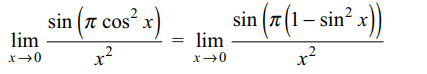
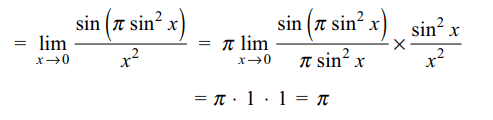
2. For \[x \epsilon R ,\lim_{x \rightarrow \infty}\left(\frac{x-3}{x+2}\right)^{x}=\]
a) e
b) \[e^{-1}\]
c) \[e^{-5}\]
d) \[e^{5}\]
Explanation:
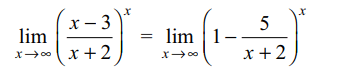
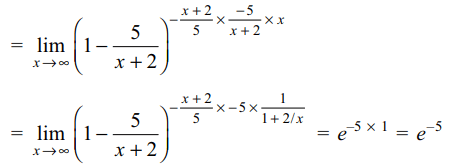
3. The integer n for which \[\lim_{x \rightarrow0}\frac{(\cos x-1)\left(\cos x-e^{x}\right)}{x^{n}}\] is a finite nonzero number is
a) 1
b) 2
c) 3
d) 4
Explanation:


4. If f(x) = (x/2) – 1, then on the interval \[\left[0,\pi\right]\]
a) \[\tan (f\left(x\right))\] and \[\frac{1}{f\left(x\right)}\] are both continuous
b) \[\tan (f\left(x\right))\] and \[\frac{1}{f\left(x\right)}\] are both discontinuous
c) \[\tan (f\left(x\right))\] and \[f^{-1}\left(x\right)\] are both continuous
d) neither \[\tan (f\left(x\right))\] nor \[f^{-1}\left(x\right)\] is continuous
Explanation: f (x) = (x/2) - 1 is continuous on [0, \[\pi\] ] and
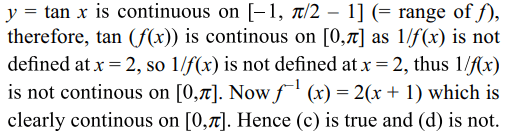
5. The value of \[\lim_{x \rightarrow \beta}\frac{1-\cos\left(ax^{2}+bx+c\right)}{\left(x-\beta\right)^{2}}\]
where
\[\alpha,\beta\] are the distinct roots of \[ax^{2}+bx+c=0\] is
a) \[\left(\alpha-\beta\right)^{2}\]
b) \[\frac{\left(\alpha-\beta\right)^{2}}{2}\]
c) \[\left(\frac{a\left(\alpha-\beta\right)}{2}\right)^{2}\]
d) none of these
Explanation:

6. \[\lim_{x \rightarrow a}\left\{\left[\left(\frac{a^{1/2}+x^{1/2}}{a^{1/4}-x^{1/4}}\right)^{-1}-\frac{2\left(ax\right)^{1/4}}{x^{3/4}-a^{1/4}x^{1/2}+a^{1/2}x^{1/4}-a^{3/4}}\right]^{-1}-\sqrt{2}^{\log_{4}{a}}\right\}^{8}\]
is
a) a
b) \[a^{3/4}\]
c) \[a^{2}\]
d) none of these
Explanation: Simplifying the expression in brackets by setting a1/4 = b and x1/4 = y, the function whose limit is required can be written as

7. The value of a for which \[\frac{\sin 2x+a\sin x}{x^{3}}\] tends to a finite limits as \[x\rightarrow 0\] is
a) 1
b) 2
c) -3
d) none of these
Explanation: Since numerator as well as denominator both
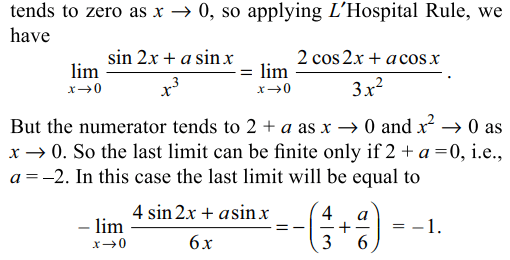
8. If g(x) is a polynomial satisfying g(x) g(y)
= g(x) + g(y) + g(xy) -2 for all real x and y and g(2) =5 then \[\lim_{x \rightarrow 3}\] g(x) is
a) 9
b) 25
c) 10
d) none of these
Explanation: Putting x = 2 and y = 1, we have
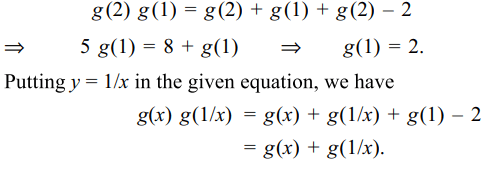
g(x) = xn+1 or g(x)
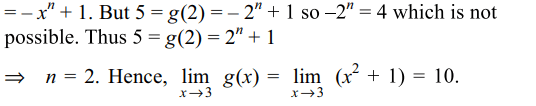
9. Let \[f:R\rightarrow R\] be a function such that \[f\left(\frac{x+y}{2}\right)=\frac{f\left(x\right)+f\left(y\right)}{2}\] for all x and y , and f(0)= 3 and f'(0) = 3 then
a) \[f\left(x\right)\] /x is continuous on R
b) \[f\left(x\right)\] is continuous on R
c) \[f\left(x\right)\] is bounded on R
d) none of these
Explanation:


10. Given the function f(x) = 1/(1 – x), the number points of discontinuity of the
composite function \[y=f^{3n}\left(x\right),\] where \[f^{n}\left(x\right)=fof\] .... of (n
times ) are \[\left(n\epsilon N\right)\]
a) 0 , 1
b) 2n
c) 3n
d) 2n+1
Explanation: The point x = 1 is a discontinuity of the function