PrepBharat

1. Let f (x) be defined by
\[f\left(x\right)=\begin{cases}\sin 2x & 0< x \leq\pi/6\\ax+b & \pi/6 < x< 1\end{cases}\]
The values of a and b such that f and f' are continuous are
a) \[a=1 , b=\frac{1}{\sqrt{2}}+\frac{\pi}{6}\]
b) \[a=\frac{1}{\sqrt{2}}=b\]
c) \[a=1 , b=\frac{\sqrt{3}}{2}-\frac{\pi}{6}\]
d) \[a=1, b=\frac{1}{2}-\frac{\pi}{6}\]

View Answer

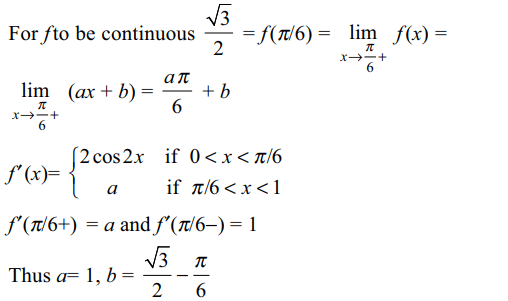
2. The coefficients a and b that make the function \[f\left(x\right)=\begin{cases}1/\mid x\mid & \mid x\mid\geq 1\\ax^{2}+b &\mid x\mid< 1\end{cases}\]
differentiable at any point are given by
a) a = - 1/2, b = 3/2
b) a = 1/2, b = - 3/2
c) a = 1, b = - 1
d) a = 1/2, b = 3/4

View Answer

3. The derivative at x = 0 of \[\tan^{-1}\frac{\sqrt{1+x^{2}}-1}{x}\]    w.r.t. \[\tan^{-1}\frac{2x\sqrt{1+x^{2}}}{1-2x^{2}}\]
is
a) 1/4
b) 1/8
c) 1/2
d) 1

View Answer

4. If \[y=\sin^{-1}\sqrt{\frac{1-x}{1+x}}\]    then y '(1/2) is equal to
a) 1
b) 1/2
c) \[-\sqrt{2}/3\]
d) \[-2\sqrt{2}/3\]

View Answer

5. If \[y=\sqrt{\frac{1-\sin^{-1}x}{1+\sin^{-1}x}}\]    then y'(0) is equal to
a) 1
b) 1/2
c) -1
d) \[\sqrt{2}/3\]

View Answer

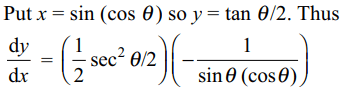
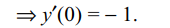
6.Let \[f\left(x\right)=e^{ax}\sin\left(bx+c\right)\]     and \[f''\left(x\right)=r^{2}e^{ax}\sin\left(bx+\theta\right)\]
then
a) \[r=a^{2}+b^{2}\]
b) \[r=\sqrt{a^{2}+b^{2}}\]
c) \[\theta=c+2\tan^{-1}\left(b/a\right)\]
d) Both b and c

View Answer

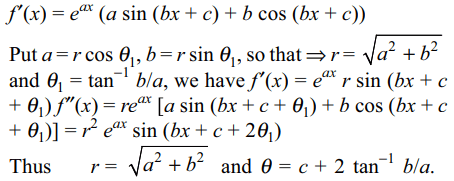
7. Let f be a function satisf ying f (x + y) = f (x) f (y) for all x and y and f (0) = f '(0) = 1 then
a) f is differentiable for all x
b) f '(x) = f (x)
c) \[f\left(x\right)=e^{x}\]
d) All of the Above

View Answer

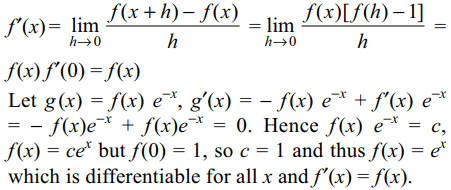
8. Let f(x) = \[x+\mid x \mid+\cos(\left[2\pi^{2}\right]x) \]     and h(x) = \[\cos\left[\pi^{2}\right]x\]    where [.] denotes the greatest integer function. Then
a) f+ g is continuous everywhere but not differentiable at x = 0
b) f+ g is differentiable at x = 0
c) fg is continuous but not differentiable at x = 0
d) Both a and c

View Answer

9. Let \[f\left(x\right)=\begin{cases}x^{2}sgn\left[x\right]+\left\{x\right\} & 0\leq x< 2\\\sin x+\mid x-3 \mid & 2\leq x< 4\end{cases}\]
wher [x] and {x} denote the greatest integer and fractional part functions. Then
a) f is discontinuous at x = 2
b) f is continuous but not differentiable at x = 1
c) f is not differentiable at x = 2
d) All of the Above

View Answer

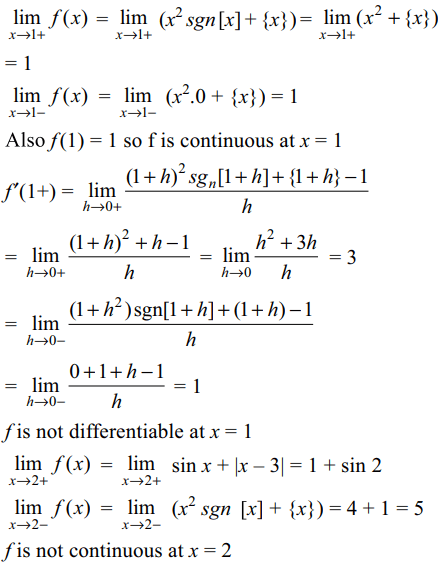
10. Let \[y=x^{8}+e^{x}\]   then
a) \[y_{10}=y_{12}\]
b) \[y_{10}=y_{11}\]
c) \[y_{11}=y_{14}\]
d) All of the Above

View Answer