1. Let \[f:R\rightarrow R\] be given by f(x) = 5x , if \[x\epsilon Q\] and \[f\left(x\right)=x^{2}+6\] if \[x\epsilon R \sim Q\] then
a) f is continuous at x=1 and x=2
b) f is not continuous at x=1 and x=2
c) f is continuous at x=1 but not at x=2
d) f is continuous at x=2 but not at x=1
Explanation:
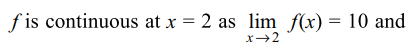
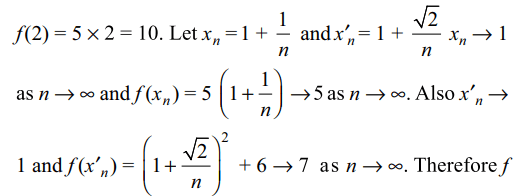
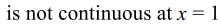
2. If \[\lim_{x \rightarrow 0}\frac{\left(\left(a-n\right)nx-\tan x\right)\sin n x}{x^{2}}=0\]
where \[ n\epsilon R \sim\left\{0\right\}\] then a is equal to
a) 0
b) \[\frac{n}{n+1}\]
c) n
d) n+1/n
Explanation:

3. Let \[f\left(x\right)=\lim_{n \rightarrow \infty} \frac{x}{x^{2n}+1}\] then
a) \[\lim_{x \rightarrow 1+} f\left(x\right)+\lim_{x \rightarrow 1-} f\left(x\right)=1\]
b) \[\lim_{x \rightarrow 1+} f\left(x\right)+\lim_{x \rightarrow 1-} f\left(x\right)+f\left(1\right)=\frac{3}{2}\]
c) \[\lim_{x \rightarrow 1+} f\left(x\right)+\lim_{x \rightarrow 1-} f\left(x\right)=0\]
d) All of the Above
Explanation:

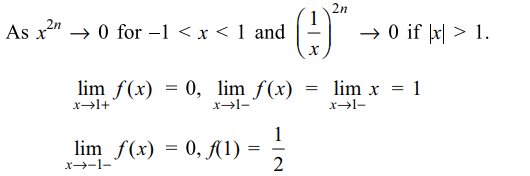
4. If \[f\left(x\right)=\left(\frac{x}{3+x}\right)^{x}\] , then
a) \[\lim_{x \rightarrow \infty} f\left(x\right)=e^{-3}\]
b) \[\lim_{x \rightarrow 1} f\left(x\right)=1/4\]
c) \[\lim_{x \rightarrow \infty} f\left(x\right)=e^{-5}\]
d) Both a and b
Explanation:

5. If \[f\left(x\right)=x\frac{e^{\left[x\right]+\mid x\mid}-2}{\left[x\right]+\mid x\mid}\] then
a) \[\lim_{x \rightarrow 0+}f\left(x\right)=-1\]
b) \[\lim_{x \rightarrow 0-}f\left(x\right)=0\]
c) \[\lim_{x \rightarrow 0}f\left(x\right)\] does not exist
d) All of the Above
Explanation:
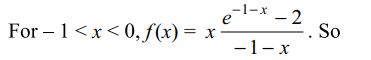

6. The \[\lim_{x \rightarrow 0}x^{8}\left[\frac{1}{x^{3}}\right]\] ( where [x] is greatest integer function) is
a) zero
b) a rational number
c) an integer
d) All of the Above
Explanation:
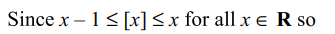

7. If \[f\left(x\right)=\lim_{n \rightarrow\infty}\left(\sin x\right)^{2n}\] , then f is
a) continuous at \[x =\pi\]
b) discontinuous at \[x =\pi/2\]
c) discontinuous at \[x =-\pi/2\]
d) All of the Above
Explanation:


8. Let f(x) be defined on \[\left[0,\pi\right]\] by
\[f\left(x\right)=\begin{cases}x+a\sqrt{2}\sin x & ,0\leq x\leq\pi/4\\2x\cot x+b&\ ,\pi/4< x\leq\pi/2 \\a\cos2x-b\sin x &\ ,\pi/2< x\leq\pi \end{cases}\]
If f is continuous on \[\left[0,\pi\right]\] then
a) \[a=\pi/6\]
b) \[b=-\pi/12\]
c) \[a=\pi/6\] and \[b-\pi/12\]
d) All of the Above
Explanation:


9. Let \[f\left(x\right)=g'\left(x\right)\frac{e^{a/x}-e^{-a/x}}{e^{a/x}+e^{-a/x}}\] where g' is the derivative of g and is a continuous function and a> 0 then \[\lim_{x \rightarrow 0}f(x)\] exist if
a) g(x) is polynomial
b) \[g\left(x\right)=x^{3}\] h(x) where h(x) is a polynomial
c) \[g\left(x\right)=x^{2}\]
d) Both b and c
Explanation:

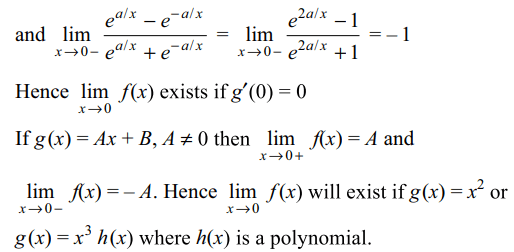
10. Let \[f\left(x\right)=\left[x\right]+\left[-x\right]\] . then for any integer n and \[ k \epsilon R \sim I\]
a) \[\lim_{x \rightarrow n}f\left(x\right)\] exists
b) \[\lim_{x \rightarrow k}f\left(x\right)\] exists
c) f is continuous at x = k
d) All of the Above
Explanation:

