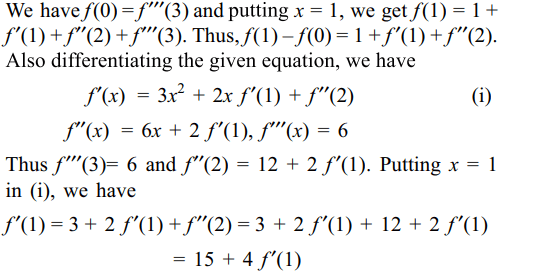PrepBharat

1. If \[f"\left(x\right)=\frac{\cos\left(\log x\right)}{x},f'\left(1\right)=0\]      and \[y=f\left(\frac{2x+3}{3-2x}\right)\]   , then \[\frac{dy}{dx}\mid x=1\]    is equal to
a) 4 sin (log 4))
b) 15 sin log 5
c) 12 sin (log 5)
d) 9 sin log 7

View Answer

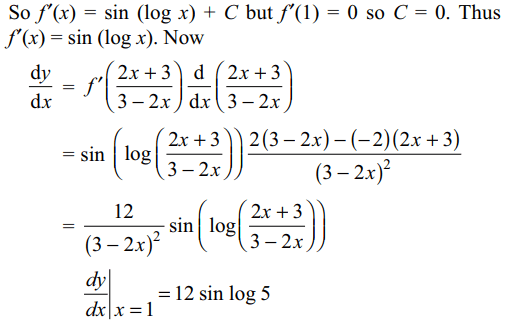
2. Which of the following could be not true If \[f"\left(x\right)=x^{-1/3}\]
a) \[f\left(x\right)=\frac{3}{2}x^{2/3}-3\]
b) \[f\left(x\right)=\frac{9}{10}x^{5/3}-7\]
c) \[f'''\left(x\right)=-\frac{1}{3}x^{-4/3}\]
d) \[f'\left(x\right)=\frac{3}{2}x^{2/3}+6\]

View Answer

3. Suppose that f(x)=[x]', the least integer function then
a) f is differentiable on [0,4]
b) there is a differentiable function on \[(- \infty, \infty)\]   whose derivative is f (x).
c) f is continuous on [0,1)
d) f is differentiable on [0,1]

View Answer

4. If \[y=e^{\sqrt{x}}+e^{-\sqrt{x}}\]     then \[xy_{2}+\left(1/2\right)y_{1}\]    is equal to
a) y
b) \[x\left(e^{\sqrt{x}}+e^{-\sqrt{x}}\right)\]
c) \[\left(1/4\right) y\]
d) \[\sqrt{x}y\]

View Answer

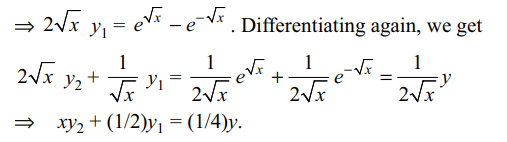
5. If \[y=\cos^{-1}\frac{x^{2n}-1}{x^{2n}+1}\]
then y'(x) is equal to
a) \[\frac{2n x^{n-1}}{x^{2n}+1}\]   If n is even
b)\[\frac{2n x^{n}}{\mid x\mid\left(x^{2n}+1\right)}\]   If n is odd
c) \[-\frac{2n x^{n}}{\mid x\mid\left(x^{2n}+1\right)}\]   If n is odd
d) \[\frac{2n x^{n-1}}{\left(x^{2n}+1\right)}\]

View Answer

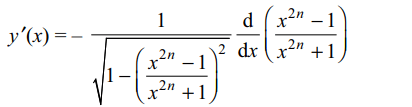
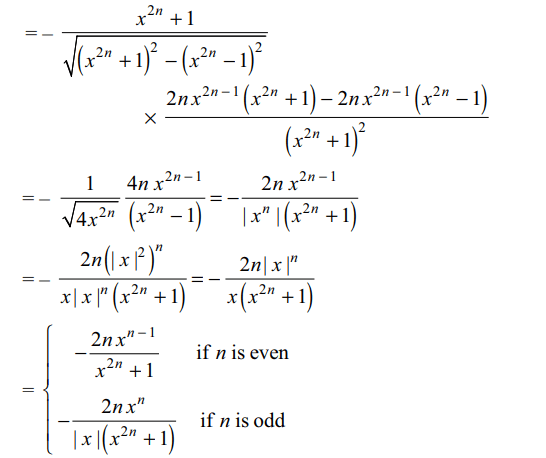
6. If \[y\left(n,x\right)=e^{x}e^{x^{2}}....e^{x^{n}},0< x < 1 \]
Then \[\lim_{n \rightarrow\infty}\frac{dy\left(n,x\right)}{dx}\]   at x = 1/2 is
a) e
b) 4e
c) 2e
d) 3e

View Answer

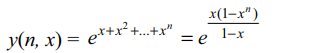
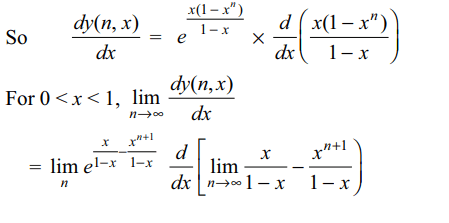
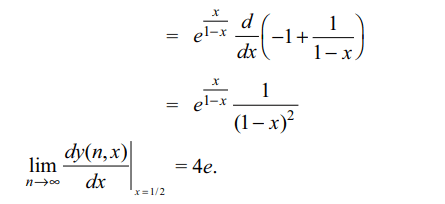
7. If \[x=a \cos t,y=a\sin t\]      then \[\frac{d^{3}y}{dx^{3}}\] at \[t=\frac{\pi}{4}\]  is
a) \[3/a^{2}\]
b) \[-12/a^{2}\]
c) \[-3/a^{2}\]
d) \[12/a^{2}\]

View Answer

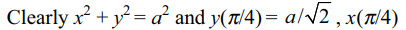
8. If \[\cos^{-1}\left(\frac{x^{2}-y^{2}}{x^{2}+y^{2}}\right)=\log a\]      then \[\frac{dy}{dx}\] is
a) y/x
b) x/y
c) \[x^{2}/y^{2}\]
d) \[y^{2}/x^{2}\]

View Answer

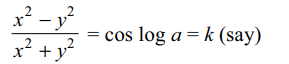
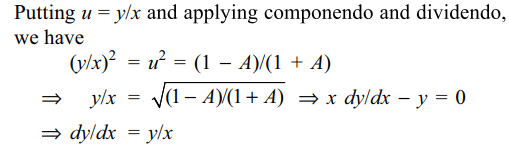
9. Let \[f\left(\frac{x+y}{2}\right)=\frac{1}{2}\left[f\left(x\right)+f\left(y\right)\right]\]      for real x and y. If f' (0) exists and equals - 1 and f (0) = 1 then the value of f (2) is
a) 1
b) -1
c) 1/2
d) 2

View Answer

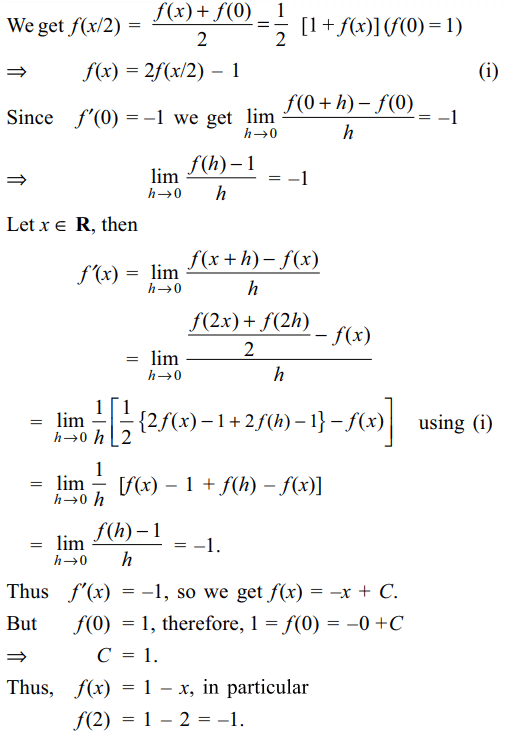
10. If \[f:R\rightarrow R\]   is a function such that \[f\left(x\right)=x^{3}+x^{2}f'\left(1\right)+xf"\left(2\right)+f'''\left(3\right)\]
for \[x\epsilon R\]  then the value of f (2) is
a) 5
b) 10
c) 6
d) -2

View Answer