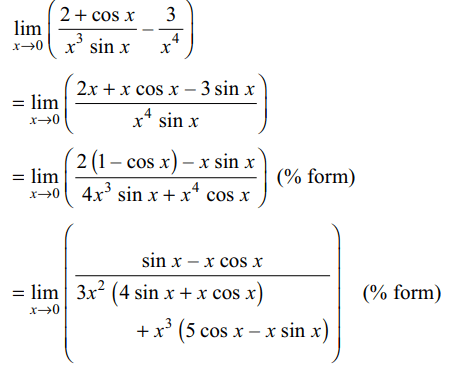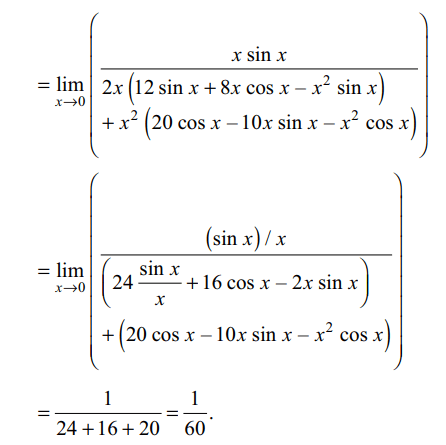1. The value of \[\lim_{x \rightarrow 0}\frac{\sqrt{x^{2}+1}-1}{\sqrt{x^{2}+9}-3}\] is
a) 4
b) 3
c) 1
d) 2
Explanation:
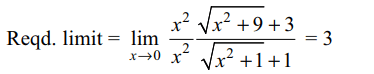
2. The value of \[\lim_{x \rightarrow b}\frac{\sqrt{x-a-}\sqrt{b -a}}{x^{2}-b^{2}}\left(b> a\right)\] is
a) \[\frac{1}{4b}\]
b) \[\frac{1}{b\sqrt{b-a}}\]
c) \[\frac{1}{2b\sqrt{b-a}}\]
d) \[\frac{1}{4b\sqrt{b-a}}\]
Explanation:
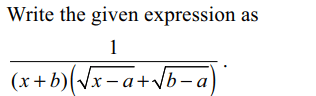
3. If \[f\left(x\right)=\frac{\log\left(e^{x^{2}}+2\sqrt{x}\right)}{\tan\sqrt{x}},x\neq0.\]
The value of
\[\lim_{x \rightarrow 0}f\left(0\right)\] is
a) \[\frac{1}{2}\]
b) \[\sqrt{2}\]
c) 2
d) \[\frac{1}{\sqrt{2}}\]
Explanation:
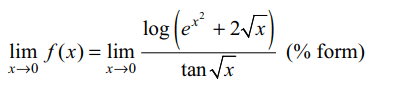
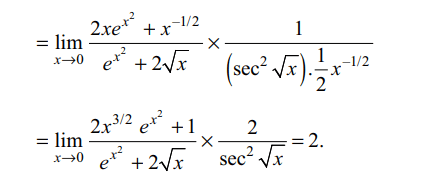
4. The value of \[\lim_{x \rightarrow \infty}\frac{\left(x+1\right)^{20}+\left(x+2\right)^{20}+....+\left(x+100\right)^{20}}{x^{20}+10^{20}}\]
is
a) 100
b) 1
c) 10
d) 20
Explanation:
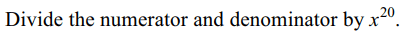
5. If \[f\left(x\right)=\left(\frac{x^{2}+4x+3}{x^{2}+x+2}\right)^{x}\] , then
\[\lim_{x \rightarrow \infty}f\left(x\right)\] is
a) \[e^{3}\]
b) \[e^{4}\]
c) \[e^{2}\]
d) \[2^{4}\]
Explanation:
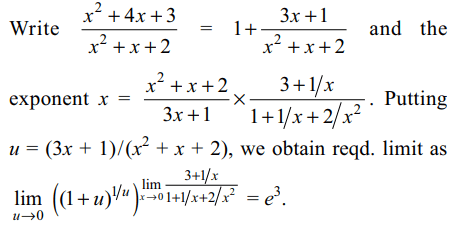
6. Let \[f\left(x\right)=\left(\tan \left(\pi/4-x\right)/\cot 2x\right)\left(x\neq\pi/4\right).\]
The value which should be
assigned to f at \[x=\pi/4\] , so that it is continuous everywhere , is
a) 1/2
b) 1
c) 2
d) 1/4
Explanation:
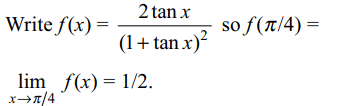
7. Let \[f\left(x\right)=\frac{x \tan 2x-2x\tan x}{\left(1-\cos 2x\right)^{2}},x\neq0\]
Then the value
f(0) so that f is continuous
a) 2
b) -2
c) 1/2
d) -1/2
Explanation:

8. \[\lim_{x \rightarrow 1}\frac{1+\log x-x}{1-2x+x^{2}}\] equals
a) 1
b) 0
c) -1
d) -1/2
Explanation:

9. Let f be a continuous function satisfying f(x) f(y) = f (x) + f(y) + f (xy) – 2 for all
x, \[ y\epsilon R\] and f(2) = 5 then \[\lim_{x \rightarrow 4}f\left(x\right)\] is
a) 5
b) 17
c) -5
d) 21
Explanation:
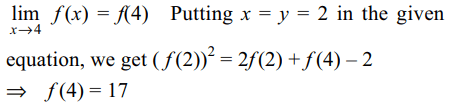
10. The value of \[\lim_{x \rightarrow 0}\left(\frac{2+\cos x}{x^{3}\sin x}-\frac{3}{x^{4}}\right)\] is
a) \[\frac{1}{30}\]
b) 0
c) \[\frac{1}{60}\]
d) none of these
Explanation: