1. suppose that f is a differentiable function with the
property that f (x + y) = f (x) + f (y) + xy and f '(0) = 5 then
a) f is a linear function
b) \[f\left(x\right)=3x+x^{2}\]
c) \[f\left(x\right)=5x+x^{2}/2\]
d) \[f\left(x\right)=x+\frac{5x^{2}}{2}\]
Explanation:


2. If \[f\left(a\right)=a^{2},\phi\left(a\right)=b^{2}\] and \[f'\left(a\right)=5\phi' (a)\] then \[\lim_{x \rightarrow 0}\frac{\sqrt{f\left(x\right)}-a}{\sqrt{\phi\left(x\right)}-b}\]
is
a) \[b^{2}/a^{2}\]
b) b/a
c) 2b/a
d) 5b/a
Explanation:
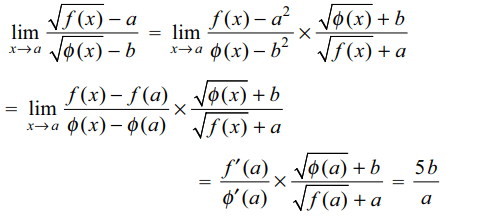
3. If \[y=\cot^{-1}\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\]
then \[\frac{d^{2} y}{dx^{2}}\] is
equal to
a) 0
b) 1/2
c) \[\frac{1}{1+\sin x}\]
d) \[\frac{1}{\sqrt{1+\sin x}}+\frac{1}{\sqrt{1-\sin x}}\]
Explanation:
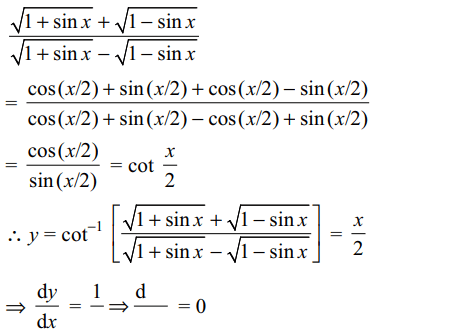
4. If \[x=\cos\theta,y=\sin^{3}\theta\] , then
\[\left(\frac{d y}{dx}\right)^{2}+y\frac{d^{2} y}{dx^{2}}\] at
\[\theta=\pi/4\] is
a) 1
b) 2
c) -2
d) 9/4
Explanation:

5. If \[y=\tan^{-1}\frac{1}{1+x+x^{2}}+\tan^{-1}\frac{1}{x^{2}+3x+3}+\tan^{-1}\frac{1}{x^{2}+5x+7}+....+\]
upto n terms, then
y'' (0) is equal to
a) \[-1/\left(n^{2}+1\right)^{2}\]
b)\[-n^{2}/\left(n^{2}+1\right)^{2}\]
c) \[n^{2}/\left(n^{2}+1\right)^{2}\]
d) 0
Explanation:
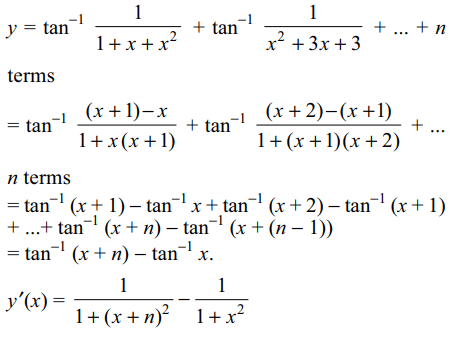
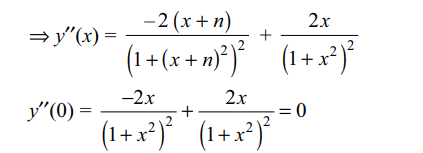
6. If \[\left(\sin x\right)\left(\cos y\right)=\frac{1}{2}\] then \[d^{2}y/dx^{2}\] at \[\left(\pi/4,\pi/4\right)\] equal
to
a) -4
b) -2
c) -6
d) 0
Explanation:

7. If x = sin t, y = sin kt satisfies \[\left(1-x^{2}\right)y_{2}-xy_{1}+Ay=0\]
then A is equal to
a) k
b) 1
c) \[k^{2}\]
d) 1+k
Explanation:
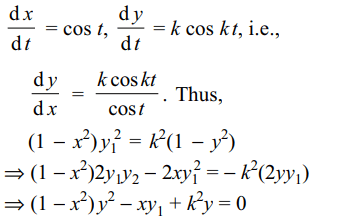
8. Let \[f\left(x\right)=\begin{cases}x^{2}/2 & if 0\leq x\leq1\\2x^{2}-3x+3/2 &if 1\leq x\leq 2\end{cases}\]
then
a) f' is not a continuous function
b) f'' is not continuous at x = 1
c) f is not differentiable at x = 1
d) f is not continuous at x = 1
Explanation:

9. Let f and g be differentiable function satisf ying g'(a)
= 2, g(a) = b and f o g = I (identity function). Then
f '(b) is equal to
a) 1/2
b) 2
c) 2/3
d) 3/4
Explanation:
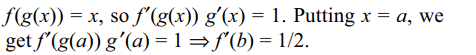
10. If \[y=x^{n}\left(a\cos\left(\log x\right)+b\sin\left(\log x\right)\right)\] and y satisfies \[y_{2}+\left(1-2n\right)xy_{1}+Ay=0\]
then A is equal to
a) n
b) \[1+n^{2}\]
c) 1+1/n
d) \[1-n^{2}\]
Explanation:
