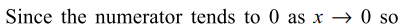1. If \[f\left(x\right)=\begin{cases}\left(1+\mid\sin x\mid\right)^{a/\mid\sin x\mid} & - \pi/6< x < 0\\b&\ x=0 \\e^{\tan 2x/\tan 3x} &\ 0< x< \pi/6 \end{cases}\]
is a continuous function on \[\left(-\pi/6,\pi/6\right)\] , then
a) \[a = 2/3, b = e^{2}\]
b) \[a = 1/3, b = e^{1/3}\]
c) \[a = 2/3, b = e^{2/3}\]
d) None of these
Explanation:
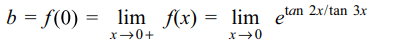
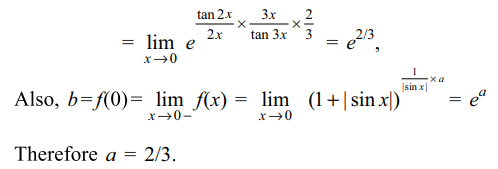
2. Let \[f\left(x\right)=\lim_{n \rightarrow \infty}\frac{\log\left(2+x\right)-x^{2n}\sin x}{1+x^{2n}},\]
then
a) f is continuous at x=1
b) \[\lim_{x \rightarrow1+}f\left(x\right)\neq \lim_{x \rightarrow1-}f\left(x\right)\]
c) \[\lim_{x \rightarrow1+}f\left(x\right)=\sin 1\]
d) \[\lim_{x \rightarrow1-}f\left(x\right)\] doesn't exist
Explanation:
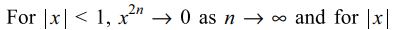
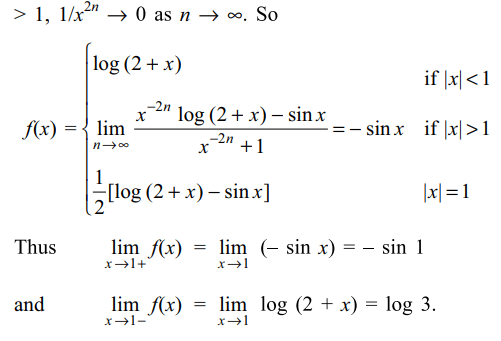
3. Let \[f\left(x\right)=g\left(x\right)\frac{e^{1/x}-e^{-1/x}}{e^{1/x}+^{-1/x}}\] and
\[x\neq0\] where g is a continuous function. Then \[\lim_{x \rightarrow 0}\] f(x) exists if
a) g(x) is any polynomial
b) g(x) = x + 4
c) \[f\left(x\right)=x^{2}\]
d) \[f\left(x\right)=2+3x+4x^{2}\]
Explanation:

4. The value of \[\lim_{n \rightarrow \infty } \cos\frac{x}{2}\cos\frac{x}{4}....\cos\frac{x}{2^{n}}\] is
a) 1
b) \[\frac{\sin x}{x}\]
c) \[\frac{x}{\sin x}\]
d) None of these
Explanation:
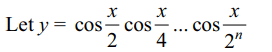

5. Let f be continuous function on R such that \[f\left(\frac{1}{4n}\right)=\left(\sin e^{n}\right)e^{-n^2}+\frac{n^{2}}{n^{2}+1}.\]
Then the value of f(0) is
a) 1
b) 1/2
c) 0
d) None of these
Explanation:
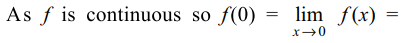
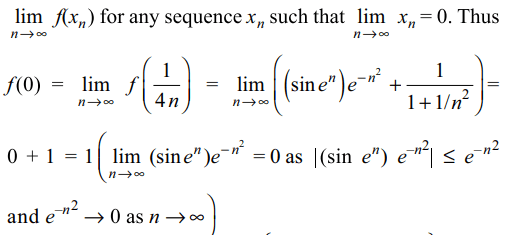
6. Let \[f\left(x\right)=\left\{\frac{\log \left(1+x\right)^{1+x}}{x^{2}}-\frac{1}{x}\right\}\]
Then the value of f(0) so that the function f is continuous is
a) 1
b) 1/2
c) 2/4
d) None of these
Explanation:
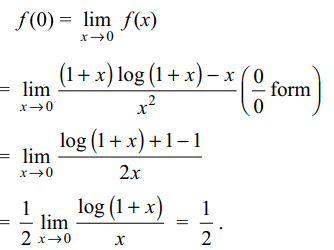
7. If \[\lim_{x \rightarrow a}(f\left(x\right)g\left(x\right))\] exists for any functions f and g then
a) \[\lim_{x \rightarrow a}f\left(x\right)\] and \[\lim_{x \rightarrow a}g\left(x\right)\] exist
b) \[\lim_{x \rightarrow a}f\left(x\right)\] exist but \[\lim_{x \rightarrow a}g\left(x\right)\] may not exist
c) \[\lim_{x \rightarrow a}f\left(x\right)\] mayn't exist but \[\lim_{x \rightarrow a}g\left(x\right)\] exist
d) \[\lim_{x \rightarrow a}f\left(x\right)\] and \[\lim_{x \rightarrow a}g\left(x\right)\] may not exist
Explanation:
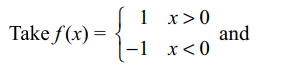

8. The value of \[\lim_{x \rightarrow 0}\frac{\left(1+x\right)^{1/x}-e+\frac{1}{2}ex}{x^{2}}\] is
a) \[\frac{11}{24}e\]
b) \[-\frac{11}{24}e\]
c) \[\frac{e}{24}\]
d) None of these
Explanation:
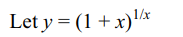
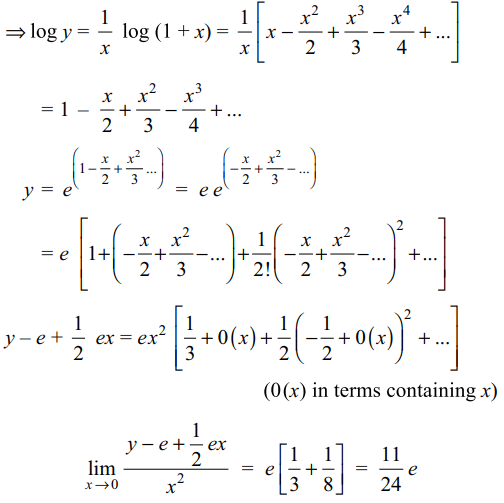
9. The value of \[\lim_{x \rightarrow 0}\frac{x^{2}\sin1/x}{\sin x}\] is
a) 1
b) 0
c) 1/2
d) None of these
Explanation:

10. The value of \[\alpha\] so that \[\lim_{x \rightarrow 0}\frac{1}{x^{2}}\left(e^{\alpha x}-e^{x}-x\right)=\frac{3}{2}\] is
a) 0
b) 1
c) 4
d) 2
Explanation: