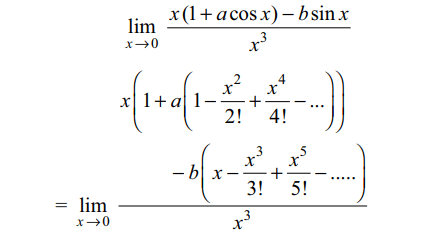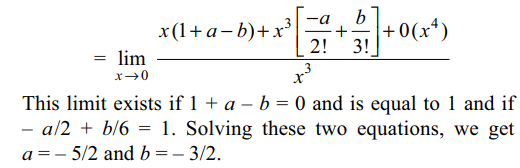1.Let \[f\left(x\right)=\lim_{n \rightarrow \infty} \frac{x^{2n}-1}{x^{2n}+1}\] , then
a) f(x)=1 for \[\mid x \mid>1\]
b) f(x)=-1 for \[ \mid x \mid<1\]
c) f(x) is not defined for any value of x
d) Both a and b
Explanation:
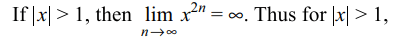
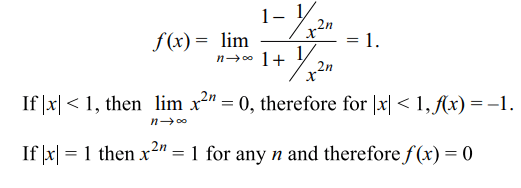
2. If \[\lim_{x \rightarrow 0}\frac{a\sin x-bx+cx^{2}+x^{3}}{2x^{2}\log\left(1+x\right)-2x^{3}+x^{4}}\] exist and is finite , then
a) a = b
b) c = 0
c) a = b
d) All of the Above
Explanation:
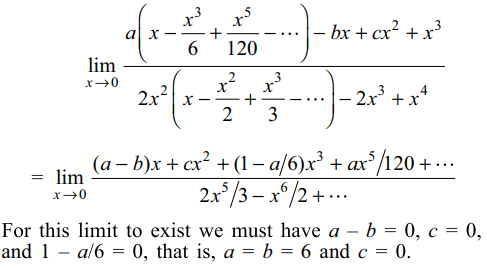
3. if \[\lim_{x \rightarrow 0}\frac{ae^{x}-b \cos x+ce^{-x}}{x \sin x}=2\] then
a) a = b
b) c = 1
c) b = 2
d) All of the Above
Explanation:
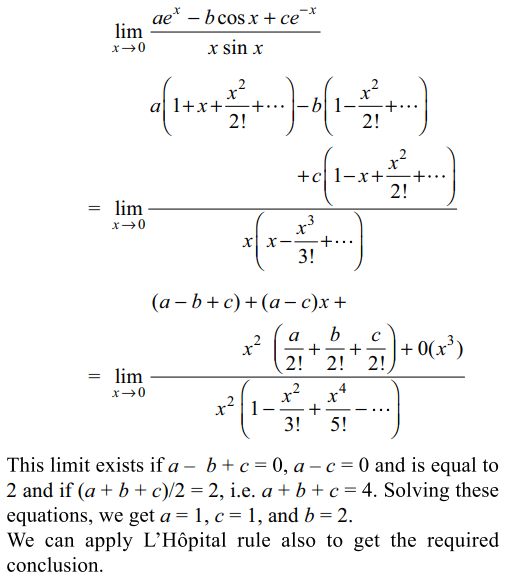
4. A function f (x) is defined by \[f\left(x\right)=\frac{\left[x^{2}\right]-1}{x^{2}-1}\] for \[x^{2}\neq 1,\] f(1)= f(-1) = 0 , then
a) \[\lim_{x \rightarrow 1+}f\left(x\right) =0\]
b) \[\lim_{x \rightarrow 1}f\left(x\right) \] does n't exist
c) \[\lim_{x \rightarrow 1-}f\left(x\right) \] does n't exist
d) All of the Above
Explanation:
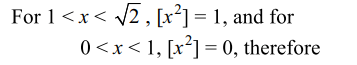
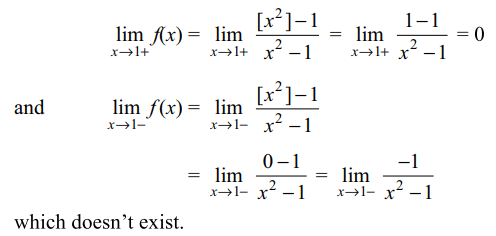
5. If \[f\left(x\right)=\begin{cases}\frac{ae^{1/\mid x+2\mid}-1}{2-e^{1/\mid x+2\mid}} &-3< x < -2 \\b&\ x=-2 \\\sin\left(\frac{x^{4}-16}{x^{5}+32}\right) &\ -2< x< 0 \end{cases}\]
is continuous at x = - 2 , then
a) b = - a
b) \[b = -\sin 2/5\]
c) \[a = \sin 2/5\]
d) All of the Above
Explanation:
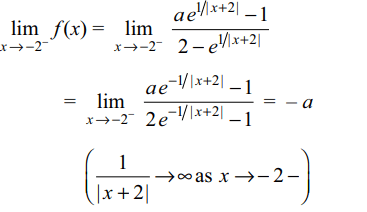
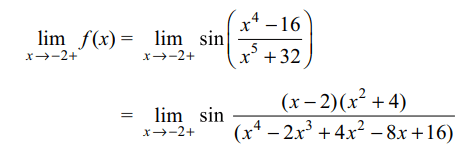

6. If \[f\left(x\right)=\frac{\sin 3x+Asin 2x + Bsin x }{x^{5}}\]
for \[ x\neq 0\] is continuous at x = 0 , then
a) \[f\left(0\right)=1\]
b) A = 4
c) A = -4
d) Both a and c
Explanation:

7. If \[A= \lim_{x \rightarrow -2}\frac{\tan \pi x}{x+2}+\lim_{x \rightarrow \infty}\left(1+\frac{1}{x^{2}}\right)^{x}\]
then
a) A > 3
b) A > 4
c) A is a transcedental number
d) All of the Above
Explanation:
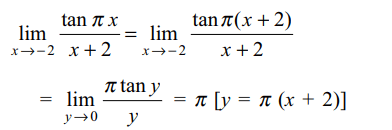
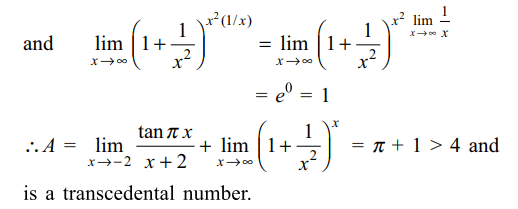
8. Let \[f\left(x\right)=\begin{cases}\frac{(1-\cos4x)\tan x}{x^3} & if x < 0\\2a^{2}&\ if x = 0 \\\frac{\sqrt{x}}{\sqrt{16+\sqrt{x}}-4} &if x > 0 \end{cases}\]
The possible value of a so that f is a continuous is
a) 4
b) 2
c) -2
d) Both b and c
Explanation:
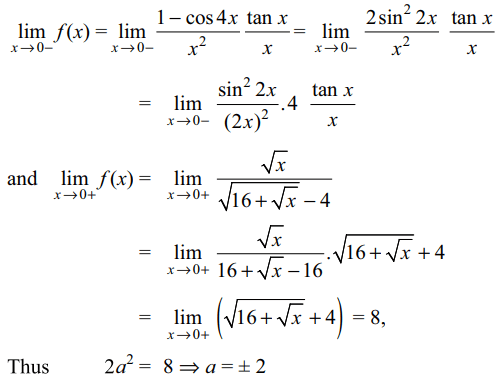
9. Let \[f\left(x\right)=\frac{\left(\log\left(1+x\right)-\log 2\right)\left(3.4^{x-1}-3x\right)}{\left\{\left(7+x\right)^{1/3}-\left(1+3x\right)^{1/2}\right\}\sin \pi x}, x\neq 1\]
The value of f(1) so that f is continuous at x = 1 is
a) an algebraic number
b) \[-\frac{9}{\pi}\log\frac{e}{4}\]
c) a transcedental number
d) Both b and c
Explanation:
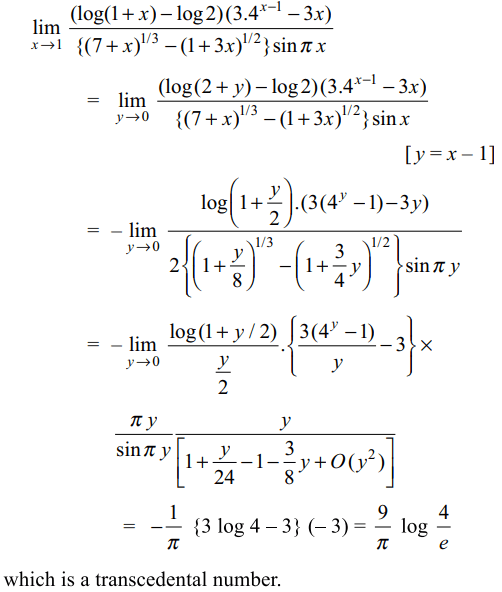
10. If \[\lim_{x \rightarrow 0}\frac{x\left(1+a\cos x\right)-b\sin x}{x^{3}}=1,\] then
a) b - a = 5/6
b) a =- 5/2
c) a - b = -1
d) Both b and c
Explanation: