1. Let f be a continuous function on satisfying
f (x + y) = f(x) + f(y) for all x, \[y \epsilon R\] and
f(1) = 5 then \[\lim_{x \rightarrow 4}f\left(x\right)\] is equal to
a) 4
b) 80
c) 0
d) None of these
Explanation:
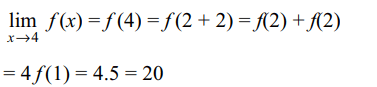
2. Let \[f\left(x\right)=e^{x} sgn\left(x+\left[x\right]\right)\] , where sgn is the signum
function and [x] is the greatest integer function.
Then
a) \[\lim_{x \rightarrow 0+}f\left(x\right)=0\]
b) \[\lim_{x \rightarrow 0+}f\left(x\right)=-1\]
c) \[\lim_{x \rightarrow 0+}f\left(x\right)=1\]
d) \[\lim_{x \rightarrow 0+}f\left(x\right)=2\]
Explanation:
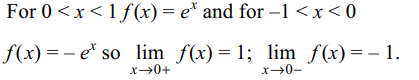
3. Let \[f\left(x\right)=\begin{cases}\frac{x^{2}+2\cos x-2}{x^{4}}, & x < 0\\\frac{\sin x-\log\left(e^{x}\cos x\right)}{6x^{2}}, & x > 0\end{cases}\]
The value of f(0), so that f is continuous is
a) \[\frac{1}{5}\]
b) \[\frac{1}{3}\]
c) \[\frac{1}{12}\]
d) \[\frac{1}{6}\]
Explanation:

4. If \[f\left(x\right)=x\left(e^{1/x}-1\right)\] , then \[\lim_{x \rightarrow \infty}f\left(x\right)\] is
a) -1
b) 1
c) 0
d) none of these
Explanation:
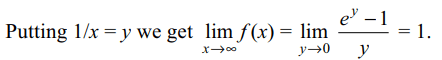
5. The value of f(0) so that the function \[f\left(x\right)=\frac{1-\cos\left(1-\cos x\right)}{x^{4}}\]
is continuous everywhere is
a) 1/8
b) 1/2
c) 1/4
d) none of these
Explanation:
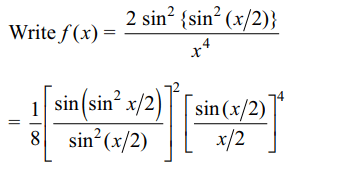
6. The function \[f\left(x\right)=\frac{\log\left(1+ax\right)-\log\left(1-bx\right)}{x}\]
is not defined at x = 0. The value which should be
assigned to f at x = 0 so that it is continuous there, is
a) a- b
b) a +b
c) log a + log b
d) none of these
Explanation:

7. The function \[f\left(x\right)=\frac{1+\sin x-\cos x}{1-\sin x-\cos x }\]
is not defined at x = 0. The value of f (0) so that f (x)
is continuous at x = 0, is
a) 1
b) -1
c) 0
d) none of these
Explanation:
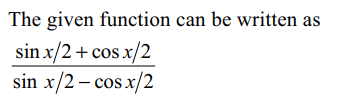
8. The function \[f\left(x\right)=\frac{\cos x-\sin x}{\cos 2x }\]
is not defined at \[ x=\pi/4\] . The value of \[ f\left(\pi/4\right)\] so
that f(x) is continuous everywhere, is
a) 1
b) -1
c) \[\sqrt{2}\]
d) \[1/\sqrt{2}\]
Explanation:
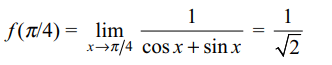
9. The value of f(0), for \[f\left(x\right)=\left(1+\tan^{2}\sqrt{x}\right)^{1/2x}\] , so
that f(x) is continuous everywhere, is
a) e
b) 1/2
c) \[e^{1/2}\]
d) 0
Explanation:
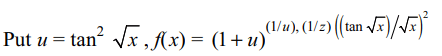
10. The value of \[\lim_{x \rightarrow 0}\frac{\left(1+x\right)^{1/4}-\left(1-x\right)^{1/4}}{x}\] is
a) 1/2
b) 0
c) -1
d) -1/2
Explanation:
