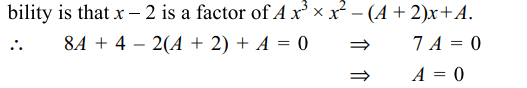1. \[\lim_{x \rightarrow0}\frac{\sin^{-1}x-\tan^{-1}x}{x^{3}}\] is equal to
a) 2
b) 1
c) -1
d) 1/2
Explanation:

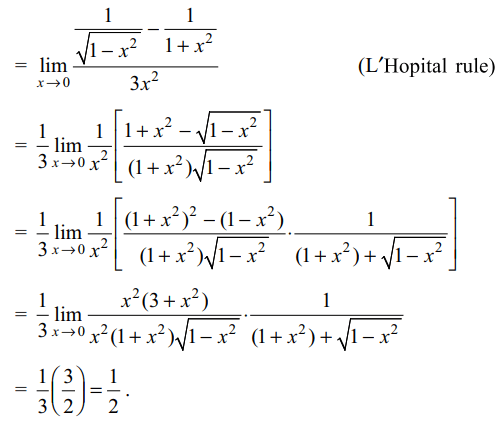
2. \[\lim_{x \rightarrow0}\frac{e^{x^{2}}-\cos x}{x^{2}}\] is equal to
a) 3/2
b) 1/2
c) 2/3
d) none of these
Explanation:
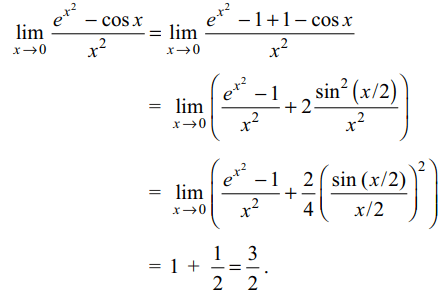
3. \[\lim_{x \rightarrow-1+}\frac{\sqrt{\pi}-\sqrt{\cos^{-1}x}}{\sqrt{x+1}}\] is equal to
a) \[1/\sqrt{2}\]
b) \[1/\sqrt{2\pi}\]
c) \[1/\sqrt{\pi}\]
d) none of these
Explanation:

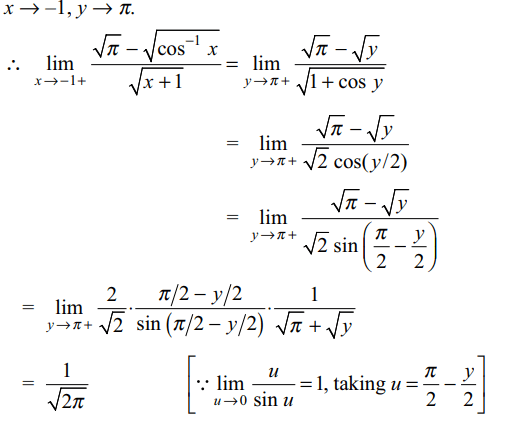
4. The value of f(0) so that the function \[f\left(x\right)=\frac{\cos\left(\sin x\right)-\cos x}{x^{4}}\] is continuous at each point in its domains , is equal to
a) 2
b) 1/6
c) 2/3
d) -1/3
Explanation: For f to be continuous, we must have

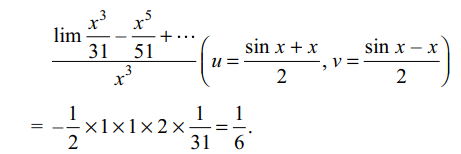
5. Let f(x) =\[\begin{cases}-2\sin x & if & x\leq-\pi/2 \\A\sin x+B & if & -\pi/2 < x<\pi/2\\\cos x & if & x\geq\pi/2\end{cases}\]
The values of A and B so that f(x) is continuous every where are
a) A = 0 ,B = 1
b) A = 1 ,B = 1
c) A = -1 ,B = 1
d) A = -1 ,B = 0
Explanation: Since sin x and cos x are continuous functions,
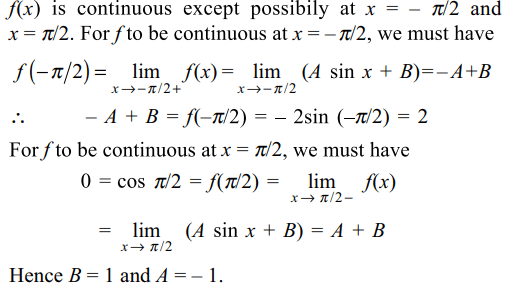
6. Let \[f\left(x\right)=\frac{\tan\left[e^{2}\right]x^{3}-\tan\left[-e^{2}\right]x^{3}}{\sin^{3}x},x\neq0\]
The value of f(0) for which f(x) is continuous is
a) 15
b) 12
c) -12
d) 14
Explanation:
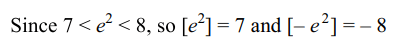
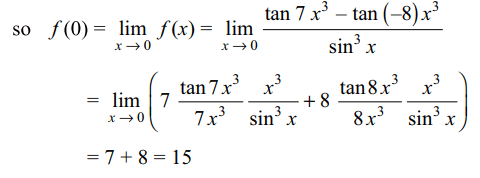
7. The value of f(0) so that the function \[f\left(x\right)=\frac{\sqrt{1+x}-\sqrt[3]{1+x}}{x}\]
becomes continuous, is equal to
a) 1/6
b) 1/4
c) 2
d) 1/3
Explanation: The function f(x) is continuous except possibly

8. Let \[f\left(x\right)=\left(2-\frac{x}{a}\right)^{\tan\left(\frac{\pi x}{2a}\right)},x\neq a\]
The value which should be assigned to f at x = a so that it is continuous everywhere is
a) \[2/\pi\]
b) \[e^{-2/\pi}\]
c) 2
d) \[e^{2/\pi}\]
Explanation: For f to be continuous, we must have
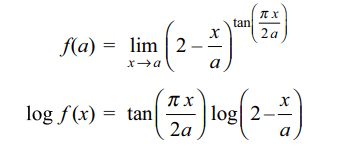
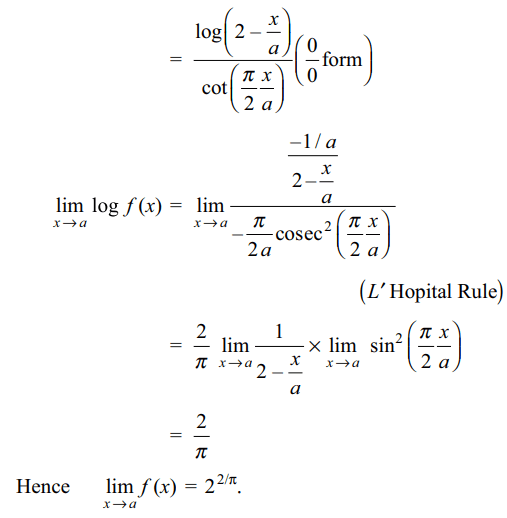
9. Let \[f\left(x\right)=\begin{cases}\left(\frac{e^{-x}+x^{2}-1}{-x}\right)^{\frac{-1}{x}} & -1\leq x < 0\\\frac{e^{1/x}+e^{2/x}+e^{3/\mid x \mid}}{ae^{2/x}+be^{3/\mid x \mid}} & 0< x< 1\end{cases}\]
The value of b so that \[\lim_{x\rightarrow 0}f\left(x\right)\] exist is
a) \[e^{1/2}\]
b) \[e^{3/2}\]
c) \[e^{-3/2}\]
d) \[e^{2}\]
Explanation:

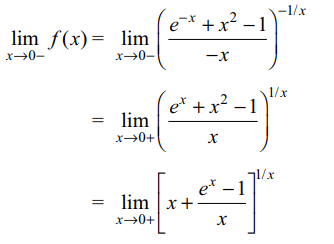
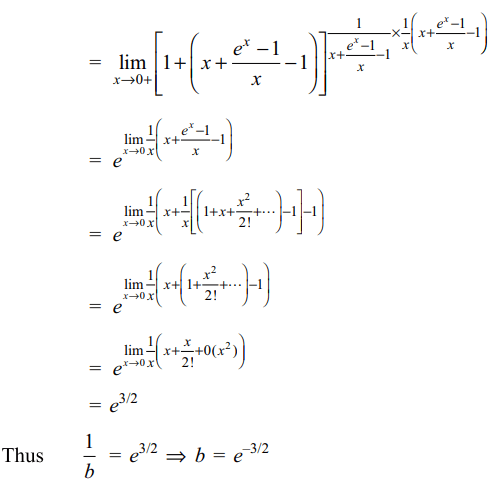
10. If the function \[f\left(x\right)=\begin{cases}\frac{Ax^{3}+x^{2}-\left(A+2\right)x+A}{x-2} & x \neq 2\\2 & x=2 \end{cases}\]
is continuous at x=2 , then
a) A = 0
b) A = 1
c) A = -1
d) none of these
Explanation: Since f is continuous at x = 2, the only possible