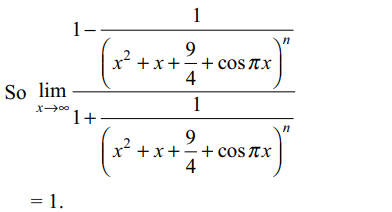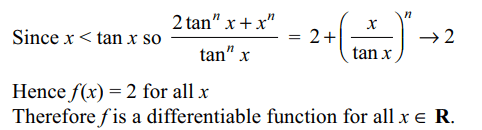1. Let \[f\left(x\right)=\begin{cases}x^{2} & if x\leq x_{0}\\ax+b & if x>x_{0} \end{cases}\]
The value of the coefficients a and b for which the
function is continuous and has a derivative at \[x_{0}\] , are
a) \[a=x_{0}, b=-x_{0}\]
b) \[a=2x_{0}, b=-x_0^2\]
c) \[a=x_0^2, b=-x_{0}\]
d) \[a=x_{0}, b=-x_0^2\]
Explanation: For f to be continuous everywhere, we must have
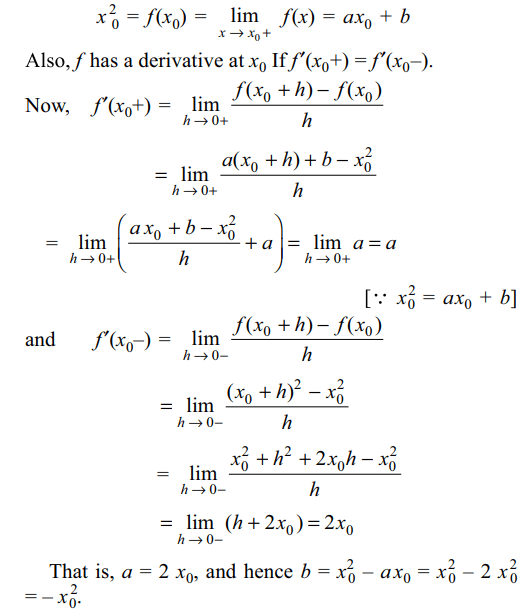
2. Given f' (2) = 6 and f' (1) = 4,
\[\lim_{h \rightarrow 0}\frac{f\left(2h+2+h^{2}\right)-f\left(2\right)}{f\left(h-h^{2}+1\right)-f\left(1\right)}\]
is equal to
a) 3/2
b) 3
c) 5/2
d) -3
Explanation:
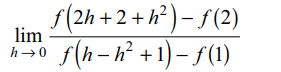
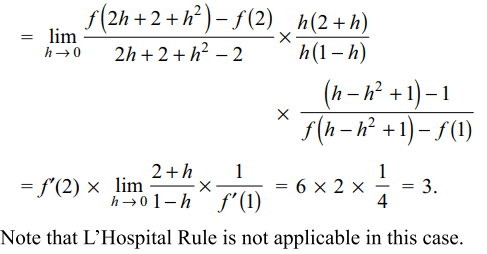
3. Let \[f:R\rightarrow R\] be such that f (1) = 3 and
f' (1) = 6. Then \[\lim_{x \rightarrow 0}\left(\frac{f\left(1+x\right)}{f\left(1\right)}\right)^{1/x}\] equals
a) 1
b) \[e^{1/2}\]
c) \[e^{2}\]
d) \[e^{3}\]
Explanation:
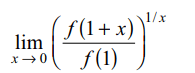
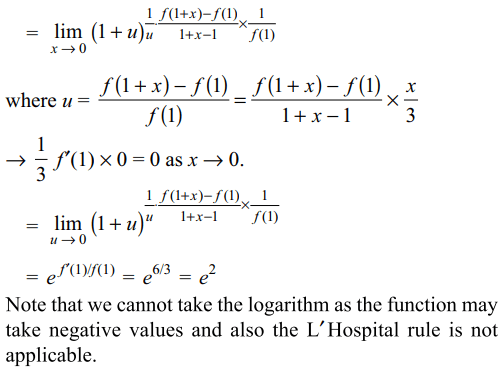
4.The domain of the derivative of the function \[f\left(x\right)=\begin{cases}\tan^{-1}x &\mid x\mid \leq1\\\frac{1}{2}\left(\mid x\mid-1\right) & \mid x\mid > 1\end{cases}\]
a) \[R \sim\left\{0\right\}\]
b) \[R \sim\left\{1\right\}\]
c) \[R \sim\left\{-1\right\}\]
d) \[R \sim\left\{-1,1\right\}\]
Explanation:

5. If f (1) = 1, f' (1) = 3 then the derivative of
y = f (f ( f ( f (x))) at x = 1 is
a) 256
b) 16
c) 81
d) 27
Explanation: y'(x) = f'(f(f(f(x))) f'(f(f(x))) f'( f(x)) f'(x)
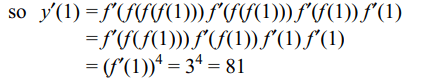
6. \[f\left(x\right)=\begin{cases}ax & x < 2\\ax^{2}-bx+3 & x \geq 2\end{cases}\]
If f is differentiable for all x then
a) a = 3/4, b = 9/4
b) a = 1, b = 2
c) a = 3/2, b = 9/2
d) a = 3/4, b = 9/2
Explanation: Since f is differentiable for all x, in particular
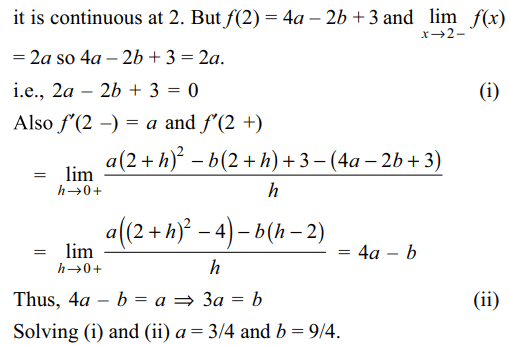
7. Let f and g be differentiable function such
that f' (x) = 2g(x) and g' (x) = – f (x), and let \[T\left(x\right)=\left(f\left(x\right)\right)^{2}-\left(g\left(x\right)\right)^{2}.\]
Then T' (x) is equal to
a) T(x)
b) 0
c) 2f (x) g(x)
d) 6 f (x) g(x)
Explanation:

8. Let f be a twice differentiable function
such that f" (x) = – f (x) and f' (x) = g(x). If \[h'\left(x\right)=\left[f\left(x\right)\right]^{2}+\left[g\left(x\right)\right]^{2}\] , h(1) = 7 and h(0) = 2, then h(3) is equal to
a) 11
b) 4
c) 14
d) 13
Explanation:

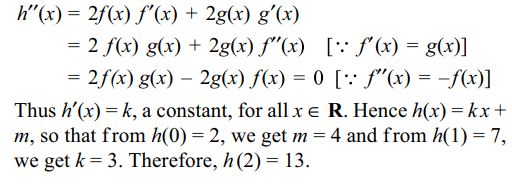
9. If \[y^{2}=P\left(x\right)\] is a polynomial of degree 3,
\[2\frac{d}{dx}\left(y^{3}\frac{d^{2}y}{dx^{2}}\right)\] is equal to
a) P(x) + P'(x)
b) P(x) P'(x)
c) P(x) P'''(x)
d) a constant
Explanation: From y2 = P(x), we have 2yy1 = P'(x), i.e.,
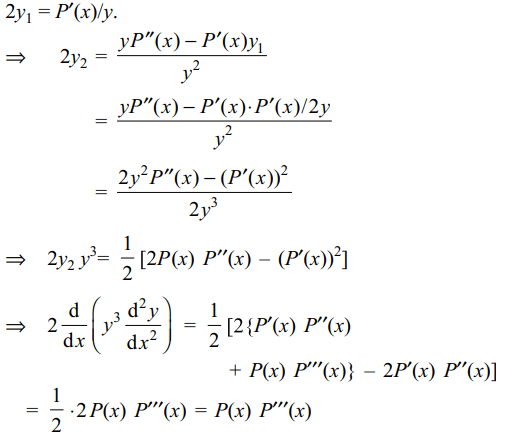
10. Let \[f\left(x\right)=\lim_{n \rightarrow \infty}\frac{\left(x^{2}+x+\frac{9}{4}+\cos\pi x\right)^{n}-1}{\left(x^{2}+x+\frac{9}{4}+\cos\pi x\right)^{n}+1}.\left(\frac{2\tan ^{n}x+x^{n}}{\tan^{n}x}\right)\]
then
a) f is differentiable for all \[x\epsilon R\]
b) f is continuous but not differentiable
c) f is discontinuous at all \[n\epsilon I\]
d) f is discontinuous only at finitely many points
Explanation: