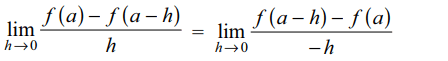PrepBharat

1. Let \[f\left(x\right)=\begin{cases}x^{3} \mid \cos\frac{\pi}{2x}\mid& x \neq 0\\+x^{4}\mid\sin\frac{\pi}{x}\mid\\0, & x= 0\end{cases}\]
then f is
a) differentiable at x = 0 and x = 1
b) differentiable at x = 0 not differentiable at x = 2
c) differentiable at x = 2 and not differentiable at x = 1
d) differentiable neither at x = 0 nor at x = 2.

View Answer

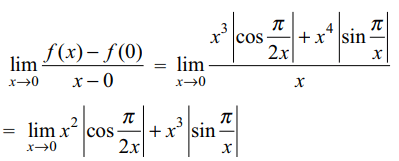
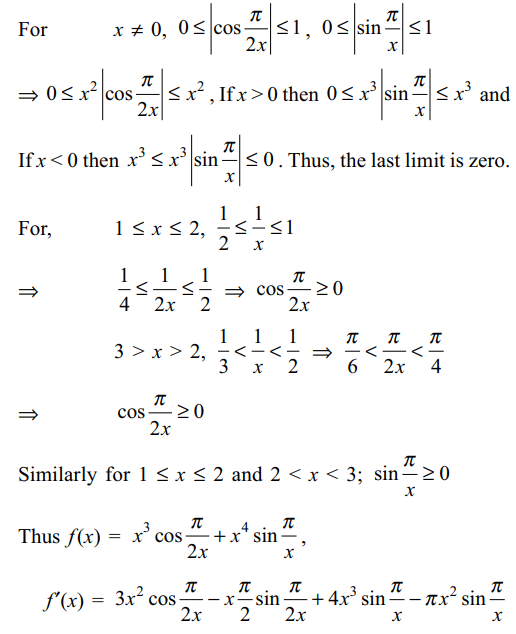
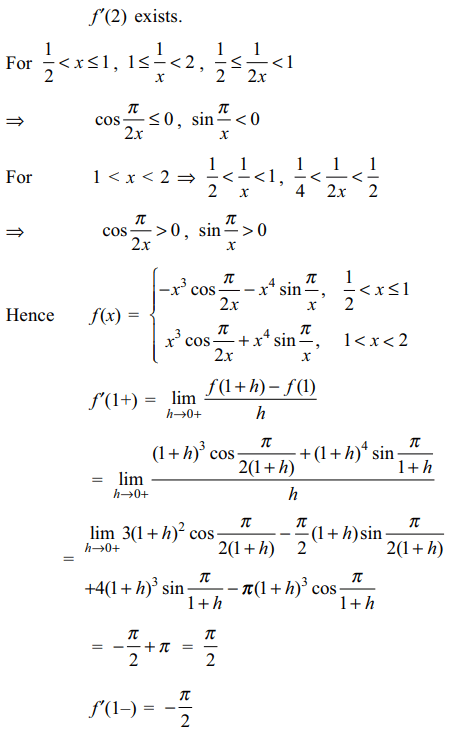
2. If \[f\left(x\right)=\cot^{-1}\left(\frac{x^{x}-x^{-x}}{2}\right)\]     then f' (1) equals
a) -1
b) 1
c) log 2
d) – log 2.

View Answer

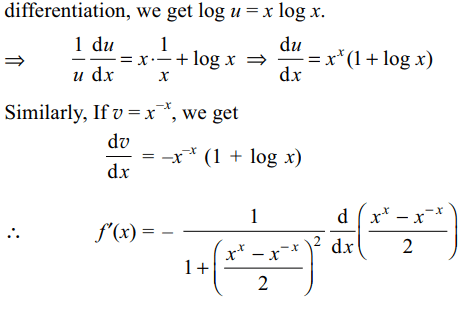
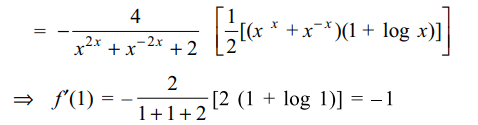
3. If \[f\left(x\right)=\left(1+x\right)^{n}\]   , then the value of \[f\left(0\right)+f'\left(0\right)+\frac{f"\left(0\right)}{2!}+....+\frac{\left(0\right)}{}\]       is
a) n
b) \[2^{n}\]
c) \[2^{n+1}\]
d) none of these

View Answer

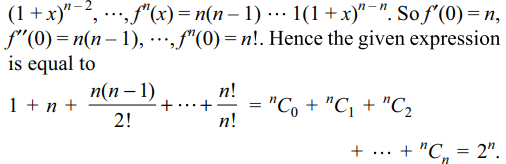
4. The solution set of f '(x) > g'(x) where \[f\left(x\right)=\left(1/2\right)5^{2x+1}\]     and \[g\left(x\right)=5^{x}+4x\log 5\]     is
a) \[\left(1,\infty\right)\]
b) \[\left(0,1\right)\]
c) \[\left[0,\infty\right)\]
d) \[\left(0,\infty\right)\]

View Answer

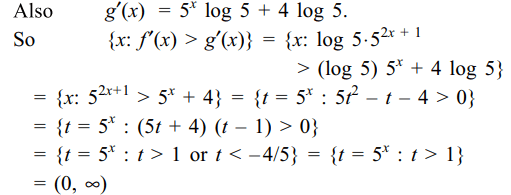
5.Let \[f\left(x\right)=\sin x;g\left(x\right)=x^{2}\]     and h(x) = log x. If u (x) = h( f (g(x))), then \[\frac{d^{2}u}{dx^{2}}\mid x=\sqrt{\pi}/2\]     is
a) \[2-\pi\]
b) \[2-2\pi\]
c) \[\pi-2\]
d) \[2\pi-2\]

View Answer

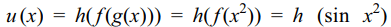
6. If \[y=\tan^{-1}\frac{1}{1+x+x^{2}}+\tan^{-1}\frac{1}{x^{2}+3x+3}+\tan^{-1}\frac{1}{x^{2}+5x+7}+....+\]
up to n terms, then y'(0) is equal to
a) \[-\frac{1}{1+n^{2}}\]
b) \[-\frac{n^{2}}{1+n^{2}}\]
c) \[\frac{n}{1+n^{2}}\]
d) none of these

View Answer

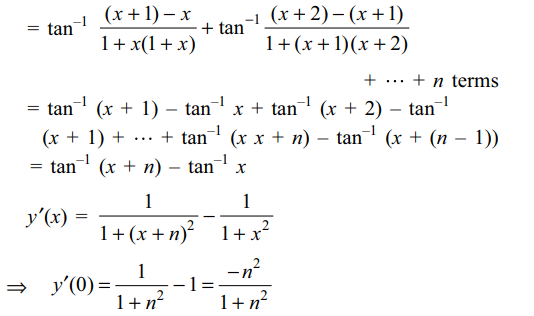
7. Let f and g be functions satisfying
\[f\left(x\right)=e^{x}g\left(x\right),f\left(x+y\right)=f\left(x\right)+f\left(y\right),g\left(0\right)=0 , g'\left(0\right)=4\]
g and g' are continuous at 0. Then
a) f (x) = 0 for all x
b) f (x) = x for all x
c) f (x) = x + 4 for all x
d) f (x) = 4 x for all x

View Answer

8. Let \[f:R\rightarrow R\]   is a function which is defined by \[f\left(x\right)=\max\left\{x,x^{3}\right\}\]    . The set of all points on which f (x) is not differentiable is
a) \[\left\{-1,1\right\}\]
b) \[\left\{-1,0\right\}\]
c) \[\left\{0,1\right\}\]
d) \[\left\{-1,0\right\}\]

View Answer

9. Which of the following functions is differentiable at x = 0?
a) cos (|x|) + |x|
b) cos (|x|) – |x|
c) sin |x| + |x|
d) sin (|x|) – |x|

View Answer

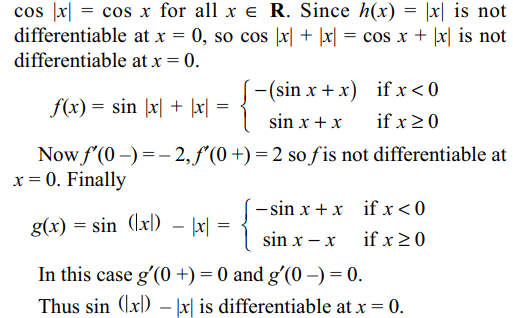
10. If f is a differentiable function at a point 'a’ and \[f'\left(a\right)\neq0\]   then which of the following is true.
a) \[-f'\left(a\right)=\lim_{h \rightarrow 0}\frac{f\left(a\right)-f\left(a-h\right)}{h}\]
b) \[\frac{1}{2}f'\left(a\right)=\lim_{h \rightarrow 0}\frac{f\left(a+2h\right)-f\left(a+h\right)}{2h}\]
c) \[f'\left(a\right)=\lim_{h \rightarrow 0}\frac{f\left(a+2h\right)-f\left(a\right)}{h}\]
d) \[3f'\left(a\right)=\lim_{h \rightarrow \infty}\frac{f\left(a+3h\right)-f\left(a+h\right)}{h}\]

View Answer