1. Let f be a differentiable function on R taking non negative values such that \[\lim_{x \rightarrow 0}\frac{f'\left(x\right)}{x}\] exists and satisfy
\[f\left(x\right)f\left(y\right)=f\left(x_{1}\right)f\left(y_{1}\right)\]
For all \[x,y,x_{1},y_{1}\] such that \[x^{2}+y^{2}=x_1^2+y_1^2\] such that
f (0) = 1, then
a) f is infinitely many times differentiable
b) f is an exponetial function
c) \[\lim_{x \rightarrow 0}f\left(x\right)=1\]
d) All of the Above
Explanation: Taking logarithm of both sides,
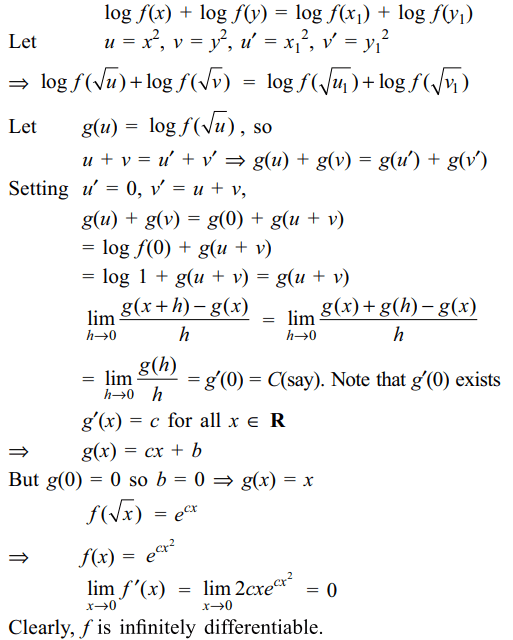
2. Let [x] denote the greatest integer less than or equal to x.
If \[f\left(x\right)=\left[x\sin\pi x\right]\] , then f (x) is
a) continuous at x = 0
b) continuous in (–1, 0)
c) differentiable in (– 1, 1)
d) All of the Above
Explanation: By definition of [x], we have f(x) = [x sin \[\pi\] x]
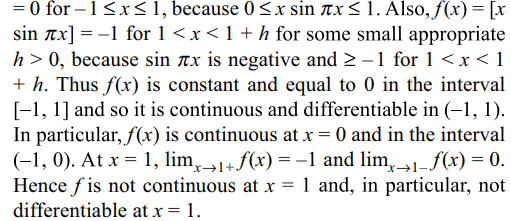
3. The function \[f\left(x\right)=\begin{cases}\mid x-3 \mid& x \geq 1\\\frac{x^{2}}{4}-\frac{3x}{2}+\frac{13}{4} & x < 1\end{cases}\]
is
a) continuous at x = 1
b) continuous at x = 3
c) differentiable at x = 1
d) All of the Above
Explanation: The given function can be written as

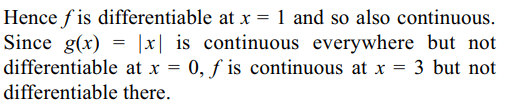
4. If \[f\left(x\right)=\begin{bmatrix}x^{n} &\sin x & -\cos x \\n! &\sin\left(n\pi/2\right)& \cos\left(n\pi/2\right)\\a &a^{2} & a^{3} \end{bmatrix}\]
the value of \[\frac{d^{n}}{dx^{n}}\left(f\left(x\right)\right)\] at x = 0 for n = 2m + 1 is
a) independent of a
b) 0
c) \[a^{6}\]
d) Both a and b
Explanation:

5. If \[f\left(x\right)=\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}\]
then
a) f is a differentiable at all points of its domain except x= 4
b) f is differentiable on \[\left(2,\infty\right)\sim\left\{4\right\}\]
c) f' (x) = 0 for all \[x\epsilon\] [2,4)
d) All of the Above
Explanation:
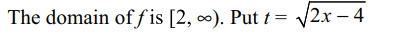
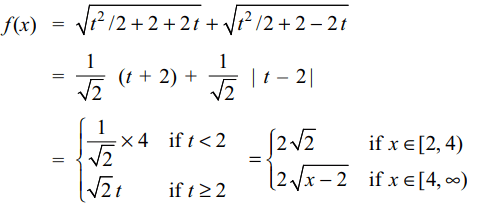
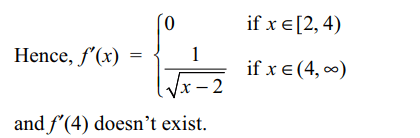
6. If f'(5) = 4 then \[\lim_{x \rightarrow \infty}\frac{f\left(5+h^{2}\right)-f\left(5-h^{2}\right)}{2h^{2}}\]
is
a) 2
b) 4
c) 3
d) 1/4
Explanation:
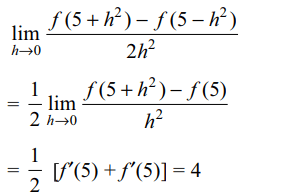
7. If \[y=\tan^{-1}\left(\frac{\log ex^{-3}}{\log ex^{3}}\right)+\tan^{-1}\left(\frac{3+3\log x}{1-9\log x}\right)\]
then \[\frac{d^{2} y}{dx^{2}}\] is
a) 2
b) 1
c) 0
d) -1
Explanation:
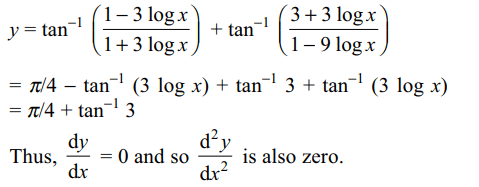
8. If \[f\left(x\right)=\frac{\tan x+\sec x -1}{\tan x-\sec x+1}\] then \[f'\left(\pi/4\right)\] is equal to
a) \[\sqrt{2}\left(\sqrt{2}-1\right)\]
b) \[\sqrt{2}+1\]
c) \[\sqrt{2}\left(\sqrt{2}+1\right)\]
d) \[\sqrt{2}-1\]
Explanation:
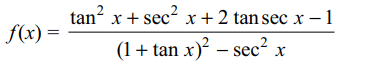
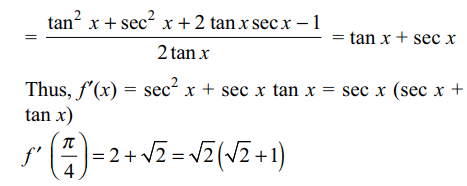
9. If \[f\left(x\right)=x^{1/x}\] then f'' (e) is equal to
a) \[e^{1/\left({e-3}\right)}\]
b) \[e^{1/e}\]
c) \[e^{1/\left({e-2}\right)}\]
d) \[e^{1/e-3}\]
Explanation:

10. If \[y=f\left(\frac{3x+4}{5x+6}\right)\] and \[f"\left(x\right)=\tan x^{2}\] then \[\frac{dy}{dx}\] is
equal to
a) \[-2\tan\left(\frac{3x+4}{5x+6}\right)^{2}\times\frac{1}{\left(5x+6\right)^{2}}\]
b) \[f\left(\frac{3\tan x^{2}+3}{5\tan x^{2}+6}\right) \tan x^{2}\]
c) \[ \tan x^{2}\]
d) \[ \tan \left(\frac{3x+4}{5x+6}\right)^{2}\]
Explanation:
